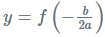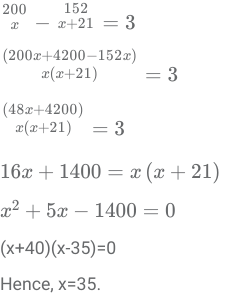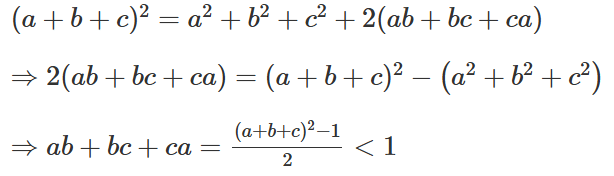Overview: Quadratic Equations | Quantitative Aptitude (Quant) - CAT PDF Download
Introduction
- Quadratic equations are the basics of algebra and one must be familiar with them to be able to score well in the algebra section of competitive exams like CAT and MAT.
- A clear understanding of the core concepts of quadratic equations would create a clear framework in your mind about how to solve these equations.
- Once the basics are clear, quadratic equations become very easy to work with.
What are Quadratic Equations?
- The equation ax2 + bx + c = 0 is the general or standard form of quadratic equation. For example: x2 +5x + 12 = 0 and 5x2 −4x − 16 = 0 are quadratic equations in the variable x.
‘a’ denotes the coefficient of x2.
‘b’ denotes the coefficient of x.
‘c’ is the constant. - You must simplify a given equation before deciding whether it is quadratic or not.
- In the equation above ‘a’ is termed the leading coefficient and ‘c’ is named the absolute term of f (x). The values of x that satisfy the quadratic equation are called the roots of the quadratic equation (denoted by;α,β).
Roots of a Quadratic Equation
- Quadratic equations have exactly two roots (solutions), resulting in the following cases:
Case 1: Both the roots are real and equal
Case 2: Both the roots are real and unequal
Case 3: Both the roots are imaginary - These are also identified as polynomial equations of degree 2 (due to the presence of x2) in one variable. The important formula for quadratic equations in determining the roots is:
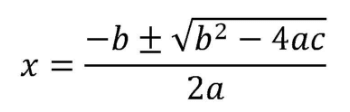
- The quadratic equation in mathematics will always possess two roots and the nature of roots may be either real or imaginary depending upon the equation. Always remember that quadratic equations are second-degree polynomial i.e if a given equation appears to be a third-degree equation that is not quadratic. You will learn more about the above formula in the coming headings.
Nature of Roots of Quadratic Equation
Now that you know what the roots of a given quadratic equation are and how to find them. Let us step forward and learn about the nature of the root and how to find the nature of the roots of a quadratic equation.
The nature of the roots can be found by finding the roots using the formula. Another approach to determining nature is to find the value of b2–4ac. Here, b2–4ac is the part of the formula used to solve a quadratic equation. Let us understand how the nature of roots depends on this equation.
The general formula to obtain the roots is 
- If b2 – 4ac = 0, then the nature of the roots α and β are real and equal.
- If b2 − 4ac < 0, then the roots α and β are not real or the roots are imaginary.
- If b2− 4ac > 0 then the nature of the roots α and β are real and different/unequal.
- If b2 −4ac > 0 + a perfect square then the roots α and β are real, rational and unequal.
- If b2 − 4ac > 0 + not a perfect square, then the roots α and β are real, irrational and unequal.
What is Discriminant?
To compose the standard form of a quadratic equation, the x2 term is penned first, followed by the x term, and eventually, the constant term is written. The value b2–4ac denotes the discriminant of a quadratic equation and is expressed by the symbol ‘D’.
- If D > 0, the roots obtained are real and unequal.
- If D = 0, the roots fetched are real and equal.
- If D < 0, existing roots are imaginary and unequal.
Relationship between Coefficient and Roots of Quadratic Equation
- For the quadratic equation ax2 + bx + c = 0 , the terms a,b and c specify the coefficient of x2, x, and the constant term respectively. On the other hand, the roots of a quadratic equation are denoted by the symbols alpha (α), and beta (β). Now is there any relationship between the coefficient and roots of a quadratic equation? The answer would be yes.
- The sum and product of roots of a quadratic equation, can be computed using these coefficients as shown:
=> The sum of the roots 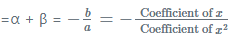
=> The product of roots of quadratic equation 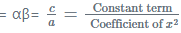
=> Also, if α and β, are the roots, then the quadratic equation can be formed using these roots. The equation is as follows: x2 –(α + β)x + (αβ) = 0
How to Solve Quadratic Equations?
Now that you know what a quadratic equation is with the definition and formula for solving such questions followed by information on the roots, their nature and roots of the quadratic equation formula. Let us now understand the different methods of solving quadratic equations.
1. Factorizing Quadratic Equation
Factoring quadratic equations is an approach where the equation ax2 + bx + c = 0is factorised as (x – ∝)(x – β) = 0 and then equation is solved to get x = ∝ or x = β. A standard form of quadratic equation in one variable can be solved by factorising the equation, i.e., by making factors out of the equation.
Consider the equation x2 −7x + 12 = 0 , it can also be written as (x-3)(x-4)=0. Now this factorised equation can be very easily solved using a property of real numbers called the zero-product rule. We will cover the detailed procedure in the separate article.
2. Formula Method of Finding Roots
Another approach for finding the roots is using the formula to find the roots of a quadratic equation. That is, solving the equation using the Sridharacharya formula. This can be a tricky method in terms of calculations but it is comparatively faster. This approach is generally used when the solution cannot be obtained using the factorisation method. Here the roots for the standard equation are obtained using the below formula: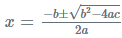
Using the above formula you will get two roots of x one with a positive sign and the other with a negative sign as shown below: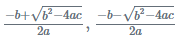
3. Method of Completing the Square
- In this method, you will learn how to find the roots of quadratic equations by the method of completing the squares. The steps involved in solving are:
For the equation; ax2 + bx + c = 0 - First, divide all terms of the equation by the coefficient of x2 i.e by ‘a’.
- The equation becomes:
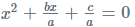
- Next, keep the terms of x2 and x on one side and shift the term c/a to the right side of the equation; x
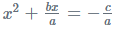
- Moreover, complete the square on the left side of the equation and counterbalance this by adding the identical value to the right.
- An equation similar to (x+s)2 = w is obtained.
- In the next step, take the square root for both sides of the equation.
- Lastly, shift the numeral present on the left side of the equation to the right side to find x.
4. Graphing Method to Find the Roots
Lastly, the solution can also be obtained by graphing quadratic equations. Consider the general form of a quadratic equation as a function of y, the equation becomes y = ax2 + bx + c
Next, substitute different values for x and obtain the respective values of y and plot the graph accordingly. The graph in general is a parabola-shaped graph for the quadratic equation.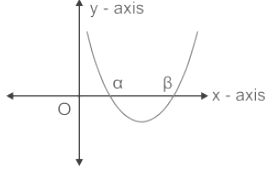
Quadratic Equations having Common Roots
For the given two quadratic equations a1x2 + b1x + c1 = 0 and a2x2 + b2x + c2 = 0. The condition for the two equations has a common root can be obtained as shown below.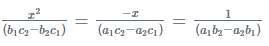
The above equations are obtained using the determinant method.
Solving the equation we get: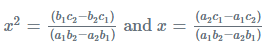
Now squaring x and equating with x2 we get;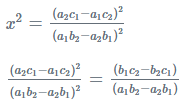
(a2c1 − a1c2)2 = (b1c2 − b2c1)(a1b2 − a2b1) is required condition for the equation to have one common root.
However, if both the roots of quadratic equations, a1x2 + b1x + c1 = 0 and a2x2 + b2x + c2 = 0 are common then: a1/a2 = b1/b2 = c1/c2
How to Solve Quadratic Equations with Common Roots?
In the previous heading, we saw the condition for a standard form of a quadratic equation to have one and two common roots. For a single common root the condition is;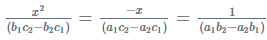 and for two common roots the condition is; a1/a2 = b1/b2 = c1/c2 . Let us now understand how to solve such equations having common roots with an example.
and for two common roots the condition is; a1/a2 = b1/b2 = c1/c2 . Let us now understand how to solve such equations having common roots with an example.
Example : For the given quadratic equation 4x2 + 24x + 6 = 0 and 7x2 – 6x + k = 0 what is the value of K for which the equations will have a common root?
Sol: (a2c1 − a1c2)2 = (b1c2 − b2c1)(a1b2 − a2b1) is required condition for the equation to have one common root.
Form the equation, a1 = 4, b1 = 24, c1 = 6, a2 = 7, b2 = -6 and c2 = k
Substituting the values in the equation we get:
[(24k)−(−6×6)]×[4(−6)−(7×24)]=(7×6−4k)2
[24k+36]×[−24−168]=(42−4k)2
−4608k−6912=1764−336k+16k2
16k2 + 4272k + 8676 = 0
Therefore, the values of k are -264.95, -2.04.
How to Find the Range of a Quadratic Equation?
- The general form of a quadratic function is represented by the equation y = ax2 + bx + c. As per the definition of the domain, it includes all the input values. Hence while determining the domain the concern of the graph is the horizontal axis, i.e. all the values of x. therefore, the domain is all real values.
- Now coming towards the range: The range of a function is the collection of all possible output values. This implies that while calculating the range the focus area is the vertical axis, that is, the values on the y axis. The value of the range also depends on the opening of the parabola. To identify whether the parabola opens upwards or downward, check for the sign of the coefficient of x2. If the sign of “a” is positive, then the parabola is concave upward and if “a” is negative, the parabola is concave downward.
- Also, if the parabola is concave upward, the range will have all the real values that are greater than or equal to;
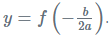 Similarly, if the parabola is concave downward, the range will have all the real values less than or equal to;
Similarly, if the parabola is concave downward, the range will have all the real values less than or equal to; 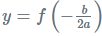
Example : Find the range of the quadratic function given by the equation y = x2 + 8x + 12
Sol: On comparing the standard equation with the given one.
y = ax2 + bx + c
We get a = 1, b = 8 and c = 12
As the coefficient of x2 i.e. “a” is positive, the parabola is concave upward. Hence the range will have all the real values that are greater than or equal to
x = -b / 2a
Substitute the values we get;
x = -8/2(12)
x = -8/24
x = -0.33
Substitute -0.33 for x in the given equation to obtain the y-coordinate at the vertex.
y=(−0.33)2 + 8(−0.33)+12
y = 0.1089 – 2.64+ 12
y = 9.46
Therefore, the y-coordinate of the vertex is 9.46.
As the parabola is concave upward, the range will have all the real values that are greater than or equal to 9.46.
Maximum and Minimum Value of Quadratic Equation
The minimum, as well as the maximum value of the quadratic equation, depends on the nature of the graph, i.e. whether the graph opens upwards or downwards. When the graph is concave upwards i.e. a>0 then the expression holds a minimum value at x = -b/2. On the other hand when the graph is concave downwards i.e. a<0 then the expression holds a maximum value at x = -b/2a
How to Find Maximum and Minimum values of Quadratic Functions?
In the previous heading, we use the two particular cases for the maximum and minimum values of the quadratic equations.
When the coefficient of x2 i.e. a > 0, the values lie in the ranges of [ f(-b/2a), ∞)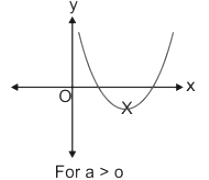 When the coefficient of x2 i.e. a < 0, the values lie in the ranges of (-∞, f(-b/2a)]
When the coefficient of x2 i.e. a < 0, the values lie in the ranges of (-∞, f(-b/2a)]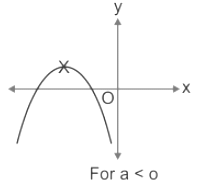
Example : Locate the maximum or minimum value of the given quadratic equation −9(x–3)2+3 ?
Sol: Given the equation; −9(x–3)2+3
Solving the equation we get:−9(x−3)2+3 = −9(x2 − 6x + 9) + 3 = −9x2 + 54x − 81 + 3
= −9x2 + 54x − 78
As, the coefficient of x2 is less than zero i.e. a < 0, the expression will hold a maximum value at x = -b/2a
By substituting the values we get, x=3
Therefore, the maximum value of the quadratic equation−9(x – 3)2+ 3 is 3.
Sign of a Quadratic Equation
- Let f(x)= y = ax2 + bx + c where a , b, c are real and a≠0 , then y = f(x) represents a parabola whose axis is parallel to y - axis.
- For some values of x, f(x) may be positive, negative or zero.
- Also, if a>0, the Parabola opens upwards
- If a<0, Parabola opens downwards.
Following cases are important from CAT and similar exam point of view. So go through them carefully , clearing your basics at the root level.
- a > 0 and D < 0 (Roots are imaginary)
→ The function will always be positive for all values of x. So, f(x)>0 and The graph will naturally not cut the X-axis.
- a > 0 and D = 0 ( Roots are real and identical)
→ f(x) will be positive for all values of x except at the vertex where f(x)= 0
→ So, f(x) ≥ 0 and graph touches the x-axis once.
- a > 0 and D > 0 ( Roots are real and distinct)
→ Let f(x) = 0 have two real roots α and β then f(x) will be positive for all real values of x which are lower than α or higher than β.
→ f(x) will be equal to zero when x is equal to either of α or β.
→ When x lies between α and β then f(x) will be negative.
→ The graph cuts the x - axis twice.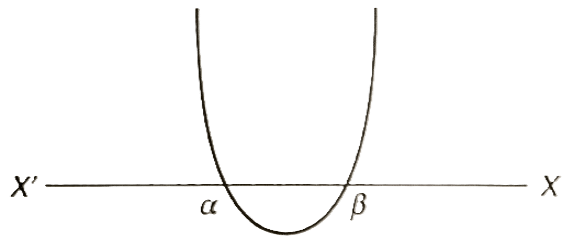
- a < 0 and D < 0 (Roots are Imaginary)
→ f(x) is negative for all values of x.
→ Mathematically, we can write f(x)<0 .
→ The graph will not touch or cut the x- axis.
- a < 0 and D = 0 ( Roots are real and equal)
→ f(x) is negative for all values of x except at the vertex where f(x) = 0
→ The graph touches the x-axis once.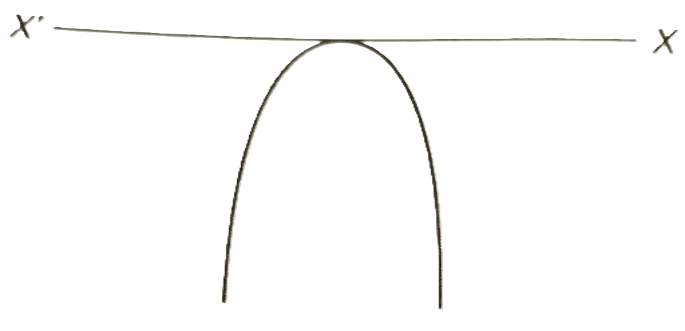
- a < 0 and D > 0
→Let f(x) = 0 have two roots α and β (α < β) then f(x) will be negative for all real values of x that are lower than α or higher than β.
→f(x) will be equal to 0 when x is equal either to α or to β.
→The graph cuts the x-axis twice.
Formulas for Solving Quadratic Equations
In the previous heading, we saw the formula to find the roots. Let us learn some other important formulas for quadratic equations for solving various types of questions in different examinations.
For a standard quadratic equation of the form ax2 + bx + c = 0.
- The roots are obtained by the formula:
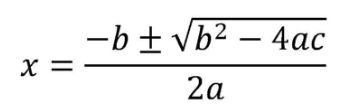
- The discriminant is calculated by the formula: b2 − 4ac
- If we consider α and β as the roots of a given quadratic equation then:
- The sum of roots of quadratic equation = S = α + β
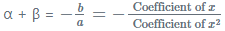
- The product of the roots = P = αβ
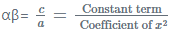
- The quadratic equation in the form of the above obtained roots: x2 –(α + β)x + (αβ) = 0
- For a cubic equation ax3 + bx2 + cx + d = 0, If α, β and γ are the roots then:
- Sum of the three roots = α+β+γ=−ba
- Product of the combination of two roots = αβ + βγ + λα = ca , and
- Product of all the three roots = αβγ = −da
Solved Examples
Example 1: Suppose hospital A admitted 21 less Covid infected patients than hospital B, and all eventually recovered. The sum of recovery days for patients in hospitals A and B were 200 and 152, respectively. If the average recovery days for patients admitted in hospital A was 3 more than the average in hospital B then the number admitted in hospital A was
Sol: Let the number of Covid patients in Hospitals A and B be x and x+21 respectively. Then, it has been given that:
A) a + b + 4 = 0
B) a + b − 4 = 0
C) a − b − 4 = 0
D) a − b + 4 = 0
Sol: Option 'a' is correct.Explanation: Let α,βα,β are roots of x2+bx+a=0x2+bx+a=0
Therefore α+β=−bα+β=−b and αβ=aαβ=a
again let γ,δγ,δ are roots of x2+ax+b=0x2+ax+b=0
Therefore γ+δ=−aγ+δ=−a and γδ=bγδ=b
Now given
α−β=γ−δα−β=γ−δ
⇒(α−β)2=(γ−δ)2⇒(α−β)2=(γ−δ)2
⇒(α+β)2−4αβ=(γ+δ)2−4γδ⇒(α+β)2−4αβ=(γ+δ)2−4γδ
⇒b2−4a=a2−4b⇒b2−4a=a2−4b
⇒b2−a2=−4(b−a)⇒b2−a2=−4(b−a)
⇒(b−a)(b+a+4)=0⇒(b−a)(b+a+4)=0
⇒b+a+4=0⇒b+a+4=0 as (a≠b)
A) less than 1
B) equal to 1
C) greater than 1
D) any real no
Sol :Option 'a' is correct.Explanation: In such type of problem if sum of the squares of number is known and we needed product of numbers taken two at a time or needed range of the product of numbers taken two at a time. We start square of the sum of the numbers like
B) 1
C) 3
D) 2
Sol: Option 'a' is correctExplanation: Given x2−3|x|+2=0x2−3|x|+2=0
If x≥0x≥0 i.e. |x|=x|x|=x
Therefore, the given equation can be written as
x2−3x+2=0x2−3x+2=0
⇒(x−1)(x−2)=0⇒(x−1)(x−2)=0
⇒x=1,2⇒x=1,2
Similarly for x<0,x2−3|x|+2=0x<0,x2−3|x|+2=0
⇒x2+3x+2=0⇒x2+3x+2=0
⇒x=−1, −2 ⇒x=−1, −2
Hence 1, −1, 2, −21, −1, 2, −2 are four solutions of the given equation.
B) 300
C) 400
D) None of these
Sol: Option 'b' is correct
Explanation: Let the optimum number of samosas be 200+20n
So, price of each samosa = (2-0.1*n)
Total price of all samosas = (2-0.1*n) * (200+20n)This quadratic equation attains a maximum at n = -20/2*(-2) = 5
So, the number of samosas to get the maximum revenue = 200 + 20*5 = 300
Example 6: Ujakar and Keshab attempted to solve a quadratic equation. Ujakar made a mistake in writing down the constant term. He ended up with the roots (4, 3). Keshab made a mistake in writing down the coe cient of x. He got the roots as (3, 2). What will be the exact roots of the original quadratic equation?
A) (6, 1)
B) (-3, -4)
C) (4, 3)
D) (-4, -3)
Answer: Option 'a' is correct.
Explanation: We know that quadratic equation can be written as -(sum of roots)*x+(product of the roots)=0.
Ujakar ended up with the roots (4, 3) so the equation is -(7)*x+(12)=0 where the constant term is wrong.
Keshab got the roots as (3, 2) so the equation is -(5)*x+(6)=0 where the coe cient of x is wrong .
So the correct equation is -(7)*x+(6)=0.
The roots of above equations are (6,1)
|
167 videos|229 docs|95 tests
|
FAQs on Overview: Quadratic Equations - Quantitative Aptitude (Quant) - CAT
| 1. What are the standard forms of a quadratic equation? |  |
| 2. How can we determine the nature of the roots of a quadratic equation? |  |
| 3. What is the relationship between the coefficients and the roots of a quadratic equation? |  |
| 4. What are some common methods to solve quadratic equations? |  |
| 5. How can we find the maximum or minimum value of a quadratic equation? |  |