Packing Fraction | Solid State Physics, Devices & Electronics PDF Download
The packing of atoms in a unit cell of the crystal structure of a material is known as atomic packing.
Atomic packing fraction (APF) is defined as the ratio of the volume of the atoms per unit cell to the volume of the unit cell.
APF = volume of atomic per unit cell/volume of the unit cell
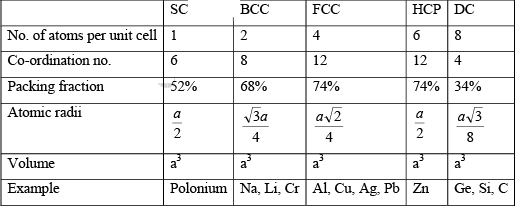
(i) Simple Cubic (SC): In a simple cubic structure, the space lattice is cubic. Atoms are placed at all lattice locations. Therefore, an atom at a lattice location will be in contact with all its six nearest neighbors. Thus the co-ordination number for a simple cubic structure is N=6. In a simple cubic structure, the lattice constant is the cube edge of the conventional unit cell. Thus the lattice constant is the distance between the centers of two neighboring atoms. That is the lattice constant a = 2r, where r is the atomic radius. The atoms at the lattice locations are shared by eight unit cells. Each atom at the lattice location of the unit cell contributes (1/8) to the unit cell. The number of atoms contained in a unit cell in the structure is given by the number of lattice locations in the unit cell multiplied by the contribution of the atom at each location. The effective number of atoms in a unit cell of the simple cubic structure is given by 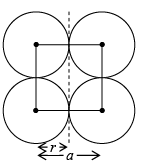
neff = (1/8) x nc + 1/2 x nf + 1 x ni ⇒ neff = (1/8) x 8 + (1/2) x 0 + 1 x 0 = 1
and r = a/2
APF = (neff x volume of each sphere)/volume of each cell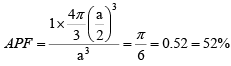
The parameters describing the structure of a simple cubic structure are: 
(ii) Body Centered Cubic (BCC): In body centered cubic structure, the space lattice is cubic. Atoms are placed at all lattice locations and there will be an additional atom at the body center of the cubic unit cell. In this structure, the atoms stacked along the body diagonal of the cubic unit cell are in contact. That is, the atom at the body center of the unit cell will be in contact with all other atoms at the cubic lattice locations of the unit cell. Each atom in the structure will have eight nearest neighbors. Thus, the co-ordination number for a body centered cubic structure is N = 8. In a body centered cubic structure, the lattice constant (a), is the cube edge of the conventional unit cell. The effective number of atoms in a unit cell of the bcc is given by 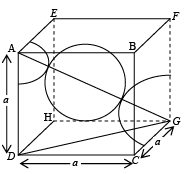 neff = (1/8) x 8 + 1/2 x 0 + 1 x 1 = 2
neff = (1/8) x 8 + 1/2 x 0 + 1 x 1 = 2
neff = 2 and r = (a√3)/4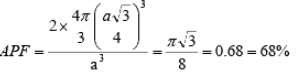
The parameters describing the structure of a body centered cubic structure are :
(iii) Face Centered Cubic (FCC): In a face centered cubic structure, the space lattice is cubic. The conventional unit cell consists of eight small cube lets. Atoms are placed at alternate lattice locations. The atoms stacked along the face diagonal of the cubic unit cell are in contact. The atom at any lattice location of the unit cell will have twelve nearest neighbors. The effective number of atoms in a unit cell of the fcc is given by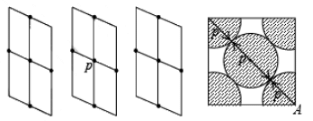
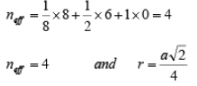

The parameters describing the structure of a face centered cubic structure are :
(iv) Diamond Cubic (DC): Diamond is the crystalline form of carbon. The structure consists of the periodic stacking of carbon atoms in its crystalline state.
A conventional unit cell of structure consists of eight cubic primitive cells. On the basis of the positions of the carbon atoms in the unit cell they are classified as first kind and second kind only for the sake of convenience. Otherwise they are the same carbon atoms. The carbon atoms placed at the FCC positions of the conventional unit cell are the first kind of carbon atoms. Another set of carbon atoms occupy the body centered positions in the primitive cubic cells in the structure. The second type of carbon atoms are placed at the body centers of the alternate cubic primitive cells. These carbon atoms independently form another FCC structure. Therefore, diamond crystal can be regarded as a structure produced by the penetration of one type of carbon atoms forming FCC structure in to the other FCC structure, formed by the second kind of carbon atoms, through a distance equal to three fourth the body diagonal.
If the locations of the atoms in a diamond structure is seen in the primitive part of the unit cell (one of the eight cubelets), they look like a tetrahedra. In these tetrahedra, one atom at the center is bonded to three others in the primitive cell. Periodic stacking of the tetrahedral structure also produces the diamond crystal.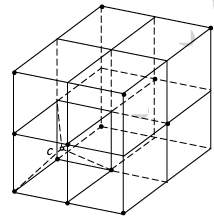
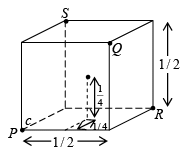
The distance between the two carbon atoms place on the cube edge of the conventional unit cell is the lattice constant and it is, a = 3.567 Au for diamond crystal. This can be treated as the graphical representation of the crystal structure.
The crystal structure can also be illustrated in terms of the co-ordinates of the atoms in the structure. To write the co-ordinates of the carbon atoms in the structure, an orthogonal co-ordinate system is considered. The origin of the co-ordinate system is fixed at one of the carbon atoms. With this co-ordinate system the co-ordinates of the atoms in the structure are shown above.
The effective number of atoms in a unit cell of the diamond cubic is given by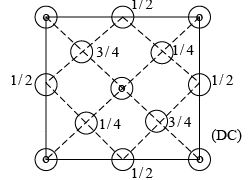
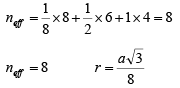
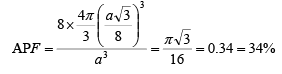

(v) Crystal Structure of Sodium Chloride: Sodium chloride is an ionic crystal. It is a compound of the alkali halide family. Due to the proximity of the sodium atom with a chlorine atom, the valence electron from the sodium atom is transferred to the chlorine atom. With this transfer of an electron, the sodium atom becomes a cation and the chlorine is converted to an anion. Then, these ions are held by the ionic force and the bond that holds the atoms together is ionic.
A conventional unit cell of the structure consists of eight cubic primitive cells. In the conventional unit cell of the crystal, sodium atoms occupy the FCC positions of a cubic structure. Chlorine atoms are placed at the intermediate positions between the sodium atoms. Chlorine atoms independently from an FCC structure similarly sodium atoms also from an independent FCC structure. A unit cell of a sodium chloride crystal can be regarded as the structure formed by the inter-penetration of sodium FCC lattice with the Chlorine FCC lattice through one half of the lattice constant. This can be treated as the graphical representation of the crystal structure.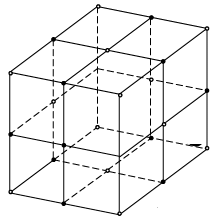
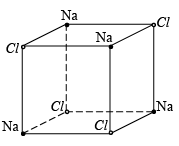
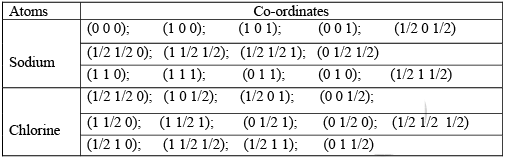
The crystal structure can also be illustrated in terms of the co-ordinates of the atoms in the structure. For this, an orthogonal co-ordinate system is considered. The origins of the co-ordinate system can either be at the location of a chlorine atom or at the location of a sodium atom. With the origin at the location of the sodium atom, the co-ordinates of the sodium and chlorine atoms in the crystal structure are shown below. Sodium chloride is an ionic crystal formed by the transfer of the valence electron from sodium atom to the chlorine atom. Due to this transfer the sodium atom is converted to a cation and the chlorine is converted to an anion. These ions are held by the ionic force and the bond that holds the atoms together is ionic bond. In the unit cell of the compound, chlorine atoms occupy the FCC positions of a cubic structure. Sodium atoms occupy edge center positions.
Example 3: α – Iron is BCC and has a volume density of 7.86 gm/cm3. Calculate α value for the atomic radius of an iron atom. The atomic weight of iron is 55.85 gm/mol.
➤ Information in a Glance
|
91 videos|21 docs|25 tests
|
FAQs on Packing Fraction - Solid State Physics, Devices & Electronics
| 1. What is packing fraction in the context of IIT JAM? |  |
| 2. How is the packing fraction calculated in IIT JAM? |  |
| 3. Why is packing fraction important in IIT JAM? |  |
| 4. How does the packing fraction affect material properties in IIT JAM? |  |
| 5. What are some factors that can affect the packing fraction in IIT JAM? |  |























