Partial Derivatives - Differentiation, Business Mathematics & Statistics | Business Mathematics and Statistics - B Com PDF Download
PARTIAL DERIVATIVES
In differential calculus, so far we have discussed functions of one variable of the form y = f(x). Further one variable may be expressed as a function of several variables. For example, production may be treated as a function of labour and capital and price may be a function of supply and demand. In general, the cost or profit depends upon a number of independent variables, for example, prices of raw materials, wages on labour, market conditions and so on. Thus a dependent variable y depends on a number of independent variables x1 , x2 , x3 ..x n . It is denoted by y = f (x1 , x2 , x3 ..xn ) and is called a function of n variables. In this section, we will restrict the study to functions of two or three variables and their derivatives only.
Definition
Let u = f(x, y) be a function of two independent variables x and y. The derivative of f(x, y) with respect to x, keeping y constant, is called partial derivative of u with respect to x and is denoted by or fx or ux . Similarly we can define partial derivative of f with respect to y. Thus we have
provided the limit exists. (Here y is fixed and Δx is the increment of x)
provided the limit exists. (Here x is fixed and Δy is the increment of y).
The partial derivatives are in general functions of x and y. So we can differentiate functions
partially with respect to x and y. These derivatives are called second order partial derivatives of f(x, y). Second order partial derivatives
Note If f , fx , fy are continuous then fxy= fyx
Homogeneous Function
A function f (x , y) of two independent variable x and y is said to be homogeneous in x and y of degree n if f(tx , ty)=tn f(x , y) for t > 0.
Euler’s Theorem on Homogeneous Function
Theorem : Let f be a homogeneous function in x and y of degree n, then
Corrollary : In general if f(x1 , x2 , x3 ...xm ) is a homogeneous function of degree n in variables x1 , x2 , x3 ...xm , then,
Example 1. It u(x, y) = 1000 - x3 - y 2 + 4x3y6 + 8y, find each of the following.
Solution : u(x, y) = 1000 - x3 - y 2 + 4x3y6 + 8y
Example 2. If f(x, y) = 3x2 + 4y3 + 6xy - x 2y3 + 5 find (i) f (ii) f yy (1, 1) (iii) f xy (2, 1)
Solution :
Example 3.
Solution : We have u = 1/2 log (x 2 + y2 + z2 ) -----------(1)
Differentiating (1) partially with respect to x,
Differentiating (1) partially with respect to y we get,
Differentiating (1) partially with respect to z we get,
Example 4. Verify Euler’s theorem for the function u(x, y) = x3 + y3 + x2y.
Solution : We have u(x, y) = x3 + y3 + x2y. ---------(1)
u(tx , ty)= t3x3 + t 3y3 + t 2x2 (ty)
= t3 (x3 + y3 + x .y) = t3 u(x, y)
∴ u is a homogeneous function of degree 3 in x and y
Differentiating (1) partially with respect to x, we get
Differentiating (1) partially with respect to y, we get
Thus Euler’s Theorem is verified, for the given function.
Example 5.
Solution :
This is a homogeneous function of degree 3 in x and y
Example 6. Without using Euler’s theorem prove that
Solution : We have u = 3x2yz + 4xy2z + 5y4 --------(1)
Differentiating partially with respect to x, we get = 3(2x)yz + 4(1)y2z + 0+ x = 6xyz + 4y 2z
Differentiating (1) partially with respect to y, we get
Differentiating (1) partially with respect to z, we get
Example 7. The revenue derived from selling x calculators and y adding machines is given by R(x, y) = -x2+8x-2y2+6y+2xy+50. If 4 calculators and 3 adding machines are sold, find the marginal revenue of selling (i) one more calculator (ii) one more adding machine.
Solution : (i) The marginal revenue of selling one more calculator is Rx .
∴ At (4, 3), revenue is increasing at the rate of Rs.6 per caculatorsold.
∴Marginal revenue is Rs. 6.
(ii) Marginal Revenue of selling one more adding machine is Ry
Thus at (4, 3) revenue is increasing at the rate of approximately Rs.2 per adding machine. Hence Marginal revenue is Rs.2.
Example 8. Differentiate each of the following functions.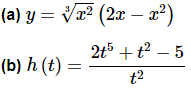
Solution. 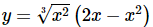
In this function we can’t just differentiate the first term, differentiate the second term and then multiply the two back together. That just won’t work. We will discuss this in detail in the next section so if you’re not sure you believe that hold on for a bit and we’ll be looking at that soon as well as showing you an example of why it won’t work.
It is still possible to do this derivative however. All that we need to do is convert the radical to fractional exponents (as we should anyway) and then multiply this through the parenthesis.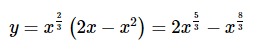
Now we can differentiate the function.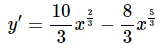
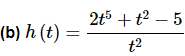
As with the first part we can’t just differentiate the numerator and the denominator and the put it back together as a fraction. Again, if you’re not sure you believe this hold on until the next section and we’ll take a more detailed look at this.
We can simplify this rational expression however as follows.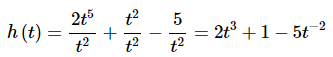
This is a function that we can differentiate.
h′(t) = 6t2 + 10t−3
So, as we saw in this example there are a few products and quotients that we can differentiate. If we can first do some simplification the functions will sometimes simplify into a form that can be differentiated using the properties and formulas in this section.
Before moving on to the next section let’s work a couple of examples to remind us once again of some of the interpretations of the derivative.
Example 9. 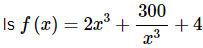 increasing, decreasing or not changing at x = − 2 ?
increasing, decreasing or not changing at x = − 2 ?
Solution. We know that the rate of change of a function is given by the functions derivative so all we need to do is it rewrite the function (to deal with the second term) and then take the derivative.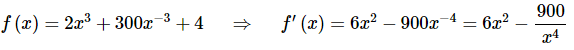
Note that we rewrote the last term in the derivative back as a fraction. This is not something we’ve done to this point and is only being done here to help with the evaluation in the next step. It’s often easier to do the evaluation with positive exponents.
So, upon evaluating the derivative we get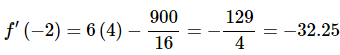
So, at x = − 2 the derivative is negative and so the function is decreasing at x = − 2.
Example 10. Find the equation of the tangent line to 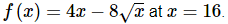
Solution. We know that the equation of a tangent line is given by,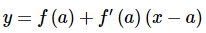
So, we will need the derivative of the function (don’t forget to get rid of the radical).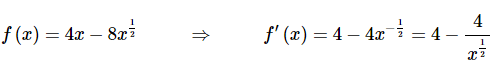
Again, notice that we eliminated the negative exponent in the derivative solely for the sake of the evaluation. All we need to do then is evaluate the function and the derivative at the point in question, x = 16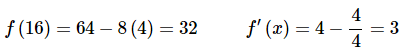
The tangent line is then,
y = 32 + 3(x−16) = 3x − 16
|
124 videos|176 docs
|
FAQs on Partial Derivatives - Differentiation, Business Mathematics & Statistics - Business Mathematics and Statistics - B Com
| 1. What is a partial derivative? |  |
| 2. How are partial derivatives calculated? |  |
| 3. What is the significance of partial derivatives in business mathematics? |  |
| 4. Can partial derivatives be used to optimize business processes? |  |
| 5. Are partial derivatives used in statistical analysis? |  |
















