Partial fraction method of Integration, Business Mathematics & Statistics | Business Mathematics and Statistics - B Com PDF Download
Integration by Partial Fractions
A fraction whose numerator and denominator are both rational and algebraic function can be defined as a rational fraction and such fractions are integrated by splitting the given fraction into partial fractions.
When a function which needs to be integrated is provided in the form of a ratio in which the denominator could be factored, the method to approach would be to break up the single given ratio into a number of a simpler ratio which might be integrated easily. In this method, each factor of the denominator of the given ratio becomes the denominator of a separate fraction so the number resulting out of separate fractions is equal to the of number factors of the given ratio.
The numerators of these separate fractions are then solved from a set of simultaneous equations which impose the condition that the sum of separate fractions is equal to the value of the given.
Integration by partial fractions is one of the integration techniques. That is, integration of a rational function by decomposing the rational function into algebraic sum of compatible rational functions, called partial fractions and then integrate as per sum rule of integration. To use this method, one must be good on partial fractions. That is, you need the knowledge of decomposing a rational expression into simple rational expressions. We will explain this concept and provide necessary formulas in the next section.
Integration of Rational Functions by Partial Fractions
Before studying about the integration of rational fraction by partial fraction, we have to know about the partial fraction.
Definition of Partial Fraction:
If a proper fraction is expressed as the sum of two or more proper fractions, where in the denominators are powers of irreducible polynomials, then each such proper fraction is called a partial fraction of the given fraction.
Any proper rational fraction , where q(x)≠0 can be expressed as a sum of rational fractions, each having a factor of q(x) then, such a fraction is known as a partial fraction.
Rational Fraction:
If p(x) and q(x) are two polynomial equations, then the ratio of these two polynomial equations is given by , where q(x)≠0q(x)≠0, wWhich is called a rational fraction. We have two types of rational fraction
- Proper Rational Fraction
- Improper Rational Fraction
Proper Rational Fraction:
If the degree of the numerator of the rational fraction is less than the degree of the denominator of the rational fraction, then that fraction is called the proper rational fraction.
Improper Rational Fraction:
If the degree of the numerator of the rational fraction is greater than the degree of the denominator of the rational fraction,than that fraction is called as the improper rational fraction. Suppose, the improper fraction is reducible to an integer added to a proper fraction, then the improper rational fraction can be reduced as a sum of polynomial and a proper rational fraction.
Let us take ifis a improper rational fraction,then
= h(x) +
wWhere, h(x) is a polynomial andis a proper rational fraction.
Rules of Partial Fraction

Note that if 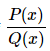 is a proper rational fraction, Step 1 need not be performed. The following table indicates the simpler partial fractions associated to proper rational functions.
is a proper rational fraction, Step 1 need not be performed. The following table indicates the simpler partial fractions associated to proper rational functions.
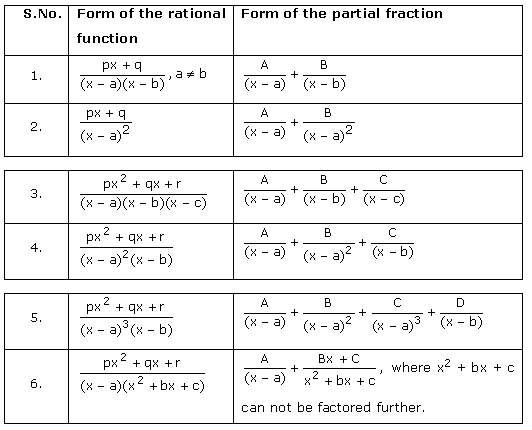
In the above table A, B, C and D are real numbers to be determined suitably.
Method of Partial Fraction
Let us consider the case when the denominator contains non-repeated linear factors,of type
Multiplying both sides by (x - a) (x - b),we get
rx + s = A(x - b) + B(x - a)
Putting x = a, we get
Putting x = b, we get
rb + s = A(b - b) + B(b - a)
rb + s = B(b - a)
ra + s = A(a - b) + B(a - a)
ra + s = A(a - b)
Alternatively,we can equate the coefficients of x and the constant terms we get
r = A + B
s = -bA - aB
Solving these two equations, we will get the values of A and B
Substituting the values of A and B in the given equation, we get the required partial fractions.
Let us consider the case of when the denominator contains repeated linear factors of the type
py2py2 + qy + r = A (y - a) (y - b) + B (y - b) + C (y−a)2(y−a)2
Putting y = a, we get pa2pa2 + qa + r = A(a - a) (a - b) + B( a - b) + C(a−a)2(a−a)2
Putting y = b, we get pb2pb2 + qb + r = C(b−a)2(b−a)2,
These yield the values of B and C.
Now, equating the coefficients of y2 in the above equation, we get
p = A + C,which will yield A.
Examples
Given below are some of the examples on Integration by Partial Fractions:
Substituting the values of A, B and C in the above equation, we shall obtain the required partial fractions.
Solved Examples
The given proper rational fraction is resolved in to the sum of two simpler rational fractions.
Now, using (x - 2)(x - 3)22(x22 + 2x + 4) as the common denominator and simplifying, the numerator on the right side becomes as,
Equating the numerators of both sides,
This is an identity. The coefficients of each power of the variable must be equal and that way, solutions for A, B, C, D and E can be made. But, that process is tedious. Instead, it will be easier to assume some compatible values which can eliminate some terms.
Assuming x = 0 and plugging in the values of A and C, - 4 = 36 + 24B - 16 +18E, or, 4B + 3E = -4 (1)
Assuming x = 1 and plugging in the values of A and C,
3 - 23 + 64 - 52 - 4 = 28 + 14B - 14 - 4D - 4E, or, 14B - 4D - 4E = -26 (2)
Assuming x = -1 and plugging in the values of A and C,
3 + 23 + 64 + 52 - 4 = 48 + 36B - 18 + 48D - 48E, or, 3B + 4D - 4E = 9 (3)
Adding equations (2) and (3) vertically, 17B - 8E = -17 (4)
From (1), we get B = (- 4 - 3 E)/(4) and plugging this in equation (4),
(17)(- 4 - 3E)/(4) + 3E = -17 or, E = 0
Since E = 0, from equation (4) we get B = -1.
Plugging in E = 0 and B = -1, in equation (1) or (2), we get D = 3.
Therefore,
And hence,
Question 2: Integrate the following rational fraction
Solution:
Divide the numerator by the denominator, since the rational fraction is improper.
⇒ 2x + 1 = A(x+1) + B(x - 1)
Put x = 1, A = 3/2
Put x = -1, B = 1/2
Substituting the values of A and B in (2) we have
∴ From (1), we have
Question 3: Integrate the following partial fraction
Solution:
2x + 1 = A(x - 2) + B(x - 1)
Put x = 1 in the above equation,we get 2 + 1 = A(1 - 2) + B(0)
3 = - A
A = -3
Again, put x = 2
2(2) + 1 = A.(0) + B(2-1)
B =5
Question 4: is the rational fraction.
Solution:
This can be decomposed as,
Practice Problems
Here, are given few practice problems. You may solve them in order to master the concept of integration by partial fractions.
Evaluate the integrals of following using techniques of partial fractions.
|
124 videos|176 docs
|
FAQs on Partial fraction method of Integration, Business Mathematics & Statistics - Business Mathematics and Statistics - B Com
| 1. What is the partial fraction method of integration? |  |
| 2. When is the partial fraction method used in integration? |  |
| 3. How do you decompose a rational function using the partial fraction method? |  |
| 4. Can the partial fraction method be used for all rational functions? |  |
| 5. Are there any limitations or challenges when using the partial fraction method? |  |





















