Percentages Questions with Answers | Quantitative for GMAT PDF Download
Q.1. If the price of petrol increases by 25% and Raj intends to spend only an additional 15% on petrol, by how much % will he reduce the quantity of petrol purchased?
(a) 10%
(b) 12%
(c) 8%
(d) 6.67%
(e) 12.5%
Ans. (c)
Solution.
Let the price of 1 litre of petrol be Rs. x and let Raj initially buy 'y' litres of petrol.
Therefore, he would have spent Rs. xy on petrol.
When the price of petrol increases by 25%, the new price per litre of petrol is 1.25x.
Raj intends to increase the amount he spends on petrol by 15%.
i.e., he is willing to spend xy + 15% of xy = 1.15xy
Let the new quantity of petrol that he can get be 'q'.
Then,
1.25x * q = 1.15xy
Or
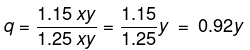
As the new quantity that he can buy is 0.92y, he gets 0.08y lesser than what he used to get earlier. Or a reduction of 8%.
Q.2. A shepherd has 1 million sheeps at the beginning of Year 2000. The numbers grow by x% (x > 0) during the year. A famine hits his village in the next year and many of his sheeps die. The sheep population decreases by y% during 2001 and at the beginning of 2002 the shepherd finds that he is left with 1 million sheeps. Which of the following is correct?
(a) x > y
(b) y > x
(c) x = y
(d) Cannot be determined
Ans. (a)
Solution.
Let us assume the value of x to be 10%.
Therefore, the number of sheep in the herd at the beginning of year 2001 (end of 2000) will be 1 million + 10% of 1 million = 1.1 million
In 2001, the numbers decrease by y% and at the end of the year the number sheep in the herd = 1 million.
i.e., 0.1 million sheep have died in 2001.
In terms of the percentage of the number of sheep alive at the beginning of 2001, it will be (0.1/1.1)*100 % = 9.09%.
From the above illustration it is clear that x > y.
Q.3. In an election contested by two parties, Party D secured 12% of the total votes more than Party R. If party R got 132,000 votes and there are no invalid votes, by how many votes did it lose the election?
(a) 300,000
(b) 168,000
(c) 36,000
(d) 24,000
Ans. (c)
Solution.
Let the percentage of the total votes secured by Party D be x%
Then the percentage of total votes secured by Party R = (x - 12)%
As there are only two parties contesting in the election, the sum total of the votes secured by the two parties should total up to 100% i.e., x + x - 12 = 100
2x - 12 = 100
or 2x = 112 or x = 56%.
If Party D got 56% of the votes, then Party got (56 - 12) = 44% of the total votes.
44% of the total votes = 132,000
i.e.,44/100*T = 132,000
T = 132000*100/44 = 300,000 votes.
The margin by which Party R lost the election = 12% of the total votes
= 12% of 300,000 = 36,000.
Q.4. A candidate who gets 20% marks fails by 10 marks but another candidate who gets 42% marks gets 12% more than the passing marks. Find the maximum marks.
(a) 50
(b) 100
(c) 150
(d) 200
Ans. (b)
Solution.
From the given statement pass percentage is 42% - 12% = 30%
By hypothesis, 30% of x - 20% of x = 10 (marks)
i.e., 10% of x = 10
Therefore, x = 100 marks.
Q.5. When processing flower - nectar into honeybees' extract, a considerable amount of water gets reduced. How much flower - nectar must be processed to yield 1 kg of honey, if nectar contains 50% water, and the honey obtained from this nectar contains 15% water?
(a) 1.5 kgs
(b) 1.7 kgs
(c) 3.33 kgs
(d) None of these
Ans. (b)
Solution.
Flower-nectar contains 50% of non-water part.
In honey this non-water part constitutes 85% (100-15).
∴ 0.5 X Amount of flower-nectar = 0.85 X Amount of honey = 0.85 X 1 kg
Therefore, amount of flower-nectar needed = (0.85/0.5) * 1 kg = 1.7 kg.
Q.6. A vendor sells 60 percent of apples he had and throws away 15 percent of the remainder. Next day he sells 50 percent of the remainder and throws away the rest. What percent of his apples does the vendor throw?
(a) 17
(b) 23
(c) 77
(d) None of these
Ans. (b)
Solution.
Let the number of apples be 100.
On the first day he sells 60% apples ie.,60 apples. Remaining apples =40.
He throws 15% of the remaining i.e., 15% of 40 = 6.Now he has 40 - 6 = 34 apples
The next day he throws 50% of the remaining 34 apples i.e., 17.
Therefore, in all he throws 6 + 17 =23 apples.
Q.7. If the cost price of 20 articles is equal to the selling price of 16 articles, what is the percentage profit or loss made by the merchant?
(a) 20% Profit
(b) 25% Loss
(c) 25% Profit
(d) 33.33% Loss
Ans. (c)
Solution.
Let Cost price of 1 article be Re.1.
Therefore, Cost price of 20 articles = Rs.20.
Selling price of 16 articles = Rs.20
Therefore, Selling price of 20 articles = (20/16)*20 = 25
Profit = Selling price - Cost price
= 25 - 20 = 5
Percentage of profit = (profit/cost price)*100.
= (5/20)*100 = 25% Profit
Q.8. 30% of the men are more than 25 years old and 80% of the men are less than or equal to 50 years old. 20% of all men play football. If 20% of the men above the age of 50 play football, what percentage of the football players are less than or equal to 50 years?
(a) 15%
(b) 20%
(c) 80%
(d) 70%
Ans. (c)
Solution.
20% of the men are above the age of 50 years. 20% of these men play football. Therefore, 20% of 20% of 4% of the total men are football players above the age of 50 years.
20% of the men are football players. Therefore, 16% of the men are football players below the age of 50 years.
Therefore, the % of men who are football players and below the age of 50 = (16/20) * 100 = 80%
Q.9. If the price of petrol increases by 25%, by how much must a user cut down on his petrol consumption so that his expenditure on petrol remains unchanged?
(a) 25%
(b) 16.67%
(c) 20%
(d) 33.33%
Ans. (c)
Solution.
Let the price of petrol be Rs.100 per litre. Let the user use 1 litre of petrol.
Therefore, his expense on petrol = 100 * 1 = Rs.100
Now, the price of petrol increases by 25%. Therefore, the new price of petrol = Rs.125.
As he has to maintain his expenditure on petrol constant, he will be spending only Rs.100 on petrol.
Let 'x' be the number of litres of petrol he will use at the new price.
Therefore, 125 * x = 100 => x = 100/125 = 4/5 =0.8 litres.
He has cut down his petrol consumption by 0.2 litres = 0.2/1 * 100 = 20% reduction.
There is a short cut for solving this problem.
If the price of petrol has increased by 25%, it has gone up 1/4th of its earlier price.
Therefore, the % of reduction in petrol that will maintain the amount of money spent on petrol constant = 1/4+1 = (1/5) 20%
i.e. Express the percentage as a fraction. Then add the numerator of the fraction to the denominator to obtain a new fraction. Convert it to percentage - that is the answer.
Q.10. Peter got 30% of the maximum marks in an examination and failed by 10 marks. However, Paul who took the same examination got 40% of the total marks and got 15 marks more than the passing marks. What was the passing marks in the examination?
(a) 35
(b) 250
(c) 75
(d) 85
Ans. (d)
Solution.
Let 'x' be the maximum marks in the examination.
Therefore,
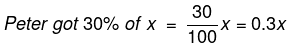
and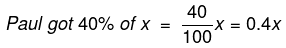
In terms of the maximum marks Paul got 0.4x - 0.3x = 0.1x more than Peter. -- (1)
The problem however, states that Paul got 15 marks more than the passing mark and Peter got 10 marks less than the passing mark.
Therefore, Paul has got 15 + 10 = 25 marks more than Peter. -- (2)
Equating (1) and (2), we get
0.1x = 25
=> x = 25/0.1 = 250
'x' is the maximum mark and is equal to 250 marks.
We know that Peter got 30% of the maximum marks.
Therefore, Peter got (30/100)*250 = 75 marks.
We also know that Peter got 10 marks less than the passing mark.
Therefore, the passing mark will be 10 marks more than what Peter got = 75 + 10 = 85.
Q.11. A report consists of 20 sheets each of 55 lines and each such line consists of 65 characters. This report is reduced onto sheets each of 65 lines such that each line consists of 70 characters. The percentage reduction in number of sheets is closest to:
(a) 20%
(b) 5%
(c) 30%
(d) 35%
Ans. (a)
Solution.
No. of Characters in one line = 65
No. of characters in one sheet = No. of lines × No. of characters per line = 55 × 65
Total number of characters = No. of sheets × No. of characters in one sheet = 20 × 55 × 65 = 71500
If the report is retyped: New sheets have 65 lines, with 70 characters per line
No. of characters in one sheet = 65 × 70
Number of pages required,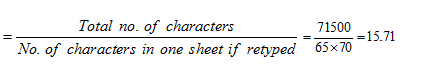
Hence, 16 pages will be required if report is retyped.
Hence, reduction of (20 – 16) = 4 pages
% reduction is = (4/20) x 100 = 20%
Q.12. The number of votes not cast for the PNC Party increased by 25% in the National General Election over those not cast for it in the previous Assembly Polls, and the PNC Party lost by a majority twice as large as that by which it had won the Assembly Polls. If a total 2,60,000 people voted each time, how many voted for the PNC Party in the previous Assembly Polls?
(a) 1,10,000
(b) 1,50,000
(c) 1,40,000
(d) 1,20,000
Ans. (c)
Solution.
Total Votes = 2,60,000
Let x voters voted against the party in the Assembly Poll.
Then votes in favour = 260000 – x
Therefore, majority of votes by which party won in previous poll = 260000– x – x = 260000 – 2x
Next year votes against the PNC party increase by 25%
So, votes against the party in general election = 1.25 x
And votes polled in favour of the party = total votes – votes against = 260000 – 1.25x
Therefore, majority of votes by which party lost in general election
= 1.25x – (260000 – 1.25x) = 2.5x – 260000
It is given that, PNC Party lost by a majority twice as large as that by which it had won the Assembly Polls.
Therefore, 2.5x – 260000 = 2(260000 – 2 x)
⇒ 2.5x – 260000 = 2 260000 – 4x
⇒ 6.5x = 3260000 ⇒ x = 1,20,000
Therefore, votes polled by the voters for the party in Assembly Polls for previous year
= (2,60,000 – x) = (2,60,000 – 1,20,000) = 1,40,000.
Q.13. 2/5th of the voters promise to vote for A and the rest promised to vote for B. Of these, on the last day 15% of the voters went back of their promise to vote for A and 25% of voters went back of their promise to vote for B, and A lost by 200 votes. Then, the total number of voters is:
(a) 10000
(b) 11000
(c) 9000
(d) 9500
Ans. (a)
Solution.
Let x be the total number of voters
Voters promised to A = 2/5 x
Voters backed out = 15% of 2/5 x
Voters promised to B = 3/5 x
Voters backed out = 25% of 3/5 x
Total Number of votes for A = 2/5 x – 15% of 2/5 x + 25% of 3/5 x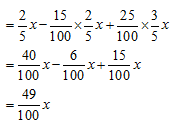
Total Number of votes for B = 3/5 x - 25% of 3/5 x + 15% of 2/5 x

Given difference in votes is 200
Therefore,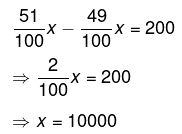
So, there were 10000 voters.
Q.14. A person who has a certain amount with him goes to market. He can buy 50 oranges or 40 mangoes. He retains 10% of the amount for taxi fares and buys 20 mangoes and of the balance, he purchases oranges. Number of oranges he can purchase is:
(a) 36
(b) 40
(c) 15
(d) 20
Ans. (d)
Solution.
The person can buy 50 oranges or 40 mangoes.
Let the price of one orange be Rs. x
Total amount the person has = Rs. 50x
40 mangoes cost 50x, So one mango costs 1.25x
10% of the total amount is retained for taxi fare = 10% of 50x = 5x
20 mangoes bought for 20 * 1.25 x = 25x
Money left with the person = 50 x – (Taxi fare) – (Mangoes cost)
= 50 x – 5 x – 25 x = 20 x
One Orange was for Rs. x, Therefore, 20 oranges can be bought with Rs. 20 x
Thus, the person bought 20 oranges.
Q.15. Forty per cent of the employees of a certain company are men and 75% of the men earn more than Rs. 25,000 per year. If 45% of the company’s employees earn more than Rs. 25,000 per year, what fraction of the women employed by the company earn Rs. 25,000 or less per year?
(a) 2/11
(b) 1/4
(c) 1/3
(d) 3/4
Ans. (d)
Solution.
Let the total number of employees in the company be x
Then the number of men and women be 0.4x and 0.6x respectively.
75% of men earn more than Rs. 25000 => 0.75 x 0.4 x = 0.3 x
Total number of employees earning more than Rs. 25000 = 45% x = 0.45 x
Number of women earning more than Rs. 25000 = Total employees earning more than Rs. 25000 – total number of Men earning more than Rs. 25000
= 0.45 x – 0.30 x = 0.15 x
Number of the women earning Rs. 25000 or less = 0.60 x – 0.15 x = 0.45 x
Fraction of the women employed by the company who earn Rs. 25000 or less
(0.45 x/0.60 x) = 45/60 = ¾
Alternate Solution:
Let there are 40 men and 60 women in the company. Now out of 40 men, 75% i.e. 30 earn more than Rs 25000 and 45% of the total employees i.e. 45 employees earn more than Rs 25000.
Hence, there are 45 – 30 = 15 women who earn more than Rs. 25000. So, 60 – 15 = 45 women earn less than Rs. 25000.
Hence, the required fraction = 45/60 = ¾
|
115 videos|106 docs|113 tests
|
FAQs on Percentages Questions with Answers - Quantitative for GMAT
| 1. What is the concept of percentages? |  |
| 2. How do you calculate percentages? |  |
| 3. What are some common applications of percentages in everyday life? |  |
| 4. How can I find the percentage increase or decrease between two values? |  |
| 5. How can I calculate the percentage of a number? |  |

|
Explore Courses for GMAT exam
|

|


















