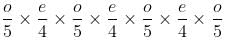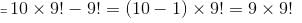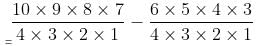This EduRev document offers 20 Multiple Choice Questions (MCQs) from the topic Permutation & Combination (Level - 1). These questions are of Level - 1 difficulty and will assist you in the preparation of CAT & other MBA exams. You can practice/attempt these CAT Multiple Choice Questions (MCQs) and check the explanations for a better understanding of the topic.
Question for Practice Questions Level 1: Permutation & Combination - 2
Try yourself:The number of squares in a board having 10 rows and 9 columns is
Explanation
Number of squares in a board having m rows and n columns (m ≥ n) = m × n + (m - 1) × (n - 1) + (m - 2) × (n - 2) ... (m - n + 1) × 1
Here, m = 10 and n = 9
Number of squares = 10 × 9 + 9 × 8 + 8 × 7 + 7 × 6 + 6 × 5 + 5 × 4 + 4 × 3 + 3 × 2 + 2 × 1
= 90 + 72 + 56 + 42 + 30 + 20 + 12 + 6 + 2 = 330
Report a problem
Question for Practice Questions Level 1: Permutation & Combination - 2
Try yourself:Find the last digit of the sum 1! + 2! + 3! + ………… + 100!.
Explanation
1! = 1
2! = 2
3! = 6
4! = 24
5! = 120
6! = 6 x 5! = shall always have 0 in the unit's place.
And the same is the case for 7!, 8! and the succeeding factorials.
Hence, unit's digit shall be the unit's digit in 1 + 2 + 6 + 24 + 0 = 3.
Report a problem
Question for Practice Questions Level 1: Permutation & Combination - 2
Try yourself:Two packs of 52 cards are shuffled together. The number of ways in which a man can be dealt 26 cards, so that he does not get two cards of the same suit and same denominations is
Explanation
26 cards can be chosen out of 52 cards in 52C26 ways. There are two ways in which each card can be dealt, either from the first pack or from the second.
Total number of ways = 52C26 . 226
Report a problem
Question for Practice Questions Level 1: Permutation & Combination - 2
Try yourself:In how many ways will a particular person be found among those six if six persons are to be selected out of ten?
Explanation
We require that the particular person is found in every group of 6 people out of a total of 10. As this person is common to all groups of 6, we will have to consider the number of ways of choosing the remaining 5 persons out of the other 9. This can be done in 9C5 ways = 126 ways.
Report a problem
Question for Practice Questions Level 1: Permutation & Combination - 2
Try yourself:A 7-character code is such that only even digits occur at even places and only odd digits occur at odd places, e.g. 1436789. How many such codes can be made from digits 1-9, if repetition of digits is allowed?
Explanation
Odd digits: 1, 3, 5, 7, and 9
Even digits: 2, 4, 6, and 8
Number of ways to fill an odd place = 5
Number of ways to fill an even place = 4
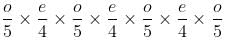
Therefore,
Total number of cases = (5)4 × (4)3
Report a problem
Question for Practice Questions Level 1: Permutation & Combination - 2
Try yourself:Five boxes are numbered from 1 to 5. A ball is to be placed in each box and balls of three different colours Red, Blue and Green are available. After this, a code is generated as *****, where the first * represents the first letter of colour of the ball in that box, and so on so forth (e.g. RBBGR and RBBRG are two different codes). How many different codes will result?
Explanation
For every box, we have three different possibilities of colours.
Therefore, total number of possibilities = 3 × 3 × 3 × 3 × 3
Report a problem
Question for Practice Questions Level 1: Permutation & Combination - 2
Try yourself:If 10P5 × 4P3 = 6P5 × X × 2, then X is
Explanation
10P5 × 4P3 = 6P5 × X × 2
10 × 9 × 8 × 7 × 6 × 4 × 3 × 2 = 6 × 5 × 4 × 3 × 2 × X × 2
9 × 8 × 7 = X then X = 9P3
Report a problem
Question for Practice Questions Level 1: Permutation & Combination - 2
Try yourself:What is the difference between total number of arrangements when 10 members are arranged in a row and in a circle?
Explanation
Total number of arrangements when n members are arranged in a row = n!
Total number of arrangements when n members are arranged in a circle = (n - 1)!
Difference = n! - (n - 1)!
Difference = 10! - 9!
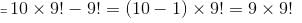
Report a problem
Question for Practice Questions Level 1: Permutation & Combination - 2
Try yourself:How many numbers lying between 600 and 700 can be formed with the digits 0-9, where 7 occurs at exactly one of the positions (repetition is allowed)?
Explanation
Let 7 occur in the units place. So, the units digit can be placed in 1 way. The tens digit can be placed by the rest of 9 numbers. The hundreds digit can be placed by 6 only, i.e. one way.
As the numbers are between 600 and 700, number of ways = 1 × 9 × 1 = 9
Now, let 7 occur in the tens place. The units place can be filled by any of the numbers from 0-9 except 7.
The hundreds place can be filled in one way (by only 6). So, total 9 ways. 7 can't occur in the hundreds place.
∴ Total number of ways in which numbers can be formed = 9 + 9 = 18
Report a problem
Question for Practice Questions Level 1: Permutation & Combination - 2
Try yourself:In how many ways can 6 awards be distributed among 9 actors, if each actor can get any number of awards?
Explanation
For 1st award: We have 9 options to distribute.
And for 2nd award: Again we have 9 options to distribute (Any actor can get any number of award)
Similarly for each others we have 9 options.
Total number of ways when repetition is allowed = 9 × 9 × 9 × 9 × 9 × 9 = 96
So, total number of ways of distributing the awards = 96
Report a problem
Question for Practice Questions Level 1: Permutation & Combination - 2
Try yourself:There are 6 black balls and 4 white balls in a box. In how many ways can 4 balls be selected, in which there is at least one white ball?
Explanation
Selecting 4 balls out of 10 balls having at least 1 white ball = Selecting 4 balls out of 10 balls - Selecting 4 balls out of 10 balls having no white ball
= 10C4 - 6C4
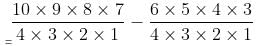
= 210 - 15 = 195
Report a problem
Question for Practice Questions Level 1: Permutation & Combination - 2
Try yourself:An apparel shop has 15 different shades of T-shirts and 35 different shades of shorts. In how many different ways can one buy two items containing only one shade of T-shirt and one shade of shorts?
Explanation
For every single shade of a T-shirt, one can make 35 distinct pairs with differently shaded shorts. Since there are 15 shades of T-shirts, number of ways = 15 × 35 = 525
Report a problem
Question for Practice Questions Level 1: Permutation & Combination - 2
Try yourself:How many numbers of 3 digits can be formed with the digits 1, 2, 3, 4, 5 (repetition of digits not allowed)?
Explanation
The correct option is C 60
Three digits can be formed in
5P3 ways that is
5!/(5-3)! = 60
Report a problem
Question for Practice Questions Level 1: Permutation & Combination - 2
Try yourself:In how many ways can a person send invitation cards to 6 of his friends if he has four servants to distribute the cards?
Explanation
Each invitation card can be sent in 4 ways. Thus, 4 × 4 × 4 × 4 × 4 × 4 = 46.
Report a problem
Question for Practice Questions Level 1: Permutation & Combination - 2
Try yourself:In how many ways can 7 Indians, 5 Pakistanis and 6 Dutch be seated in a row so that all persons of the same nationality sit together?
Explanation
We need to assume that the 7 Indians are 1 person, so also for the 6 Dutch and the 5 Pakistanis. These 3 groups of people can be arranged amongst themselves in 3! ways. Also, within themselves the 7 Indians the 6 Dutch and the 5 Pakistanis can be arranged in 7!, 6! And 5! ways respectively. Thus, the answer is 3! × 7! × 6! × 5!.
Report a problem
Question for Practice Questions Level 1: Permutation & Combination - 2
Try yourself:There are 4 qualifying examinations to enter into Oxford University: RAT, BAT, SAT, and PAT. An Engineer cannot go to Oxford University through BAT or SAT. A CA on the other hand can go to the Oxford University through the RAT, BAT & PAT but not through SAT. Further there are 3 ways to become a CA(viz., Foundation, Inter & Final). Find the ratio of number of ways in which an Engineer can make it to Oxford University to the number of ways a CA can make it to Oxford University.
Explanation
An engineer can make it through in 2 ways, while a CA can make it through in 3 ways. Required ratio is 2:3. Option (b) is correct.
Report a problem
Question for Practice Questions Level 1: Permutation & Combination - 2
Try yourself:If nC3 = nC8, find n.
Explanation
Use the property nCr = nCn-r to see that the two values would be equal at n = 11 since 11C3 = 11C8.
Report a problem
Question for Practice Questions Level 1: Permutation & Combination - 2
Try yourself:In how many ways can the letters of the word PATNA be rearranged?
Explanation
Rearrangements do not count the original arrangements. Thus, 5!/2! – 1 = 59 ways of rearranging the letters of PATNA.
Report a problem
Question for Practice Questions Level 1: Permutation & Combination - 2
Try yourself:If 10Pr = 720, find r.
Explanation
10P3 would satisfy the value given as 10P3 = 10 × 9 × 8 = 720.
Report a problem
Question for Practice Questions Level 1: Permutation & Combination - 2
Try yourself:How many numbers of four digits can be formed with the digits 0, 1, 2, 3 (repetition of digits being allowed?
Explanation
Report a problem