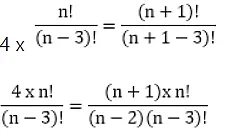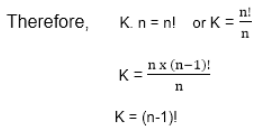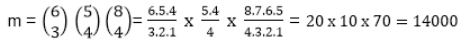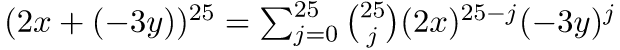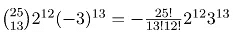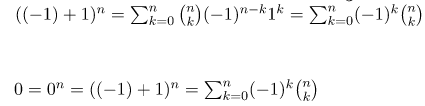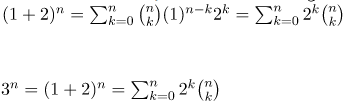Permutations, Combinations & Binomial Coefficients | Engineering Mathematics - Engineering Mathematics PDF Download
Permutation
Any arrangement of a set of n objects in a given order is called Permutation of Object. Any arrangement of any r ≤ n of these objects in a given order is called an r-permutation or a permutation of n object taken r at a time.
It is denoted by P (n, r)
P (n, r) = 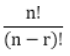
Theorem: Prove that the number of permutations of n things taken all at a time is n!.
Proof: We know that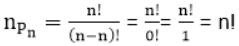
Example: 4 x np3 = n + 1P3
4 (n-2) = (n+1)
4n - 8 = n+1
3n = 9
n = 3.
Permutation with Restrictions:
- The number of permutations of n different objects taken r at a time in which p particular objects do not occur is
n - npr - The number of permutations of n different objects taken r at a time in which p particular objects are present is
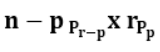
Example: How many 6-digit numbers can be formed by using the digits 0, 1, 2, 3, 4, 5, 6, 7, 8 if every number is to start with '30' with no digit repeated?
All the numbers begin with '30.'So, we have to choose 4-digits from the remaining 7-digits.
∴ Total number of numbers that begins with '30' is
Permutations with Repeated Objects
Theorem: Prove that the number of different permutations of n distinct objects taken at a time when every object is allowed to repeat any number of times is given by nr.
Proof: Assume that with n objects we have to fill r place when repetition of the object is allowed.
Therefore, the number of ways of filling the first place is = n
The number of ways of filling the second place = n
.............................
.............................
The number of ways of filling the rth place = n
Thus, the total number of ways of filling r places with n elements is
= n. n. n..............r times = nr.
Circular Permutations
- A permutation which is done around a circle is called Circular Permutation.
Example: In how many ways can get these letters a, b, c, d, e, f, g, h, i, j arranged in a circle?
(10 - 1) = 9! = 362880
Theorem: Prove that the number of circular permutations of n different objects is (n-1)!
Proof: Let us consider that K be the number of permutations required.
For each such circular permutations of K, there are n corresponding linear permutations. As shown earlier, we start from every object of n object in the circular permutations. Thus, for K circular permutations, we have K...n linear permutations.
Hence Proved.
Combination
- A Combination is a selection of some or all, objects from a set of given objects, where the order of the objects does not matter. The number of combinations of n objects, taken r at a time represented by nCr or C (n, r).
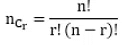
Proof: The number of permutations of n different things, taken r at a time is given by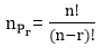
As there is no matter about the order of arrangement of the objects, therefore, to every combination of r things, there are r! arrangements i.e.,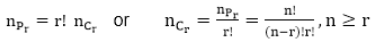
Thus,
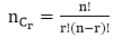
Example: A farmer purchased 3 cows, 2 pigs, and 4 hens from a man who has 6 cows, 5 pigs, and 8 hens. Find the number m of choices that the farmer has.
The farmer can choose the cows in C (6, 3) ways, the pigs in C (5, 2) ways, and the hens in C (8, 4) ways. Thus the number m of choices follows:
Binomial Coefficients
The r -combinations from a set of n elements if denoted by 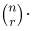 This number is also called a binomial coefficient since it occurs as a coefficient in the expansion of powers of binomial expressions.
This number is also called a binomial coefficient since it occurs as a coefficient in the expansion of powers of binomial expressions.
The binomial theorem gives a power of a binomial expression as a sum of terms involving binomial coefficients.
Formally,
Let x and y be variables and n be a non-negative integer. Then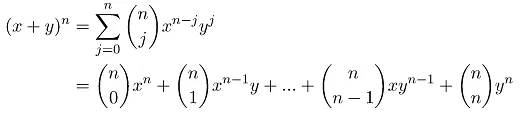
Example 1: What is the coefficient of x12y13 in the expansion of (2x - 3y)25?
(2x - 3y)25 = (2x + (-3y))25 .
By the binomial theorem-
Since the power of y is 13, j = 13 .
Therefore the coefficient of x12y13 is-
Example 2: Prove that 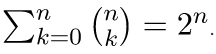
If we put x = 1 and y = 1 in the binomial theorem expression, we get-
Example 3: Prove that 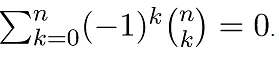
If we put x = -1 and y = 1 in the binomial theorem expression, we get-
Example 4: Prove that 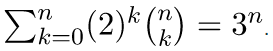
If we put x = 1 and y = 2 in the binomial theorem expression, we get-
|
65 videos|129 docs|94 tests
|