Phase Space, Micro-canonical, and Canonical - CSIR-NET Physical Sciences | Physics for IIT JAM, UGC - NET, CSIR NET PDF Download
Basic principles.
Here we introduce microscopic statistical description in the phase space and describe two principal ways (microcanonical and canonical) to derive thermodynamics from statistical mechanics.
1.1 Distribution in the phase space
We consider macroscopic bodies, systems and subsystems. We define probability for a subsystem to be in some ΔpΔq region of the phase space as the fraction of time it spends there. . We introduce the statistical distribution in the phase space as density. dw = ρ(p, q)dpdq. By definition, the average with the statistical distribution is equivalent to the time average.
The main idea is that ρ(p, q) for a subsystem does not depend on the initial states of this and other subsystems so it can be found without actually solving equations of motion. We define statistical equilibrium as a state where macroscopic quantities equal to the mean values. Statistical independence of macroscopic subsystems at the absence of long-range forces means that the distribution for a composite system ρ12 is factorized. ρ12 = ρ1ρ2.
Now, we take the ensemble of identical systems starting from different points in phase space. If the motion is considered for not very large time it is conservative and can be described by the Hamiltonian dynamics (that is and
then the °ow in the phase space is incompressible. That gives the Liouville theorem.
that is the statistical distribution is conserved along the phase tra jectories of any subsystem. As a result, equilibrium ρ must be expressed solely via the integrals of motion. Since ln ρ is an additive quantity then it must be expressed linearly via the additive integrals of motions which for a general mechanical system are energy E (p, q), momentum P(p, q) and the momentum of momentum M(p, q).
Here αa is the normalization constant for a given subsystem while the seven constants β , c, d are the same for all subsystems (to ensure additivity) and are determined by the values of the seven integrals of motion for the whole system. We thus conclude that the additive integrals of motion is all we need to get the statistical distribution of a closed system (and any subsystem), those integrals replace all the enormous microscopic information.
Considering system which neither moves nor rotates we are down to the single integral, energy. For any subsystem (or any system in the contact with thermostat) we get Gibbs' canonical distribution
For a closed system with the energy E0, Boltzmann assumed that all microstates with the same energy have equal probability (ergodic hypothesis) which gives the microcanonical distribution.
Usually one considers the energy fixed with the accuracy Δ so that the microcanonical distribution is
where is the volume of the phase space occupied by the system
For example, for N noninteracting particles (ideal gas) the states with the energy are in the p-space near the hyper-sphere with the radius
. Remind that the surface area of the hyper-sphere with the radius R in 3N -dimensional space is
and we have
1.2 Microcanonical distribution
One can link statistical physics with thermodynamics using either canonical or microcanonical distribution. We start from the latter and introduce the entropy as
This is one of the most important formulas in physics (on a par with F = ma ,
Noninteracting subsystems are statistically independent so that the statistical weight of the composite system is a product and entropy is a sum.
For interacting subsystems, this is true only for short-range forces in the thermodynamic limit N → ∞. Consider two subsystems, 1 and 2, that can exchange energy. Assume that the indeterminacy in the energy of any subsystem, Δ, is much less than the total energy E . Then
We denote the values that correspond to the maximal term in the sum (9), the extremum condition is evidently
It is obvious that If the system consists of N particles and
where the last term is negligible.
Identification with the thermodynamic entropy can be done considering any system, for instance, an ideal gas (7). S (E , V , N ) = (3N/) ln E + f (N, V ). Defining temperature in a usual way, we get the correct expression E = 3N T/2. We express here temperature in the energy units. To pass to Kelvin degrees, one transforms T → kT and S → kS where the Boltzmann constant k = 1.38 Δ 1023 J/K .
The value of classical entropy (8) depends on the units. Proper quantitative definition comes from quantum physics with being the number of microstates that correspond to a given value of macroscopic parameters.
In the quasi-classical limit the number of states is obtained by dividing the phase space into units with Note in passing that quantum particles (atoms and molecules) are indistinguishable so one needs to divide
(7) by the number of transmutations N ! which makes the resulting entropy of the ideal gas extensive. S (E , V , N ) = (3N/2) ln E /N + N ln V /N +const1.
The same definition (entropy as a logarithm of the number of states) is true for any system with a discrete set of states. For example, consider the set of N two-level systems with levels 0 and ε. If energy of the set is E then there are L = E = ε upper levels occupied. The statistical weight is determined by the number of ways one can choose L out of N .
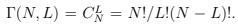 We can now define entropy (i.e. find the fundamental relation): S(E, N) = ln
We can now define entropy (i.e. find the fundamental relation): S(E, N) = ln . Considering
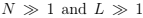 we can use the Stirling formula in the form
we can use the Stirling formula in the form 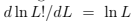 and derive the equation of state (temperature-energy relation)
and derive the equation of state (temperature-energy relation) 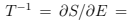
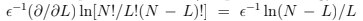 and specific heat C = dE/dT = N(
and specific heat C = dE/dT = N(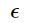 /T)2 2cosh-1 (
/T)2 2cosh-1 (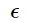 /T). Note that the ratio of the number of particles on the upper level to those on the lower level is exp(- ε /T ) (Boltzmann relation). Specific heat turns into zero both at low temperatures (too small portions of energy are "in circulation") and in high temperatures (occupation numbers of two levels already close to equal).
/T). Note that the ratio of the number of particles on the upper level to those on the lower level is exp(- ε /T ) (Boltzmann relation). Specific heat turns into zero both at low temperatures (too small portions of energy are "in circulation") and in high temperatures (occupation numbers of two levels already close to equal).
The derivation of thermodynamic fundamental relation S (E ,......) in the microcanonical ensemble is thus via the number of states or phase volume.
1.3 Canonical distribution
We now consider small subsystem or system in a contact with the thermostat (which can be thought of as consisting of infinitely many copies of our system — this is so-called canonical ensemble, characterized by N , V , T ). Here our system can have any energy and the question arises what is the probability W (E ). Let us find first the probability of the system to be in a given microstate a with the energy E . Assuming that all the states of the thermostat are equally likely to occur we see that the probability should be directly proportional to the statistical weight of the thermostat 0(E0 - E ) where we evidently assume that
 exp[S0(E0) − E/T)] and obtain
exp[S0(E0) − E/T)] and obtain
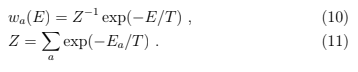
Note that there is no trace of thermostat left except for the temperature. The normalization factor Z (T , V , N ) is a sum over all states accessible to the system and is called the partition function. This is the derivation of the canonical distribution from the microcanonical one which allows us to specify The probability to have a given energy is the probability of the state (10) times the number of states.
Here (E ) grows fast while exp(- E /T ) decays fast when the energy E grows.
As a result, W (E ) is concentrated in a very narrow peak and the energy fluctuations around are very small (see Sect. 1.6 below for more details).
For example, for an ideal gas . Let us stress again that the Gibbs canonical distribution (10) tells that the probability of a given microstate exponentially decays with the energy of the state while (12) tells that the probability of a given energy has a peak.
An alternative and straightforward way to derive the canonical distribution is to use consistently the Gibbs idea of the canonical ensemble as a virtual set, of which the single member is the system under consideration and the energy of the total set is fixed. The probability to have our system in the state a is then given by the average number of systems a in this state divided by the total number of systems N . The set of occupation numbers {na} = (n0, n1, n2 . . .) satisfies obvious conditions
Any given set is realized in . number of ways and the probability to realize the set is proportional to the respective W .
14)
where summation goes over all the sets that satisfy (13). We assume that in the limit when the main contribution into (14) is given by the most probable distribution which is found by looking at the extremum of ln
Using the Stirling formula ln
we write ln and the extremum n*a corresponds to ln
which gives
(15)
The parameter β is given implicitly by the relation
(16)
Of course, physically ε(β) is usually more relevant than β (ε).
To get thermodynamics from the Gibbs distribution one needs to define the free energy because we are under a constant temperature. This is done via the partition function Z (which is of central importance since macroscopic quantities are generally expressed via the derivatives of it):
(17)
To prove that, differentiate the identity P
with respect to temperature which gives
equivalent to F = E - TS in thermodynamics.
One can also come to this by defining entropy. Remind that for a closed system we defined S = ln while the probability of state is wa = 1/
that is
FAQs on Phase Space, Micro-canonical, and Canonical - CSIR-NET Physical Sciences - Physics for IIT JAM, UGC - NET, CSIR NET
| 1. What is phase space in physics? |  |
| 2. What is the micro-canonical ensemble in statistical mechanics? |  |
| 3. What is the canonical ensemble in statistical mechanics? |  |
| 4. How are phase space, micro-canonical ensemble, and canonical ensemble related? |  |
| 5. How are phase space, micro-canonical ensemble, and canonical ensemble used in practical applications? |  |





















