The number 1 is special because it has only one factor, which is itself. It doesn’t meet the criteria to be classified as either a prime number (which has exactly two factors) or a composite number (which has more than two factors).
Playing with Numbers - 1 Class 6 Worksheet Maths
Q1: Fill ups:
(i) The numbers which have more than two factors are called ________.
Ans: Composite
A composite number has more than two factors. For example, 4 is a composite number because it has factors 1, 2, and 4.
(ii) The numbers which are not multiples of 2 are known as ________.
Ans: Odd
Odd numbers cannot be divided evenly by 2. For example, 3 and 7 are odd numbers because they don’t divide by 2 without leaving a remainder.

(iii) The two numbers which have only 1 as their common factor are called _________.
Ans: Co-primes
Co-prime numbers have no common factors other than 1. For instance, 8 and 15 are co-prime because 1 is their only common factor.
(iv) The number which is neither prime nor composite is _____.
Ans: 1
(v) Every number is a ________ and ________ of itself.
Ans: Factor, Multiple
Every number can divide itself exactly (making it a factor of itself) and can also be multiplied by 1 to get itself (making it a multiple of itself). For example, 5 is both a factor and a multiple of 5.
Q2: True or False:
(i) The sum of three odd numbers is even.
Ans: False
3 + 5 + 7 = 15, i.e., odd
(ii) The sum of two odd numbers and one even number is even.
Ans: True
3 + 5 + 6 = 14, i.e., even
(iii) The product of three odd numbers is odd.
Ans: True
3 x 5 x 7 = 105, i.e., odd
(iv) If an even number is divided by 2, the quotient is always odd.
Ans: False
4 ÷ 2 = 2, i.e., even
(v) All prime numbers are odd.
Ans: False
2 is a prime number and it is also even
(vi) Prime numbers do not have any factors.
Ans: False
1 and the number itself are factors of the number
(vii) The sum of two prime numbers is always even.
Ans: False
2 + 3 = 5, i.e., odd
(viii) 2 is the only even prime number.
Ans: True
(ix) All even numbers are composite numbers.
Ans: False
2 is a prime number
(x) The product of two even numbers is always even.
Ans: True
2 x 4 = 8, i.e., even

Q3: Answer the following Questions.
(i) Find all the multiples of 13 up to 100.
Ans: 13, 26, 39, 52, 65, 78, 91
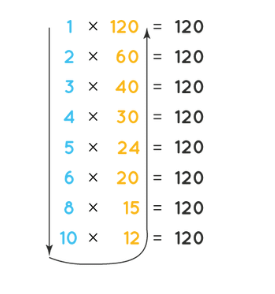
(ii) Write all the factors of 120.
Ans: 1, 2, 3, 4, 5, 6, 8, 10, 12, 15, 20, 24, 30, 40, 60, 120
(iii) Identify the numbers below which are multiples of 45.
270, 295, 305, 315, 333, 360, 400
Ans: 270, 315, 360
(iv) The numbers 13 and 31 are prime numbers. Both these numbers have same digits 1 and 3. Find such pairs of prime numbers up to 100.
Ans: 17, 71
37, 73
79, 97
(v) Write down separately the prime and composite numbers less than 20.
Ans: Prime numbers less than 20 are
2, 3, 5, 7, 11, 13, 17, 19
Composite numbers less than 20 are
4, 6, 8, 9, 10, 12, 14, 15, 16, 18
(vi) What is the greatest prime number between 1 and 10?
Ans: Prime numbers between 1 and 10 are 2, 3, 5, and 7. Among these numbers, 7 is the greatest.
(vii) Express the following as the sum of two odd primes.
(a) 44
(b) 36
(c) 24
(d) 18
Ans: (a) 44 = 37 + 7
(b) 36 = 31 + 5
(c) 24 = 19 + 5
(d) 18 = 11 + 7
(viii) Write seven consecutive composite numbers less than 100 so that there is no prime number between them.
Ans: Between 89 and 97, both of which are prime numbers, there are 7 composite numbers. They are
90, 91, 92, 93, 94, 95, 96
Numbers Factors:
- 90 = 1, 2, 3, 5, 6, 9, 10, 15, 18, 30, 45, 90
- 91 = 1, 7, 13, 91
- 92 = 1, 2, 4, 23, 46, 92
- 93 = 1, 3, 31, 93
- 94 = 1, 2, 47, 94
- 95 = 1, 5, 19, 95
- 96 = 1, 2, 3, 4, 6, 8, 12, 16, 24, 32, 48, 96
(ix) Write a digit in the blank space of each of the following numbers so that the number formed is divisible by 11:
(a) 92 ___ 389
(b) 8 ___9484
Ans:
(a) 92_389
Let a be placed in the blank.
Sum of the digits at odd places = 9 + 3 + 2 = 14
Sum of the digits at even places = 8 + a + 9 = 17 + a
Difference = 17 + a − 14 = 3 + a
For a number to be divisible by 11, this difference should be zero or a multiple of 11.
If 3 + a = 0, then
a = − 3
However, it cannot be negative.
The closest multiple of 11, which is near to 3, has to be taken. It is 11 itself.
3 + a = 11
a = 8
Therefore, the required digit is 8.
(b) 8_9484
Let a be placed in the blank.
Sum of the digits at odd places = 4 + 4 + a = 8 + a
Sum of the digits at even places = 8 + 9 + 8 = 25
Difference = 25 − (8 + a)
= 17 − a
For a number to be divisible by 11, this difference should be zero or a multiple of 11.
If 17 − a = 0, then
a = 17
This is not possible.
A multiple of 11 has to be taken. Taking 11, we obtain
17 − a = 11
a = 6
Therefore, the required digit is 6.
(x) A number is divisible by both 5 and 12. By which another number will that number be always divisible?
Ans: Factors of 5 = 1, 5
Factors of 12 = 1, 2, 3, 4, 6, 12
As the common factor of these numbers is 1, the given two numbers are co-prime and the number will also be divisible by their product, i.e. 60, and the factors of 60, i.e., 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30, 60.
(xi) A number is divisible by 12. By what other number will that number be divisible?
Ans: Since the number is divisible by 12, it will also be divisible by its factors i.e., 1, 2, 3, 4, 6, 12. Clearly, 1, 2, 3, 4, and 6 are numbers other than 12 by which this number is also divisible.
(xii) The product of three consecutive numbers is always divisible by 6. Verify this statement with the help of some examples.
Ans: 2 * 3 * 4 = 24, which is divisible by 6
9 * 10 * 11 = 990, which is divisible by 6
20 * 21 * 22 = 9240, which is divisible by 6
(xiii) The sum of two consecutive odd numbers is divisible by 4. Verify this statement with the help of some examples.
Ans: 3 + 5 = 8, which is divisible by 4
15 + 17 = 32, which is divisible by 4
19 + 21 = 40, which is divisible by 4
(xiv) Determine if 25110 is divisible by 45.
[Hint: 5 and 9 are co-prime numbers. Test the divisibility of the number by 5 and 9].
Ans: 45 = 5 * 9
Factors of 5 = 1, 5
Factors of 9 = 1, 3, 9
Therefore, 5 and 9 are co-prime numbers.
Since the last digit of 25110 is 0, it is divisible by 5.
Sum of the digits of 25110 = 2 + 5 + 1 + 1 + 0 = 9
As the sum of the digits of 25110 is divisible by 9, therefore, 25110 is divisible by 9.
Since the number is divisible by 5 and 9 both, it is divisible by 45.
(xv) Find the LCM of 12, 16, 24 and 36?
Ans:
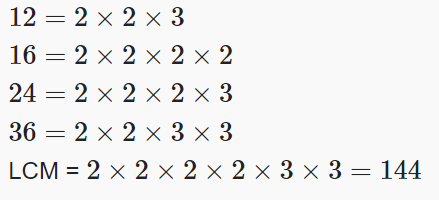
(xvi) Find the HCF of 70, 105, 175
Ans:
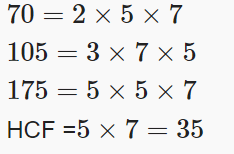
(xvii) You have 24 small bottles of lemonade and 36 large bottles. What is the largest number of equal-sized groups you can make if each group has the same number of small and large bottles?
Ans: 24 small bottles and 36 large bottles
HCF of 24 and 36 = 12
Largest number of equal-sized groups = 12
FAQs on Playing with Numbers - 1 Class 6 Worksheet Maths
| 1. What are prime numbers? |  |
| 2. How can we determine if a number is even or odd? |  |
| 3. How can we find the factors of a number? |  |
| 4. What is the significance of multiples of a number? |  |
| 5. How is the concept of divisibility important in mathematics? |  |

















