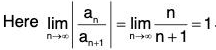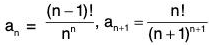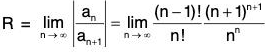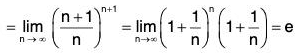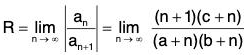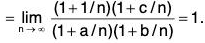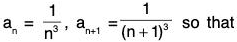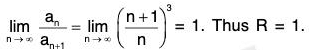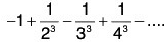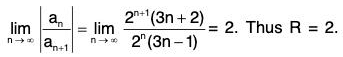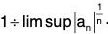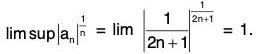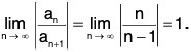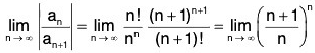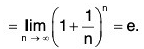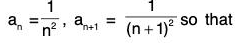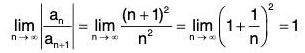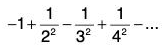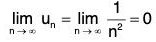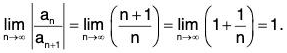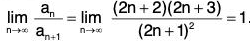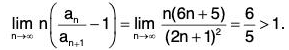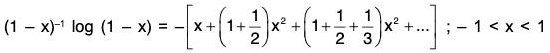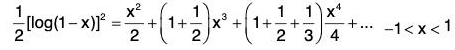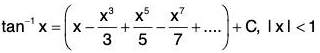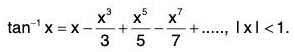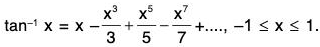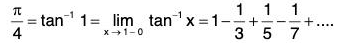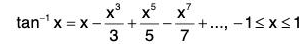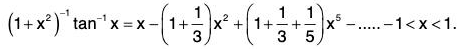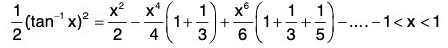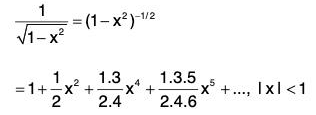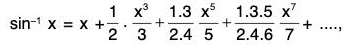Point Set Topology - III | Mathematics for Competitive Exams PDF Download
Interior And Exterior Of A Set
Interior Points of A Set
A point x is an interior point of a set S is S is a nbd of x. In other words, x is an interior point of S if ∃ an open interval (a, b) containing x and contained in S, i.e., x ∈ (a, b) ⊆ S.
Thus a set is a neighbourhood of each of its interior points.
Interior of A Set : The set of all interior points of set is called the interior of the set. The interior of a set S is generally denoted by Sj or into S.
Example : The interior of the set N or 1 or Q is the null set, but interior of R is R.
Example : The interior of a set S is a subset of S, i.e., Sj c S.
Interior, Exterior and Boundary of A Set
Definition :
(i) Let A be a subset of R and let p e A. Then p is called an interior point of A is there exists an e-nbd of p contained in A, i.e., if there exists an c > 0 such that ] p - ε, p - ε [ ⊂ A. The set of all interior points of A is called the interior of A and is denoted by Aº or by int A.
(ii) A point p is called an Exterior point of A if there exists an e-nbd of p contained in the complement A’ of A. The set of all Exterior points of A is called Exterior of A and is denoted by Ext A.
(iii) A point p is called a boundary point (or frontier point) of a if it is neither an interior nor an Exterior nor an Exterior point of A. The set of all boundary points of A called the boundary (or frontier) of A and is denoted by b (A) [or Fr(A)].
Result :
(i) Aº is the set of all those points of A which are not the limit points of A.’
(ii) A point p is an Exterior point of if and p is not an adherent point of A.
(iii) A point p is a boundary point of A if and only if every ε-nbd of p intersects both A and A’.
(iv) Aº is an open set,
(v) Aº is the largest open set contained in A
(vi) A is open if and only if Aº = A.
Theorem : Let A, B be any subsets of R Then
(i) Aº ⊂ A,
(ii) A ⊂ B ⇒ Aº ⊂ B°
(iii) (A ∩ B)° = A° ∩ B°
(iv) A° ∪ B° ⊂ (A ∪ B)°
(v) A°° = A°
Proof : We prove only (iii). The proofs of others are easy and let as Exercise for the reader. We have by (ii)
A ∩ B ⊂ A ⇒ (A n B)° ⊂ A° and A ∩ B ⊂ B ⇒ (A ∩ B)° ⊂ B.
(A ∩ B)° ⊂ A° ∩ B° ...(1)
Again A° ⊂ A and B° ⊂ B ⇒ A° ∩ B° ⊂ A ∩ B.
Also A° ∩ B° is open, being the intersection of two open sets.
Thus A° ∩ B° is an open set contained in A ∩ B. But (A ∩ B)° is the largest open set contained in A n B. Hence
A° ∩ B° ⊂ (A ∩ B)° ...(2)
From (1) and (2), (A ∩ B)° = A° ∩ B°
Compactness
(i) Open Cover of A Set : Definition : Let S ⊂ R and C = {AiI i ∈ I}, R be the group of open set in R. Then C is called the open cover of the set S, if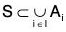
i.e., every element of S exist atleast is one of the open set of C.
(ii) Finite Subcover : Definition : Any finite subcover C’ = {Aj I j ∈ J ⊂ I}, S of open subcover C = {Ai I i ∈ 1} of any set S is called a finite subcover of S, if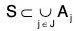
Example : Group C = {(- n, n) | n ∈ N} and C’ = {(- 3n, 3n) | n ∈ N} are two open covers of R and C’ is an open cover of C.
Example : Group of open intervals 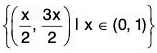 is the open cover of the set (0, 1).
is the open cover of the set (0, 1).
Compact Set : Definition
A non-empty subset of R is said to be compact if a finite subcover of S is contained in each open cover of any set S.
Example : A finite subset S = {x,, x2, xj of R is a compact set, since if C = {Ai I i ∈ 1} is an open cover of S, then for every xr ∈ S, there exist an open Ar in C, such that xr e Ar, r = 1, 2,.........n.
Now if C’ = {A I r = 1, 2 n}, then 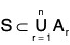
Therefore C’ is a finite cover of the set S.
Consequently, S is compact set.
Heine Borel (H-B) Theorem : Statement
Every open cover of a closed and bounded subset S of real number contains a finite subcover of S.
Proof. Let S be a closed and bounded subset of the set R of real numbers.
Now since S is bounded, therefore there exists an closed interval
l0 = [a, b] such that S ⊂ [a, b]
where a and b are the infimum and supremum respectively of S.
Let C = {Ai I i ∈ N} be an open cover of [a, b].
Hence C is also an open cover of S.
Therefore 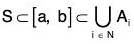
If possible, suppose no finite subcover of [a, b] is contained in C i.e., any finite sub group of C is not the subcover of l0 = [a, b].
Then bisecting 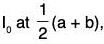 there will not exist finite subcover in C of atleast one of the intervals
there will not exist finite subcover in C of atleast one of the intervals 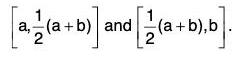
Denote this interval by l2 = [a2, b2].
Repeating this process, we get a sequence of nested intervals
I0 ⊃ I1 ⊃ I2 ⊃..... ⊃ I ⇒
in which no finite cover of any interval exist in C.
Clearly, Length of I = IInI = bn - an = 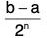
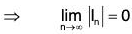
Therefore by the property of nested intervals, there exist only one point say x0 in 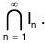 This point x0 exists in each of the above nested interval, therefore x0 ∈ [a, b]. But C is the open cover of [a, b]. Therefore for x0, there exists an open set say A0 in C such that x0 ∈ A0. Now since A0 is an open set, therefore x0 ∈ A0 ⇒ ∃ε > 0 s.t. (x0 - ε x0 + ε) ⊂ A0.
This point x0 exists in each of the above nested interval, therefore x0 ∈ [a, b]. But C is the open cover of [a, b]. Therefore for x0, there exists an open set say A0 in C such that x0 ∈ A0. Now since A0 is an open set, therefore x0 ∈ A0 ⇒ ∃ε > 0 s.t. (x0 - ε x0 + ε) ⊂ A0.
Again, since lim IInI = 0, therefore a natural number k may be chosen such that b 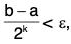 then lk ⇒ (xo - ε, x0 + ε) c A0
then lk ⇒ (xo - ε, x0 + ε) c A0
Consequently, there will be a finite cover of one element of the interval lk in C. This is contrary to the fundamental property of the above intervals l0, I1, l2, ... .
Thus our assumption is false.
Therefore there exist a finite cover of [a, b] in C.
Hence finite cover of S is also in C.
The above theorem can also be stated as follows:
Alternative definition of Compact set
A non-empty subset of R is said to be compact if it is closed and bounded.
Properties of Compact Sets
Theorem : Every compact subset of real numbers is closed and bounded. A subset of real numbers is compact iff it is closed and bounded.
Proof. S is bounded :
Let S be the compact subset of R and An = (- n, n), then
C = {An I n ∈ N}
is an open cover of R. Hence this is also an open cover of S.
Since S is a compact set, therefore there exist finite natural numbers n1, n2, ..., nk such that finite subgroup { An1, A n2,.. . . Ank } of C will also be subcover of S. Let n0 = max {n1, n2...... nk}, then clearly,
S ⊂ An0 = ( - n0,n0)
Consequently, S is a bounded set.
S is closed :
For this we shall show that no point of R - S is limit point of S i.e. all the limit points of S exist in S itself.
Therefore let a ∈ R - S, then a ∉ S. For every n ∈ N,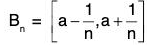 is a closed set. ⇒ R - Bn is an open set.
is a closed set. ⇒ R - Bn is an open set.
⇒ C’ = (R - Bn I n ∈ N} is a group of open set.
Again, clearly 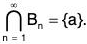 Now since a ∉ ( S , therefore
Now since a ∉ ( S , therefore
S ⊂ [R - ∩ Bn : n ⊂ N] = ∪ [R - Bn : n ∈ N] [By Demorgan’s law]
⇒ C’ is a cover of S
But S is a compact set, therefore by the compactness property, there will exist finite natural numbers m1, m2, .... ms such that each point of S will exist atleast in one of
R - Bm1, R - Bm2 ,...., R - Bms
Therefore if x ∈ S, then
x ∈ S ⇒ 3 i ∈ {1, 2, 3, .... r} r.t. x ∈ R - Bm1
⇒ any point of S does not exist in 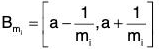
⇒ a is not the limit point of S ⇒ all the limit points of S exist in S.
⇒ S is closed
Theorem. R is not compact.
Solution. Let An = (- n, n), then An is an open set for each value of natural number and C = {An I n ∈ N} is the open cover of R,
because 
If C' = {An1, An2 ,......., Ank}
be the finite subgroup of the cover C, then let
n0 = max {n1, f n2...., nk}
then n0 ∉ An, ∀ i = 1, 2, .... k.
Therefore clearly, any finite subset of C can not be the cover of R.
Consequently, R is not compact.
Theorem : No open interval (a, b) is compact.
Solution. Let An 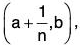 then for every natural number n, An is an open set and C = {An I n ∈ N} is an open cover of (a, b) since (a, b) ⊂
then for every natural number n, An is an open set and C = {An I n ∈ N} is an open cover of (a, b) since (a, b) ⊂ 
Now we will show that no finite subgroup of C can not be the subcover (a, b). If
C' = { An1, An2 ,...., Ank}
be the finite subgroup of the cover C, then let n0 = max { n1, n2, ..., nk} then clearly, 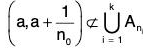
Therefore C’ can not be the subcover of (a, b).
Consequently, (a, b) is not compact.
Cantor Ternary Set : [г]
I Stage : Denote the closed interval [0, 1] by F0.
Divide the interval into three equal parts and remove the middle one third open interval l1,1 = 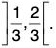
Remaining two disjoint open intervals 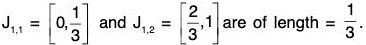
Now J1,1 U J1,2 = F1 (say)
II Stage : Now again divide the above two closed intervals J . . and J, 2 into three equal parts and remove the middle one third open intervals of each of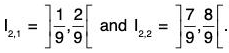
Thus there remains the following four (22) disjoint closed intervals :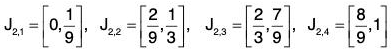
The length of each of the above interval = 1/9
Now J2,1 U J2,2 U J2,3 U J2,4 = F2 (say) ...(2)
and O2 = l2,1 U l2,2
nth Stage :
In the nth stage (2n-1) open intervals ln,1, ln,2,...,ln,2n - 1 , will be removed and there remains 2n closed intervals ln,1, ln,2, In,2n (left to right) where length of each subinterval = 
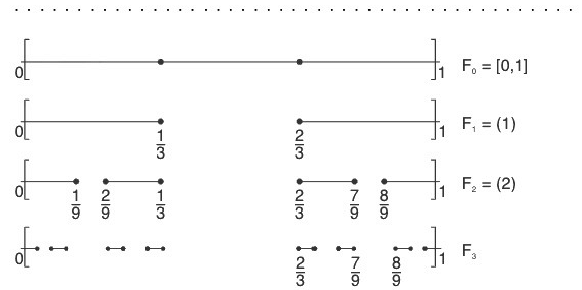
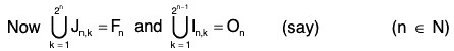
Now the set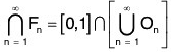 is called Cantor’s theory sat and is denoted by Γ'.
is called Cantor’s theory sat and is denoted by Γ'.
Remark. The set T is non-empty because the end points of the closed intervals have not been removed and are in the set T.
Connectedness
Connected Set. Definition : A subset S of the set of real numbers R is called connected set if no two disjoint open sets A and B of R exist such that
S ⊂ A ∪ B and A ∩ S ≠ ϕ, B ∩ S ≠ ϕ
The set which is not connected, is known as Disconnected Set.
Example 1 : S = {x ∈ R I 0 < x < 1} is a connected set because no two disjoint subsets A and B of R such that
S ⊂ A ∪ B and A ∩ S ≠ ϕ), B ∩ S ≠ ϕ
Example 2 : Each open interval (a, b) is a connected set.
Theorem : Any subset S of real numbers is a connected set iff S is an interval.
Proof. S is connected ⇒ is an interval :
If possible, let S be not an interval, then there will exist three real numbers a, q, b such that a < q < b and a g S. b ∈ S but q ∉ S.
Clearly, a ∈ (- ∞, q) = A (say), b e (q, ∞) = B (say)
Therefore there exist non-empty open sets A and B such that
A ∩ B = ϕ, S ⊂ A ∪ B, S ∩ A, ≠ 4. S ϕ. B = ϕ
Consequently, S is not a connected set.
Therefore, if S is not an interval, then this will not be a connected set.
Conversely : Set S is an interval ⇒ S is connected
Let S be an interval and A, B be two open sets such that
A ∩ S ≠ ϕ, B ∩ S ≠ ϕ and A ∩ B = ϕ
Let a ∈ A ∩ S and b ∈ S ∩ S. since a ≠ b,
Therefore, let a < b then [a, b] will be a subinterval of the set S.
Let u be the supremum of the set A ∩ [a, b].
Since a, b are internal points of A and B respectively
and A ∩ B = ϕ, therefore a < u < b
Now if ε > 0 is a number such that a < u - ε < u + ε < b
then there will be atleast one point of A in (u - ε, u)
and no point of A will be there in (u, u + ε).
Consequently, (u - ε, u + ε) is not the subset of the sets A or B.
Again, since A and B are open, therefore u ∉ A and u ∉ B.
S ⊄ A ∪ B
⇒ S is a connected set.
Therefore S is connected ⇒ S is an interval.
Theorem : The set R of real numbers is a connected set.
Proof. If possible, let R be not connected set then there exist two disjoint open sets A and B such that
R ⊂ A U B and A ∩ R ≠ ϕ, B ∩ R ≠ ϕ)
Let a ∈ A, b ∈ B and
A1 ={x ∈ [0, 1] :a + x(b - a) ∈ A}
and B1 = {x ∈ [0, 1] : a + x(b - a) ∈ B}
Now since [a, b] = {α = a + s(b - a) : 0 < x < 1} ⊂ R ⊂ A ∪ B
∴ A1 ∪ B1, = [0, 1]
Again since a ∈ A and a = a + 0(b - a) ⇒ 0 ∈ A, ⇒ A. ≠ ϕ
Similarly, b ∈ B and b = a + 1(b - a) ⇒ 1 ∈ B1 ⇒ B1 ≠ ϕ
Since A, B are two disjoint open sets, therefore At and Bt are also two disjoint open sets. Consequently {A,, B,} shows the disconnectivity of the interval [0, 1] which contradicts the statement of the theorem proved earlier.
Therefore our earlier assumption is false i.e., R is a connected set.
Example 32: That the only subsets of R which are both open and closed are R and ϕ.
Let A be a subset of R which is both closed as well as open.
Then ~ A = R - A = B (say) will also be open as well as closed.
If A ≠ ϕ and A ≠ R, then there exist two non empty disjoint subsets A and B such that
R ⊂ A ∪ B, A ∩ R ≠ ϕ, B ∩ R ≠ ϕConsequently, R will not be connected set which contradicts the above theorem.
Therefore A = ϕ or R.
i.e., ϕ and R are the only two subsets of R which are both open and closed.
Power Series
Definition 1: A series of the form 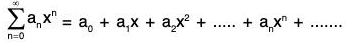
where a0,a1,a2,.......are constant, is called a power series in x.
Definition 2 : A constant R > 0 such that Σan(x - x0)n converges for I x - x0l < R and diverges for I x - x0 I > R is called the radius of convergence of the series.
Interval (domain) of Convergence
The interval l x l < R or - R < x < R is called the interval (domain) of convergence.
Examples
1. 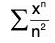 converges when I x I < 1 and diverges when I x I > 1.
converges when I x I < 1 and diverges when I x I > 1.
Radius of Convergence
The radius of convergence is a number R such that the series
Σan(x - x0)n
converges absolutely for lx - x0I < R and diverges for lx - x0l > R
Note that :
- If the series converges ONLY at x = x0, R = 0.
- If the series converges for ALL values of x, R is said to be infinite
Formula for The Radius of Convergence
If the power series ΣXanxn is such that an ≠ 0 for all n and 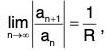 then ΣXanxn is convergent (absolutely convergent) for I x I < R and divergent for I x I > R.
then ΣXanxn is convergent (absolutely convergent) for I x I < R and divergent for I x I > R.
OR
The radius of convergence R of a power series Σan xn may be determined by the following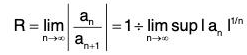
R = ∞, when lim I an l1/n = 0
R = 0, when lim I an l1/n = ∞
Example 33: Find the radius of convergence of 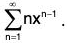
Hence the radius of convergence = 1.
Example 34: Find the radius of convergence of the series
∴
Hence the radius of convergence = e.
Ex. Find the radius of convergence and the exact interval of convergence of the following power series :
(i)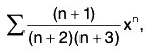
(ii)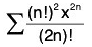
Ans. (i) 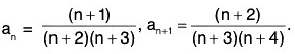
∴ 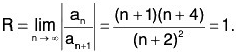
Thus the given series converges for I x I < 1 and diverges for I x I > 1. We now check at the end points x = 1, -1.
For x = 1, the nth term of the series is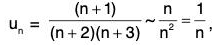
However for x = -1, the given series is an alternating series for which ur+1 < u_ V n and lim un=0. Thus, by Leibnitz’s test, the series converges for x = -1. Hence the interval of
n-**
convergence is [-1, 1[.
(ii) Given 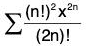
Let x2 = y
then power series reduces to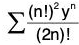
We have 
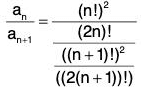
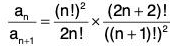
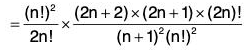
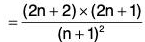
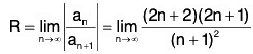
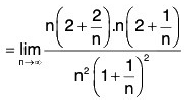
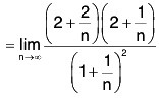
= 4
So the power series converges for I y I < 4 i.e. Ixl2<4 ⇒ l x l < 2 and diverges for I y I > 4. i.e. I x I2 > 4. So the interval of convergence is I x I < 2 i.e. (- 2, 2). And Radius of convergence is 2.
Example 35: Prove that the power series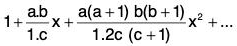
has unit radius of convergence.
(omitting the first term)
∴
Example 36: Find the domain of convergence of the series
(i) 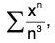
(ii) 
(i)
For x = 1, the given power series iswhich is convergent.
For x = -1, the given power series iswhich is convergent, by Leibnitz’s Test.
Hence the domain for convergence is [-1, 1].
(ii) The given power series is about the point x = 1. We have
The domain of convergence of the given power series is
-2 + 1 < x < 2 + 1 or -1< x < 3.
For x = 3, given power series iswhich is convergent by Leibnitz’s Test.
Hence the domain of convergence of the given power series is -1 < x < 3.
Example 37: Determine the interval of convergence of
(i) 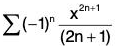
(ii) 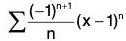
(iii) 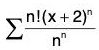
(i) an is coefficient of xn. Thus an = 1/(2n+1) is wrong. Actually a2n+1 = 1/(2n+1) and an = 0 whenever n is even. Thus, we apply R =
Hence, R = 1.
The interval of convergence is (-1, 1).
For x = 1, the series becomeswhich is convergent by Leibnitz’s test.
For x = -1, the series becomeswhich is again convergent.
Hence the Exact interval of convergence is [-1, 1].
(ii)∴ R = 1.
Since the given power series is about the point x = 1, the interval of convergence is -1 + 1 < x < 1 +1 or 0 < x < 2.
For x = 2, the given series iswhich is convergent by Leibnitz’s Test.
Hence the exact interval of convergence is (0, 2].
(iii) The given power series is about the point x = -2.
R = e and the interval of convergence is (- 2 - e, -2 + e).
Theorems of Power Series
Theorem : If a power series Σan xn converges for x = x0, then
(i) it is absolutely convergent in the interval I x I < I x0 I
(ii) it is uniformly convergent in the interval I x I < I x. I, where I x1 I < I x0 I.
Proof. (i) Since Σan x0n converges, so 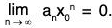
Consequently there exists a positive integer m such that ... (1)
... (1)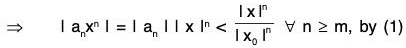
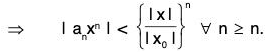
The series on the R.H.S. converges for I x I < I x01 (being a geometric series with common ratio < 1), it follows by the comparison test that Σ I anxn I is convergent for I x0 I < I x0 I.
Hence Σ an xn is absolutely convergent for I x I < I x0 I.
(ii) Let 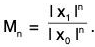 Then Σ Mn converges, since I x1 I < I x0 I (being a geometric series with common ratio < 1).
Then Σ Mn converges, since I x1 I < I x0 I (being a geometric series with common ratio < 1).
Using (1), we obtain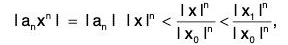
I anxn I < Mn ∀ n > m, where Σ Mn converges.
By the Weierstrass M-test, Σanxn is uniformly convergent in I x I < I x1 I.
Note : If a power series whose radius of convergence is 1, then it converges absolutely (- 1, 1) and uniformly in [- k, k], | k | < 1.
Theorem : If a power series ΣXanxn converges for I x I < R, then it converges uniformly on [- R + ε, R - ε], for each ε > 0.
Proof. Let x0 = R - ε < R so that Σanx0n converges absolutely.
For I x I < x0, I anxn I < I an I x0n.
Since Σanx0n converges absolutely, therefore, by Weierstrass’s M-test, the series Σanx0n converges uniformly on
[-x0, x0] = [-R + ε, R - ε].
Hence the theorem.
Theorem : Suppose a power series Σanxn converges for I x I < R and that f(x) = Σan xn. Then
(i) f(x) is continuous in (—R, R).
(ii) Σanxn can be integrated term by term on (—R, R) and the integrated series has the same radius of convergence as Σanxn
(iii) Σanxn can be differentiated term and term on (-R, R) and f(x) = Σn anxn-1 I x I < R. Further the differential series has the same radius of convergence as Σanxn.
Proof, (i) Since each term of the power series Σanxn is continuous in (—R, R) and the series is uniformly convergent on (-R, R), so the sum f(x) of the given series is continuous in (-R, R)
(ii) Since each term of X anxn is continuous in (-R, R) and Σanxn converges uniformly to f(x) in (-R, R), so Σ an xn can be integrated term by term in (-R, R) and the integrated series is 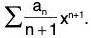 Further
Further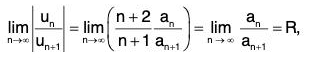
which shows that ∑anxn and 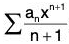 have the same radius of convergence.
have the same radius of convergence.
(iii) We know each term of Z anxn is continuous, has continuous derivative in (-R, R) and ∑anxn is uniformly convergent in (-R, R). Thus the series obtained by differentiating the power series ∑anxn is ∑anxn-1 Further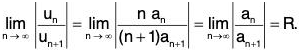
Hence the differentiated series Σn anxn-1 is also a power series which has the same radius of convergence as Ian Σanxn.
Note. If f(x) = Σanxn, then f(x) is called the sum function of the series.
Abel’s Theorem : If a power series converges at an end point of its interval of convergence, then the power series is uniformly convergent in the interval which includes this end point.
Remarks : If a power series with interval of convergence (-R, R) converges at both the endpoints - R and R, then the power series is uniformly convergent in [- R, R].
Theorem : If a power series converges at the end-point x = R of the interval of convergence (-R, R), then it is uniformly convergent in (-R, R] or [-R + e, R] where c > 0. In particular, the series is uniformly convergent in [0, R],
Abel’s Limit Theorem : Let Σan xn be a power series with finite radius of convergence R such that f(x) = Ean xn - R < x < R. If the series Ean Rn converges, then
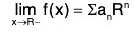
Theorem : (Cauchy’s product of two power series)
Two power series 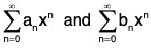 can be multiple to obtain the power series
can be multiple to obtain the power series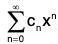 where
where
cn = a0 bn + a1 bn-1 + a2 bn-2 , + + an bn
the result being valid for each x within the common interval of convergence.
Example 38: Show that the series Exn/n2 is uniformly convergent in [-1, 1].
We have
The radius of convergence is R = 1 and so the given series is uniformly convergent in (-1, 1).
For x = 1, given series iswhich is convergent.
For x = -1, given series becomes
This is an alternating series for which un + 1, < un ∀ n and
So by Leibnitz’s test, the series to convergent for x = -1. Hence by Abel’s Theorem, given power series is uniformly convergent in [-1, 1].
Example 39: Show that the series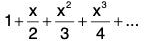
is uniformly convergent in [-1, k], 0 < k < 1.
We have
The radius of convergence is R = 1 and so the given series is absolutely convergent in ]-1, 1[.
For x = 1, given serieswhich is divergent.
However for x = 1, given series becomeswhich is convergent by Leibnitz’s Test. Hence by Abel’s Theorem, given power series is uniformly convergent [-1, 1[ or [-1, k], where 0 < k < 1.
Example 40: Show that the following series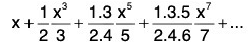
is uniformly convergent in [-1, 1].
Ignoring the first term, we have
∴
Since the radius of convergence is R = 1, given power series is absolutely convergent in (-1, 1). For x = 1, we see that the D’Alembert's ratio test fails. Now
By Raabe’s test, the series is convergent for x = 1.
Again for x = -1, the series is convergent.
(∵ ∑an is convergent ⇒ ∑an is convergent)
Hence the given power series is uniformly convergent in [-1, 1] (Abel’s Theorem).
Example 41: Prove that 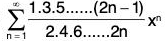 is uniformly convergent in [-1, 1).
is uniformly convergent in [-1, 1).
Both the series given on the R.H.S. of (1) and (2) absolutely convergent in (-1, 1), so their Cauchy’s product converge to (1 - x)-1 log (1 - x). Thus
Integrating, we get
where the constant of integration vanishes.
Since the series on the right converges at x = -1, so by Abel’s theorem, the above Expansion is valid for -1 < x < 1.
Example 42: Show that
(i) 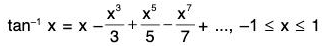
(ii) 
(iii) 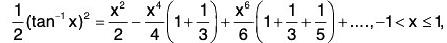
We have
(1 + x2)-1 = 1 - x2 + x4 - x6 + I x I < 1. ...(i)
Radius of convergence is
Thus the series is convergent absolutely for all x such that I x I < 1, and is uniformly convergent in [-k, k], | k | < 1.The integrated series is also convergent absolutely in (-1, 0) and uniformly in [-k, k], | k | < 1. Integrating (1), we get
where C is constant of integration.
Putting x = 0, we get C = 0 and so
Now the seriesis convergent at x = ±1.
is an alternating series which converges, by Leibnitz’s test.
Similarly it is convergent for x = -1].
By Abel’s theorem, it is uniformly convergent in [-1, 1].
Hence
(ii) Putting x = 1, by Abel’s limit theorem,
(iii) We have
and (1 + X2)-1 = 1 - x2 + x4 - x6 +..., -1 < x < 1.
By part (i), both the series are absolutely convergent in (-1, 1), so they can be multiplied and their Cauchy’s product will be equal to
integrating, we get
Here is the constant of integration vanishes on taking x = 0.By Leibnitz’s test, the series on the R.H.S. converges for x = 1. Hence the above expansion is valid for -1 < x < 1.
Example 43: Show that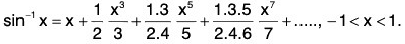
Deduce that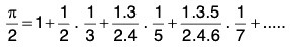
We know that
The series on the R.H.S. is a power series with radius of convergence 1 and so it is absolutely convergent in(-1, 1) and uniformly convergent for [-k, k], | k | < 1. The integrated series is also convergent in (-1, 1) and uniformly convergent for [-k , k], | k | < 1. integrating, we get
Putting x = 0, we get c = 0....(1)
For x = 1, the nth term of the series on the R.H.S. of (1) is
∴
So by Raabe’s test, the series is convergent for x = 1. Hence
(ii) At x = 1, by Abel’s limit theorem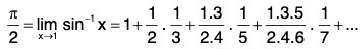
Ex. Prove that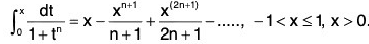
Example 44: For n > 0, we have
(1 + tn)-1 = 1 - tn + t2n - t3n +....
It is clear that the series on the right has its radius of convergence R = 1.
By Theorem this series can be integrated term by term on (-1, 1) and the integrated series will also have the radius of convergence as unity. Thus
...(1)
At x = 1, the series on the right is convergent, by Leibnitz’s test.
Hence (1) is true for -1 < x < 1.
Theorem (Differentiation of Power Series)
Let a power series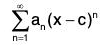
have non-zero radius of convergence R and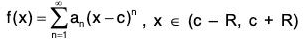
Then, the following holds :
The function f is differentiable on the interval (c - R, c + R). Further the series 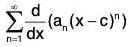 also has radius of convergence R and f(x) =
also has radius of convergence R and f(x) = 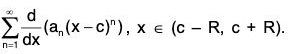
The function f has derivatives of all orders and 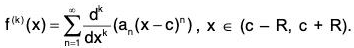
Theorem (Integration of Power Series)
Let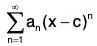
be a power series with non-zero radius of convergence R and let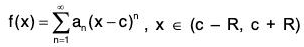
Then
(i) The function f has an anti derivative F(x) given by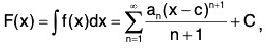
where C is an arbitrary constant and the series on the right hand side has radius of convergence R.
(ii) For [α, β] ⊂ (c - R, c + R),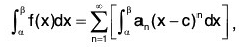
where the series on the right hand side is absolutely convergent.
Example : Consider the power series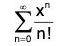
By the ratio test, for every x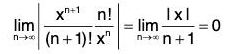
Hence, the series is absolutely convergent for every x. Let
Then, f is differentiable by theorem and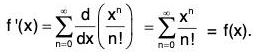
Some Important Power Series
Consider the following power series :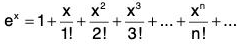

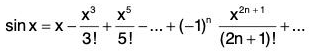
For the first series,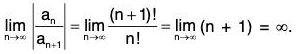
Theorem : Define cosine and sine functions as sums of power series. Prove that
(i) S(x + y) = S(x)C(y) + C(x)S(y),
(ii) C(x + y) = C(x)C(y) - S(x)S(y),
where C, S denote cosine and sine respectively.
Proof. The cosine function is defined as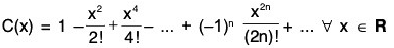 ...(1)
...(1)
The sine function is defined as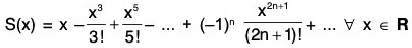 ...(2)
...(2)
These two power series are uniformly convergent ∀ x ∈ R and consequently, the functions C(x) and S(x) are continuous ∀ x ∈ R
Differentiating term by term the convergent series (2),
which gives us the uniformly convergent series (1),
Thus S(x) is derivable, and S’(x) = C(x). ...(3)
Similarly C’(x) = -S(x). ...(4)
From (1) and (2); S(0) = 0 and C(0) = 1. ...(5)
Let y be any arbitrary but fixed real number. We write
f(x) = S(x + y) - S(x)C(y) - C(x)S(y), ...(6)
g(x) = C(x + y) - C(x)C(y) + S(x)S(y). ...(7)
Differentiating w.r.t. x, we obtain
f(x) = C(X + y) - C(x)C(y) + S(x)S(y) = g(x).
g’(x) = -S(x + y) + S(x)C(y) + C(x)S(y) = -f(x). [Using (3), (4)]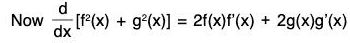
= 2f(x)g(x) - 2g(x)f(x) = 0 ∀ x ∈ R
It follows that f2(x) + g2(x) is a constant ∀ x ∈ R
⇒ f2(x) + g2(x) = f2(0) + g2(0) ∀ x ∈ R
= [S(y) - S(0)C(y) - C(0)S(y)]2 + [C(y) - C(0)C(y) + S(0)S(y)]2 = 0 [Using (5)],
f2(x) + g2(x) = 0, ∀ x ∈ R implies that f(x) = 0 and g(x) = 0.
Hence (6) and (7) yield
S(x + y) = S(x)C(y) + C(x)S(y),
C(x + y) = C(x)C(y) - C(x)S(y).
Corollary 1. S(-x) = -S(x) ; C(-x) = C(x) ∀ x ∈ R
We have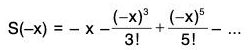
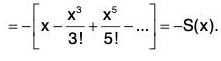
Similarly we can prove the second part.
Corollary 2. S(x - y) = S(x)C(y) - C(x)S(y),
C(x - y) = C(x)C(y) + S(x)S(y).
Replacing y by - y in (i) and (ii) of Theorem
S(x - y) = S(x)C(-y) + C(x)S(-y),
C(x - y) = C(x)C(-y) - S(x)S(-y).
The desired results follow by Corollary 1.
Corollary 3. C2(x) + S2(x) = 1 or cos2x + sin2 x = 1 ∀ x ∈ R
We have 1 = C(0) = C(x - x)
= C(x)C(-x) - S(x)S(-x)
= C2(x) + S2(x), by Corollary 1
Hence cos2 x + sin2 x = 1 ∀ x ∈ R
Corollary 4. I C(x) I < 1, I S(x) I < 1. ∀ x ∈ R
I cos x I < 1, I sin2 x I < 1 ; ∀ x ∈ R
This follows by Corollary 3.
Corollary 5. sin 2x = 2 sin x cos x, cos 2x = cos2 x - sin2 x.
Replacing y by x in (i) and (ii) of Theorem we obtain
S(2x) = 2S(x) C(x), C(2x) = C2(x) - S2(x)
Hence the results follows.
Remark. It may be noted that the above properties of C(x) and S(x) are similar to those of the trigonometric functions cos x and sin x respectively. Thus we have
C(x) = cos x and S(x) = sin x.
Theorem : Define cos x as a power series and determine its domain. Prove that there exists a least positive number π such that cos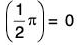
Proof. cos x is defined as the sum of the power series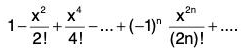
Its radius of convergence is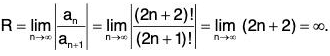
Thus this power series is convergent for ∀ x ∈ R and so the domain of cos x is R.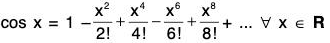 ...(1)
...(1)
∴ cos 0 = 1 > 0 and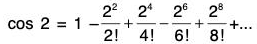
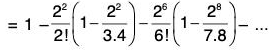
Since the brackets are all positive, therefore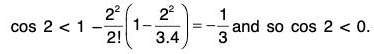
Thus we see that cos x is a continuous function in the closed interval [0, 2], where cos 0 and cos 2 are of opposite signs. By Intermediate value theorem, there exist at least one number α ∈ ]0, 2[ such that cos α = 0. We now proceed to show that α is unique.
Let, if possible, β ∈ (0, 2) satisfy cos β = 0 so that
cos α = cos β = 0, 0 < α, β < 2.
By Rolle’s theorem, there exists some number λ, α < λ < β, such that - sin λ = 0.
∴ sin λ = 0, 0 < λ < 2. ...(2)
By definition,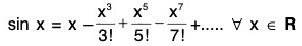
∴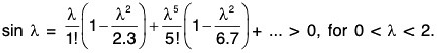
This contradicts (2).
Thus there exists one and only one root of the equation cos x = 0 lying between 0 and 2. i.e., cos α = 0, 0 < α < 2.
We denote α as 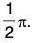 Hence
Hence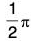 is the least positive root of the equation cos x = 0 i.e., cos
is the least positive root of the equation cos x = 0 i.e., cos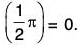
Also, therefore, we have cos x > 0 when 0 < x < 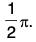
Theorem : Define Exponential function E(x) as the sum of a power series. Show that the domain is the set of all real numbers. Prove that
E(x + y) = E(x)E(y) for all x, y ∈ R.
If e denote E(1), prove that E(x) = Ex for all real x.
Proof. The Exponential function E(x) is defined as the sum of the power series ...(1)
...(1)
We have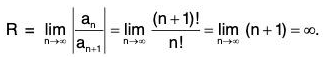
Thus the radius of convergence of the above power series is R = oo so that the power series is everywhere convergent i.e., E(x) is defined ∀ x ∈ R. This shows that the domain of the Exponential function is R.
It is clear that the function E(x), defined by (1), is continuous and has derivatives of all orders, for each x ∈ R.
Differentiating (1), we get
E’(x) = E(x) and so E”(x) = E(x), E’”(x) = E(x) etc.
in fact E(n)(x) = E(x) ∀ n ∈ N.
By Taylor’s Theorem, for all real values t and x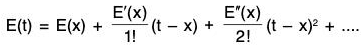
or 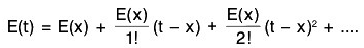
Replacing t by x + y, we get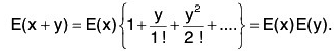
Thus E(x + y) = E(x) E(y) ∀ x, y ∈ R. ....(2)
From (1), 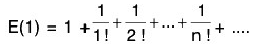
The above series on the right converges to a number which lies between 2 and 3. We denote this number by e so that E(1) = e.
The property (2) can be Extended as
E(x1 + x2 +... + xn) = E(x1) E(x2) ... E(xn) ...(3)
for any positive integer n and ∀ x ∈ R.
Taking x1 = x2 = ... = xn = x in (3), we obtain
E(nx) = {E(x)}n ∀ x ∈ R, ∀ n ∈ N. ...(4)
For x = 1, we obtain
E(n) = en ∀ n ∈ N (∵ E(1) = e) ...(5)
Taking x = m/n (m and n being positive integers) in (4),
E(m) = {E(m/n)}n or em = {E(m/n)}n, by (5)
E(m/n) = (em)1/n = em/n.
Thus E(q) = eq for all positive rationals q. ...(6)
Let x be any positive irrational number. Then there always exists a sequence {xn} of positive rational numbers such that xn → x.
Using (6), E(xn) = exn ∀ n ∈ N.
Since xn → x as n → ∞ and E is a continuous function ∀ x ∈ R, therefore
E(x) = ex for all positive irrationals. ...(7)
From (6) and (7), we conclude that
E(x) = Ex for all positive reals. ...(8)
Taking y = - x in (2), we get
E(0) = E(x)E(-x) or 1 = E(x) E(-x) (x > 0) [∵ E(0) = 1, by (1)]
or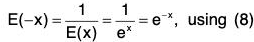
Hence E(x) = Ex ∀ x ∈ R.
Theorem : Let f be a continuous function on R such that
f(x + y) = f(x) + f(y) ∀ x, y ∈ R. ...(1)
Show that f(x) = cx for some constant c and ∀ x ∈ R.
Proof. Putting y = x in (1), f(2x) = 2f(x).
In fact f(nx) = nf(x) ∀ x ∈ R, ∀ n ∈ N.
Replacing x by x/n, we get
f(x) = nf(x/n) or f(x/n) = (1/n) f(x) ∀ x ∈ R.
For any integers p and p(q > 0), it follows that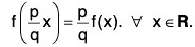
Thus f(rx) = r f(x), for any rational number r. ...(2)
Let us write f(1) = e. Taking x = 1 in (2), we get
f(x) = cr, for every rational number r. ...(3)
Let a be any irrational number. Then there exists a sequence {rn} of rational numbers such that rn → a
=> f(rn) → f(a), by continuity of f
=> f(a) = lim f(rn) = lim crn = c lim rn = ca, using (3).
Hence f(x) = cx ∀ x ∈ R.
Theorem : Let f be a non-zero continuous function on R such that
f(x + y) = f(x) f(y) ∀ x, y ∈ R. ...(1)
Show that f(x) = ecx, for some constant c ≠ 0.
Proof. It is given that f(x) ≠ 0 ∀ x ∈ R. From (1),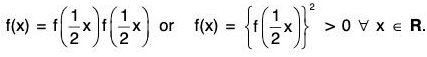
Let g(x) = loge f(x) ∀ x ∈ R. Then by (1),
g(x + y) = g(x) + g(y) ∀ x, y ∈ r. ...(2)
Now g, being the composition of two continuous functions f(x) and loge x, is itself continuous on R and g satisfies (2).
By Theorem, it follows that
g(x) = cx ∀ x ∈ R, c being a constant
⇒ logef(x) = cx f(x) = ecx ∀ x ∈ R.
Theorem : Let f be a non-zero function continuous on R+ such that f(xy) = f(x) + f(y) ∀ x, y > 0. ...(1)
Show that f(x) = loga x, x ∈ R+ (a > 0, a ≠ 1).
Proof. For x > 0, let us take t = loge x o x = e', t e R ...(2)
Let g(t) = f(e') V t e R. Then g is continuous on R and
g(t + s) = f(e,+s) = f(e:es) + f(es) by (1)
or g(t + s) = g(t) + g(s).
Here t, s e R. By Theorem g(t) = ct, V t e R, c being a constant.
Thus f(x) = c loge x V x e R+, where c ≠ 0 as f is non-zero.
Let a = e1/s. Then f(x) = loga x V x e R+ (a > 0, a ≠ 1).
Taylor Series and Maclaurin Series
Definition : Let f : I = (a - 5, a + 8) -> R be a function which has derivation of all order in I. Then the power series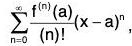
is called the Taylor series for f at x = a. We say f has Taylor series Expansion at x = a, if its Taylor series is convergent for x e I and its sum is f(x). For a = 0, the Taylor series for f is called the Maclaurin Series for f at x = 0.
Example : For the function  its derivatives of all order exist in domain
its derivatives of all order exist in domain
I = (- ∞, 0) U (0, ∞)
For a = 1, since
f(n) (x) = (- 1)n n!x- (n + 1)
we have
f(n) (1) = (- 1)n n!, ∀ n > 1
Thus
n-0
is its Taylor series at x = 1. Since it is a geometric series, it will be convergent if I x - 1 | < 1 i.e., 0 < x < 2.
Further, its sum is
Hence, 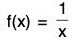 has Taylor series Expansion
has Taylor series Expansion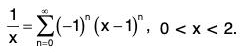
|
98 videos|34 docs|32 tests
|
FAQs on Point Set Topology - III - Mathematics for Competitive Exams
| 1. What is point set topology? |  |
| 2. What are some important concepts in point set topology? |  |
| 3. How is point set topology relevant to the IIT JAM exam? |  |
| 4. Can you give an example of a problem related to point set topology? |  |
| 5. How can one prepare for the point set topology section of the IIT JAM exam? |  |