Point Slope Form and Two Point Form | Mathematics (Maths) Class 11 - Commerce PDF Download
C. Standard Equations of Straight Lines
(1) General Form : Any first degree equation of the form Ax + By + C = 0, where A, B, C are constant always represents general equation of a straight line (at least one out of A and B is non zero.)
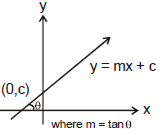
(2) Slope - Intercept Form :
y = mx + c
where m = slope of the line = tanθ
c = y intercept
(3) Intercept Form :

x intercept = a
y intercept = b
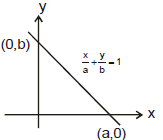
(4) Normal Form :
x cos α + y sin α = p ,where α is the angle which the perpendicular to the line makes with the axis of x and ρ is the length of the perpendicular from the origin to the line. p is always positive
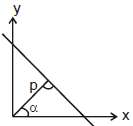
(5) Slope Point Form :
Equation : y - y1 = m (x - x1), is the equation of line passing through the point (x1, y1) and having the slope 'm'
(6) Two points Form :
Equation : y - y1 =  , is the equation of line passing through two points (x1, y1) and (x2, y2)
, is the equation of line passing through two points (x1, y1) and (x2, y2)
(7) Parametric Form :
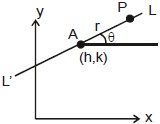
To find the equation of a straight line which passes through a given point A(h, k) and makes a given angle θ with the positive direction of the x-axis. P(x, y) is any point on the line LAL'.
Let AP = r, x - h = r cosθ, y - k = r sinθ
 is the equation of the straight line LAL'.
is the equation of the straight line LAL'.
Any point on the line will be of the form (h + r cosθ, k + r sinθ), where |r| gives the distance of the point P from the fixed point (h, k)
Note : If point P is taken relatively upward to A then r is positive otherwise negative. If line is parallel to x-axis then for he point right to A, r is positive and for left to A, r is negative.
D. Reduction Of General Equation To Different Standard Forms
(1) Slope - Intercept Form :
To reduce the equation Ax + By + C = 0 to the form y = mx + c
Given equation is Ax+ By + C = 0

Note : Slope of the line Ax + By + c = 0 is -A/B i.e. 
(2) Intercept Form :
To reduce the equation Ax + By + C = 0 the form x/a + y/b = 1. This reduction is possible only when C ≠ 0 Given equation is Ax + By = – C


Note : Intercept on the x-axis =  , intercept on the y-axis =
, intercept on the y-axis =  . Thus intercept of a straight line on the x-axis can be obtained by putting y = 0 in the equation of the line and then finding the value of x. similarly, intercept on the y-axis can be obtained by putting x = 0 and solving for y.
. Thus intercept of a straight line on the x-axis can be obtained by putting y = 0 in the equation of the line and then finding the value of x. similarly, intercept on the y-axis can be obtained by putting x = 0 and solving for y.
(3) Normal form :
To reduce the equation Ax + By + C = 0 to the form x cos a + y sin a = p
Given equation is Ax + By + C = 0 or, Ax + By = - C
Case I : When – C > 0, then normal form is 

Case II : When –C < 0, the write the equation as –Ax – By = C


Note : In the normal form 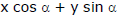 = p, p is always taken as positive.
= p, p is always taken as positive.
Ex.5 Reduce the line 2x - 3y + 5 = 0, in slope intercept, intercept and normal forms.
Sol.
Slope - Intercept Form :




Ex.6 Find the equations of the lines which pass through the point (3, 4) and the sum of their respective intercepts on the axes is 14.
Sol.
Let the equation of the line be x/a + y/b = 1 ....(1)
This passes through (3, 4) therefore 3/a + 4/b ....(2)
It is given that a + b = 14 = b = 14 – a
Putting b = 14 – a in (ii), we get

⇒ (a – 7) (a – 6) = 0 ⇒ a = 7, 6 ⇒ two such lines are there.
For a = 7, b = 14 – 7 = 7 and for a = 6, a = 14 – 6 = 8
Putting the values of a and b in (i), we get the equations of lines
 or x + y = 7 and 4x + 3y = 24.
or x + y = 7 and 4x + 3y = 24.
Ex.7 A rod of steel is fixed at A (4, 0) and a toy is placed on it at B (0, 4). Now rod is rotated about A through an angle of 15° in clockwise direction, then find the new position of a toy.
Sol.
Let new position of a toy be C.


Rod is rotated through 15° in clockwise
θnew = 135° - 15° = 120°
AB = 4√2 ⇒ h = 4, k = 0
Hence C = (h + r cos θ, k = r sin θ) = (4 + 4√2 cos 120°, 0 + 4√2 sin 120°) = (4 – 2√2, 2√2 )
Ex.8 If the straight line through the point P(3, 4) makes an angle π/6 with the x-axis and meets the line 12x + 5y + 10 = 0 at Q, find the length of PQ
Sol. The equation of a line passing through P(3, 4) and making an angle = π/6 with the x-axis is
 where r represents the distance of any point on this line from the given point P(3, 4). The co-ordinates of any point Q on this line are
where r represents the distance of any point on this line from the given point P(3, 4). The co-ordinates of any point Q on this line are 
If Q lies on 12x +15y + 10 = 0, then


Ex.9 A canal is 4 1/2 kms from a place and the shortest route from this place to the cenal is exactly north east. A village is 3 kms north and 4 kms east from the place. Does it lie on canal?
Sol.
Let AB be the canal and O be the given place.
Let L be the foot of perpendicular from O to AB.
Given, OL = 9/2. And ∠AOL = 45°


Let S be the given village, then S = (4, 3). Putting x = 4 and y = 3 in equation (1), we get 4 + 3 = 9/2 which is not true. Thus the co-ordinates of S doesn't satisfy equation (1) and hence the given village does not lie on the canal.
(4) Position of a point w.r. to a line L : Ax + By + c = 0
(i) If the points P(x1 y1( & Q(x2, y2) lies on the same side of the line Ax + By + C = 0 then the expressions Axj + Byj + C & Ax2 + By2 + C have same sign otherwise if P and Q lies on opposite side then Ax1 + By1 + C and Ax2 + By2 + C will have opposite sign.
(ii) If only one point is given then position of that point is checked w.r. to origin
|
75 videos|238 docs|91 tests
|
FAQs on Point Slope Form and Two Point Form - Mathematics (Maths) Class 11 - Commerce
| 1. What is the point-slope form of a linear equation? |  |
| 2. How do I convert a linear equation from point-slope form to slope-intercept form? |  |
| 3. Can I use the point-slope form to find the equation of a line given two points? |  |
| 4. What is the two-point form of a linear equation? |  |
| 5. How do I convert a linear equation from two-point form to slope-intercept form? |  |

|
Explore Courses for Commerce exam
|

|

















