Polarization of Light | Oscillations, Waves & Optics - Physics PDF Download
Plane of Incidence
Incident ray, reflected ray, refracted ray and normal to incidence forms a plane that plane
is plane of incidence.
Plane of Polarization
The plane passing through the direction of propagation and containing no vibration is
called the “Plane of Polarization”.
Production of Plane Polarized Light
Different methods of production of polarized light
- Polarization by reflection
- Polarization by refraction
- Polarization by selective absorption
- Polarization by double refraction
- Polarization by scattering
Polarization by Reflection
If a linearly polarized wave (Electric vector associated with the incident wave lies in the
plane of incidence) is incident on the interface of two dielectrics with the angle of
incidence equal toθ . If the angle of incidence θ is such that
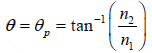
then the reflection coefficient is zero.
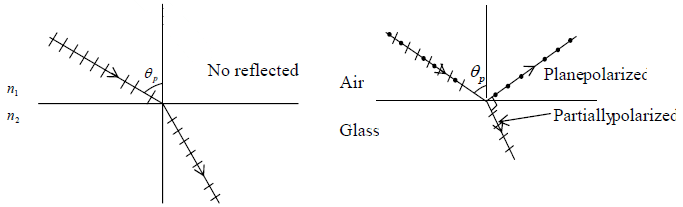
Thus if an unpolarized beam is incident with an angle of incidence equal to p θ , the
reflected beam is plane polarized whose electric vector is perpendicular to the plane of
incidence.
Above equation is known as Brewster’s law. The angle θp is known as the polarizing
angle or the Brewster angle. At this angle, the reflected and the refracted rays are at right
angle to each other i.e.
θp + r = π/2 ⇒ n = 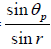 =
= 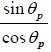 ⇒ tanθp = n
⇒ tanθp = n
For the air-glass interface, n1 =1 and n2 ≈1.5 giving θp ≈ 570
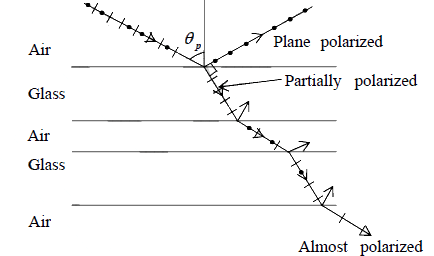
Polarization by Refraction
If an unpolarized beam is incident with an angle of incidence equal to p θ , the reflected
beam is plane polarized whose electric vector is perpendicular to the plane of incidence.
The transmitted beam is partially polarized and if this beam is made to undergo several
reflections, then the emergent beam is almost plane polarized with its electric vector in
the plane of incidence.
If Ip and Is be the intensity of the parallel and perpendicular component in refracted
light, then the degree of polarization is given by
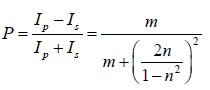
where m is the number of plate and n is the refractive index.
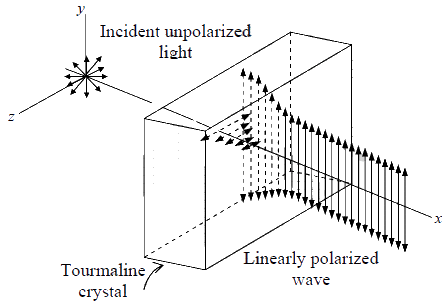
Polarization by selective absorption
A simple method for eliminating one of the beams is through selective absorption; this
property of selective absorption is known as dichroism. A crystal such as tourmaline has
different coefficients of absorption for the two linearly polarized beams into which the
incident beam splits up. Consequently, one of the beams gets absorbed quickly, and the
other component passes through without much attenuation. Thus, if an unpolarized beam
is passed through a tourmaline crystal, the emergent beam will be linearly polarized
Polarization by Double Refraction
When a ray of unpolarized light passed through doubly refracting crystal (calcite or
quartz), it split up into two refracted rays. One of the ray obeys the ordinary laws of
refraction i.e. ( n remains constant) and it is called ‘ordinary ray’ (o -ray). The other
behaves in an extra ordinary way (i.e. n varies) and called ‘extraordinary ray’ ( e -ray).
It is found that both the ordinary and extraordinary rays are plane-polarized having
vibration perpendicular to each other.
If one can sandwich a layer of a material whose refractive index lies between the two,
then for one of the beams, the incidence will be at a rarer medium and for the other it will
be at a denser medium. This 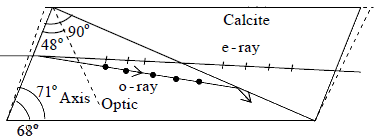
principle is used in a Nicol prism
which consists of a calcite crystal
cut in such a way that for the
beam, for which the sandwiched
material is a rarer medium, the angle of incidence is greater than the critical angle. Thus
this particular beam will be eliminated by total internal reflection. Following figure
shows a properly cut calcite crystal in which a layer of Canada balsam has been
introduced so that the ordinary ray undergoes total internal reflection. The extraordinary
component passes through, and the beam emerging from the crystal is linearly polarized.
Polarization by Scattering
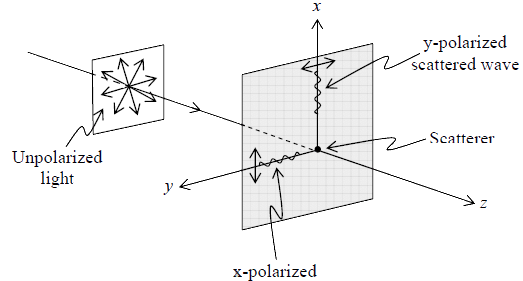
When an unpolarized beam moving in z -axis, strike a gas atom than the electric field in
unpolarized beam sets the electric charges in the gas atom in vibration. Since the E -field
is in xy plane, therefore, the vibration will take place in xy plane only. These vibration
can resolve in x and y direction and can said that two dipoles oscillating one in x and
other in y -direction with the frequency of incident light. Since an oscillating dipole does
not radiate in the direction of its own length.
Therefore, observer along x -axis will receive light component vibrating only in y -
direction and along y -axis the component will vibrate only x axis. Hence observer will
receive Plane Polarized light.
Blue colour of sky
Lord Rayleigh Formula: Intensity of light scattered from firie particles (dimension ≤ λ )
varies inversely as the fourth power of λ . i.e. 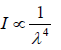 Scattered intensity of blue light is more than red blue red ∵ λblue < λred .
Scattered intensity of blue light is more than red blue red ∵ λblue < λred .
Why blue scattered more: Natural frequency of bound electron in gas lies in ultra-violet region. Blue light closer to natural frequency than red light, therefore, blue is more effective in causing the electron to oscillate and thus it get more effectively scattered than red.
Red colour of sunrise and sunset
The path of the light through the atmosphere at sunrise and sunset is greatest. Since the violet & blue light is largely scattered and get removed and what we see is rest having red component.
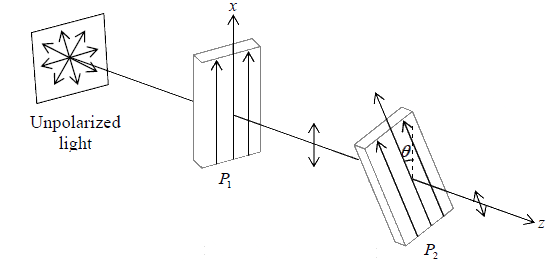
Malus’ law
An unpolarized light beam gets polarized after passing through the Polaroid P1 which has a pass axis parallel to the x axis. When this x -polarized light beam incident on the second Polaroid P2 whose pass axis makes an angle θ with the x axis, than the intensity of the emerging beam will vary as I = I0 cos2θ where I0 represents the intensity of the emergent beam when the pass axis of P2 is also along the x axis (i.e., when θ = 0 ), above equation known as Malus’ law.
Thus, if a linearly polarized beam is incident on a Polaroid and if the Polaroid is rotated about the z axis, then the intensity of the emergent wave will vary according to the above law.
|
54 videos|22 docs|14 tests
|
FAQs on Polarization of Light - Oscillations, Waves & Optics - Physics
| 1. What is the plane of incidence in the context of polarization of light? |  |
| 2. How does refraction affect the polarization of light? |  |
| 3. What is Malus' law and how is it related to polarization of light? |  |
| 4. How is the polarization of light relevant to IIT JAM exam? |  |
| 5. Can you provide an example of how the plane of incidence affects the polarization of light? |  |