Polarization of light - I: Assignment | Oscillations, Waves & Optics - Physics PDF Download
Q.1. Two polarizing sheets have their polarizing directions parallel. Determine the angle by which either sheet must be turned so that the intensity falls to half of its value.
Iθ = Imaxcos2θ (Malus’ Law)
cosθ =
θ = ±45 , ± 135
Q.2. Light is incident from water (μ =1.33) on the glass (μ =1.5) . Find the polarizing angle for the boundary separating water and glass.
= 1.1278
∴QP = 48.4o
Q.3. A system of three polarizing sheets intercept a beam of initially unpolarized light. The polarizing direction of the first sheet is parallel the y - axis that of the second sheet is at angle of θ counterclockwise from the y - axis and that of the third sheet is parallel to the x -axis. The intensity of light emerging from the three-sheet system is 11.52% of the original intensity I0 . Determine to angle θ . In which direction is the emerging light polarized.
As the light passing through the first sheet is unpolarized, the intensity I1 of the light transmitted by the first sheet is given by the one-half rule:
Because the polarizing direction of the first sheet is parallel to the y - axis, the polarization of the light transmitted by it is also along y - axis.
Because the light reaching the second sheet is polarized, the intensity I 2 of the light transmitted by that sheet is given by the cosine-squared rule. The angle q in the rule is the angle between the polarization direction of the incoming light, parallel to the y - axis, and the polarizing direction of the second sheet, q being counterclockwise from the y -
axis. Thus
Because the light entering the third sheet is polarized and the polarizing between the second and the third sheets is ( 90 -θ ) , the transmitted intensity is again given by Malus law. Thus
From (iii), (ii) and (i)
or
cos4θ - cos2θ + 0.2304 = 0
cos2θ = 0.64 or 0.36
cosθ = ±0.8 or ±0.6
θ = 36.870 or 53.130
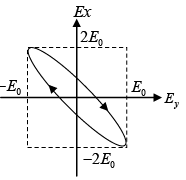
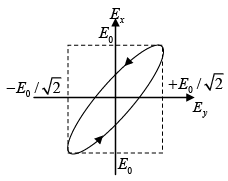
Q.4. The electric field components of a plane electromagnetic wave are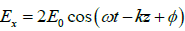 ;
; 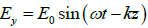 . Draw the diagram showing the state of
. Draw the diagram showing the state of
polarization ( i.e . Circular, plane, elliptical or unpolarized) when
(a) ∅ = 0 (b) ∅ =π / 2 (c) ∅ =π / 4
and
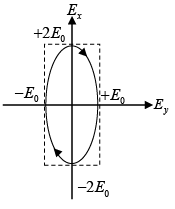
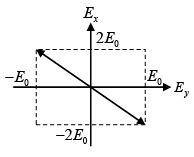
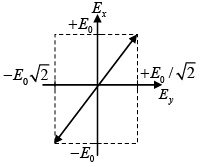
(a) At ∅ = 0 ,
=

The phase difference is δ = π/2 and amplitudes are not equal.
Therefore, it represent elliptically polarized.
Since at z = 0 ,
It is a right elliptically polarized
(b) At ∅ = π/2
The phase difference is δ = 0 , therefore it represents linearly polarized.
Since at z = 0 ,
(c) At ∅ =π / 4
The phase difference is δ = 3π/4 and amplitudes are not equal. Therefore, it represents
elliptically polarized
Since, at z = 0 ,
,
It is right elliptically polarized.
Q.5. What will be the Brewster angle for a glass slab (n =1.5) immersed in water (n = 4/3).
=
=
= 48.40
Q.6. The value of refractive indices for ordinary and extraordinary rays no and ne for calcite are 1.642 and 1.478, respectively. Calculate the phase retardation for λ= 6000Ao with the plate thickness 0.04mm.
Path difference introduced by the plate
Δx= (no - ne)t = (1.642- 1.478) x 4 x 10-5 = 6.56 x 10-6m
Phase difference
δ =
= 68.66 rad
Q.7. Sun rays incident obliquely on a pond are completely polarized by reflection. Find the elevation of the sun (in degrees) above the horizon.
tanθp = μ = 1.33 (Brewster’s law)
∴θp = 530
Therefore, the elevation of the sun is 90 - 530 = 370
Q.8. What is the minimum thickness of a quarter wave plate if the material has μ =1.553 and μe = 1.544 at a wavelength of λ = 6000Ao.
t =
=
= 1.67 x 10-3 cm
Q.9. Discuss the state of polarization when the x and y components of the electric field are given by the following equations:
(a) 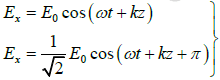
(b) 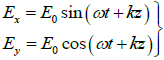
(c) 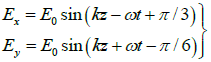
(d) 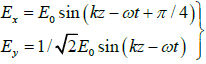
(a)
At z = 0 ,
The phase difference is δ =π . Therefore, it is linearly polarized.
(b)
,
At z = 0 ,
The phase difference is δ = π/2 and amplitudes are equal, therefore it represents the
circularly polarized light.
It is a left circularly polarized.
(c)
At z = 0 ,
The phase difference is δ = π/2 and amplitudes are equal. Therefore, it represents circularly polarized light.
Since,
It is a right circularly polarized
(d)
At z = 0 ;
The phase difference is δ = π/4 , therefore, it represents elliptically polarized light It is a left elliptically polarized
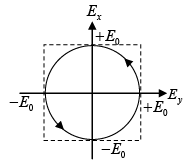
Q.10. A right – circularly polarized beam is incident on a calcite half - wave plate. Show that the emergent beam will be left – circularly polarized.
Equation of right circularly polarized beam is
Calcite half wave plate introduced additional π phase difference. Thus, the equation of emergent beam is
and Ey = E0sin(ωt)
which represents left circularly polarized beam.
|
54 videos|22 docs|14 tests
|
FAQs on Polarization of light - I: Assignment - Oscillations, Waves & Optics - Physics
| 1. What is polarization of light? |  |
| 2. How is light polarized? |  |
| 3. What are some applications of polarized light? |  |
| 4. How does polarization affect the intensity of light? |  |
| 5. Can all types of light be polarized? |  |

|
Explore Courses for Physics exam
|

|
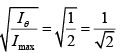
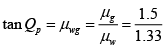 = 1.1278
= 1.1278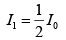

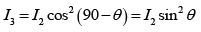
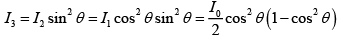
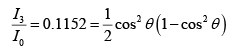
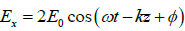 and
and 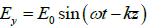
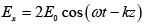 =
= 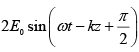
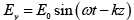
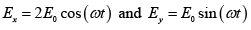
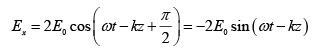

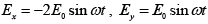
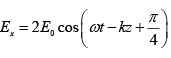
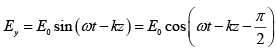
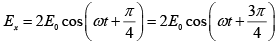 ,
, 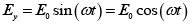
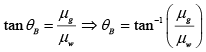 =
= 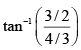 =
= 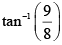 = 48.40
= 48.40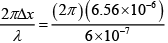 = 68.66 rad
= 68.66 rad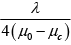 =
= 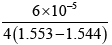 = 1.67 x 10-3 cm
= 1.67 x 10-3 cm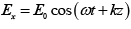
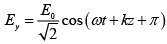
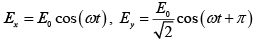
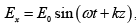 ,
,
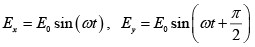
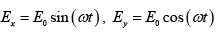
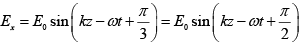
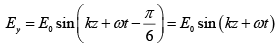
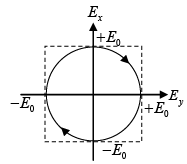
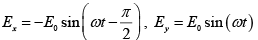
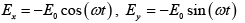
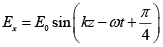

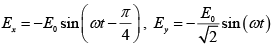
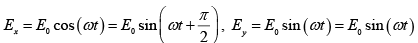
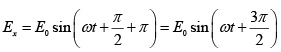 and Ey = E0sin(ωt)
and Ey = E0sin(ωt)
















