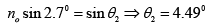Polarization of light - II: Assignment | Oscillations, Waves & Optics - Physics PDF Download
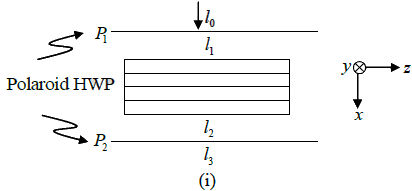
Q.1. A HWP (half-wave plate) is introduced between two crossed Polaroids P1 and P2. The optics axis makes an angle 15o with the pass axis of P1 as shown in figure (i) and (ii) given below. If an unpolarized beam of intensity I0 is normally incident on P1 and if I1,I2 and I3 are the intensities after P1 , after HWP and after P2 respectively then calculate I1/I0/I2/I0 and I3 / I0 .
(a)
(b)
(c)
where θ is the angle between optic axis and pass axis P1 and δ is the phase difference between O - ray and e - ray at the exit of Half wave plate.
For half wave plate ( HWP ) ,δ =π
∴
Given θ = 150
∴
⇒
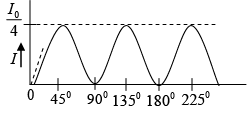
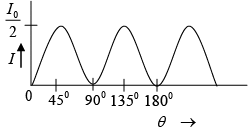
Q.2. A quarter - wave plate is rotated between two crossed polaroids. If a polarized beam is incident on the first Polaroid, discuss the variation of intensity of the emergent beam as the quarter - wave plate is rotated. What will happen if we have a half - wave instead of a quarter - wave plate?
The intensity of light at the exit of Polaroid P2 is

(a) For QWP : δ =π / 2
∴
(b) For HWP : δ =π
∴
Q.3. Consider a calcite HWP whose optic axis is along the y - axis, obtain the output state of polarization when the incident beam is
(a) x - polarized
(b) y - polarized
(c) Left Circularly Polarized (LCP)
(d) Linearly Polarized with its E making an angle of 45o with the y - axis
(e) Linearly Polarized with its E making an angle of 600 with the x - axis
(f) Left Elliptically Polarized (LEP) with its E given by
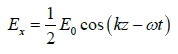
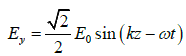
(a)
(b)
(c)
(d)
(e)
(f)
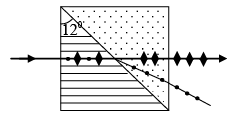
Q.4. Two prisms of calcite ( no > ne ) are cemented together as shown in the figure given below so as to form a cube. Lines and dots show the direction of the optic axis. A beam of unpolarized light is incident normally from region I. Assume the angle of the prism to be 12o. Determine the path of rays in region II, III and IV indicating the direction of vibrations (i.e. the direction of D).
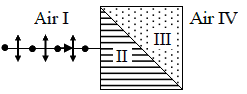
It is example of Rochon Prism. In the first prism both the beams will see the same refractive index n . In second crystal, the o - ray will see the same refractive index and go undeviated. The e - ray will see refractive index ne and will bend away from the normal. The angle of refraction will be determined from the following equation:

Thus, sinr =
sin r = 0.232 ⇒ r ≅13.40
Therefore, the angle of incidence at the second surface will be 13.40 -120= 1.40
The emerging angle will be sinθ = nesin(1.4) ⇒θ ≅ 2.10
Q.5. For calcite the values of n0 and ne for λ0 = 4046A`0 are 1.68134 and 1.49694 respectively; corresponding to λ0 = 7065A0 the values are 1.65207 and 1.48359, respectively. We have a calcite quarter – wave plate corresponding to λ0 = 4046A0. A left – circularly polarized beam of λ0 = 7065A0 is incident on this plate. Obtain the state of polarization of the emergent beam.
Thickness of the calcite plate is
d =
= 5485 x 10-7mm
For λ0 = 7065A0
δ =
=
Equation of left circularly polarized beams
After passing through calcite crystal of thickness d , additional phase difference of π/4 is
introduced between Ex and Ey
∴
It represents the left elliptically polarized beam.
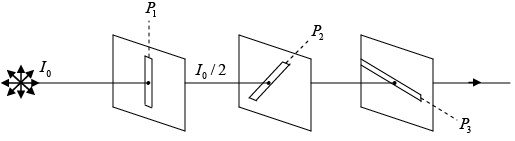
Q.6. (a) Consider two crossed polaroids placed in the path of placed in the path of an unpolarized beam of intensity I0 (see figure). If we place a third polariod in between the two then, in general, some light will be transmitted through. Explain this phenomenon.
(b) Assuming the pass axis of the third polaroid to be at 0 45 to the pass axis of either of the polaroids, calculate the intensity of the transmitted beam. Assume that the polaroids are perfect.
(a)
Let angle between pass axis P1 and P2 is θ the intensity at the exit of P2 is
Since angle between P1 and P3 is 900 Therefore angle between P2 and P3 is 900 -θ
∴ Intensity at the exit of P3 is
=
=
(b) θ = 450
∴
Q.7. In question 3, if the optic axis of the quarter-wave plate makes an angle of 450 with the pass axis of either Polaroid, show that only a quarter of the incident intensity will be transmitted. If the quarter – wave plate is replaced by a half - wave plate is replaced by a half - wave plate, show that half of the incident intensity will be transmitted through.
(a) For QWP : θ =π /2
∴
For θ = 450 :
(b) for HWP : δ =π
∴
For θ = 450 :
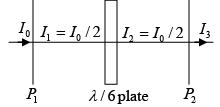
Q.8. A λ/6 plate is introduced in between the two crossed polarization in such a way that the optic axis of the λ/6 plate makes an angle of 450 with the pass axis of the first polarizer (figure given below). Consider an unpolarized beam of intensity I0 to be incident normally on the polarizer. Assume the optic axis to be along the z - axis and the propagation along the x - axis. Write the y and z components of the electric fields (and the corresponding total intensities) after passing through (i) P1 (ii) λ/6 plate and (iii) P2 .
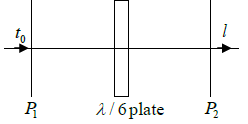
(i) Intensity after P1- is
(ii) Intensity after P2 is
(iii) Intensity after P3 is
where θ is the angle between optic axis and pass axis of P1 and δ is the phase difference between O - ray and e - ray introduced by λ/6- plate.
Given θ =
∴
Q.9. Consider a Wollaston prism consisting of two similar prisms of calcite ( no = 1.66 and ne = 1.49) with angle of prism 250. Calculate the angular divergence of the two emerging beams.
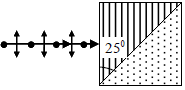
For z - polarized beam: The beam will propagate as an o - ray in first prism with refractive index no = 1.66 . When this beam enters the second prism it will become an e - ray with ne = 1.49
∴
≌ 250
Thus the angle of incident at the second surface will be
i1 = 28- 25= 30
The output angle θ1 will be given by
For y - polarized beam: The beam will propagate as e - ray in the first prism and as an o - ray in the second prism.
The angle of refraction will now be given by
= 22.30
Thus, the angle of incident at the second surface will bei2 = 250 - 22.30 = 2.70
The output angle θ2 will be given by
∴ Angular divergence is θ = θ1 + θ2≌90
|
54 videos|22 docs|14 tests
|
FAQs on Polarization of light - II: Assignment - Oscillations, Waves & Optics - Physics
| 1. What is polarization of light? |  |
| 2. How does polarization of light occur? |  |
| 3. What are the applications of polarized light? |  |
| 4. How does polarized light affect vision? |  |
| 5. Can all types of light be polarized? |  |

|
Explore Courses for Physics exam
|

|
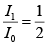
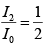
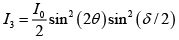
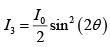
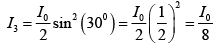

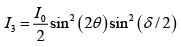
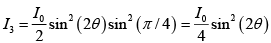
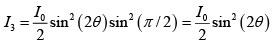


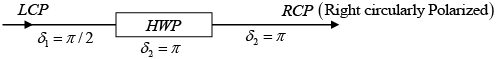
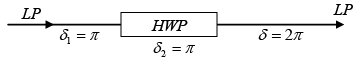
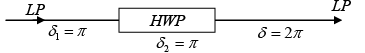
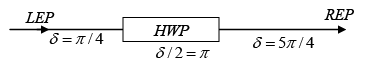
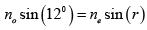
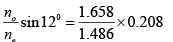
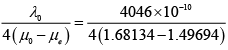 = 5485 x 10-7mm
= 5485 x 10-7mm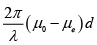 =
= 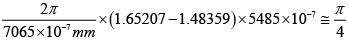
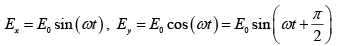
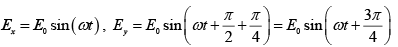
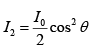
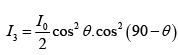 =
= 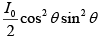 =
= 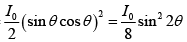
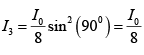
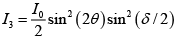
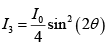
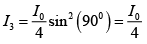

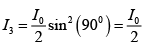
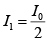

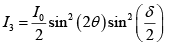
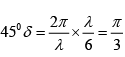
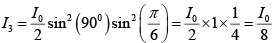
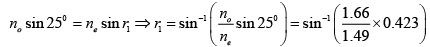 ≌ 250
≌ 250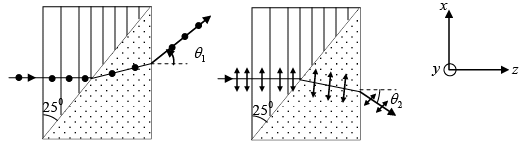
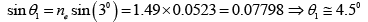
 = 22.30
= 22.30