Postulates & Operators in Quantum Mechanics | Physical Chemistry PDF Download
Postulates of Quantum Mechanics
Here are the Six Postulates of Quantum Mechanics. Postulate 2 contains various Operators use in Quantum Mechanics.
Postulate 1. The state of a quantum mechanical system is completely specified by a function ψ(r, t) that depends on the coordinates of the particle(s) and on time. This function, called the wave function or state function, has the important property that ψ(r, t) ψ(r, t) dτ is the probability that the particle lies in the volume element dτ located at r at time t .
The wavefunction must satisfy certain mathematical conditions because of this probabilistic interpretation. For the case of a single particle, the probability of finding it somewhere is 1, so that we have the normalization condition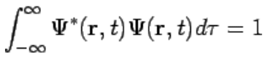 (110)
(110)
It is customary to also normalize many-particle wavefunctions to 1.2 The wavefunction must also be single-valued, continuous, and finite.
Postulate 2. To every observable in classical mechanics there corresponds a linear, Hermitian operator in quantum mechanics.
This postulate comes about because of the considerations raised in section 3.1.5: if we require that the expectation value of an operator  is real, then  must be a Hermitian operator. Some common operators occuring in quantum mechanics are collected in Table 1.
Table 1: Physical observables and their corresponding quantum operators (single particle)
Postulate 3. In any measurement of the observable associated with operator Â, the only values that will ever be observed are the eigenvalues a, which satisfy the eigenvalue equation
ÂΨ = aΨ (111)
This postulate captures the central point of quantum mechanics--the values of dynamical variables can be quantized (although it is still possible to have a continuum of eigenvalues in the case of unbound states). If the system is in an eigenstate of  with eigenvalue a, then any measurement of the quantity A will yield a.
Although measurements must always yield an eigenvalue, the state does not have to be an eigenstate of  initially. An arbitrary state can be expanded in the complete set of eigenvectors of  (ÂΨi = aiΨi) as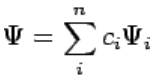 (112)
(112)
where n may go to infinity. In this case we only know that the measurement of A will yield one of the values ai, but we don't know which one. However, we do know the probability that eigenvalue ai will occur--it is the absolute value squared of the coefficient, |ci|2 (cf. section 3.1.4), leading to the fourth postulate below.
An important second half of the third postulate is that, after measurement of Ψ yields some eigenvalue ai, the wavefunction immediately ``collapses'' into the corresponding eigenstate Ψi (in the case that ai is degenerate, then Ψ becomes the projection of Ψ onto the degenerate subspace). Thus, measurement affects the state of the system. This fact is used in many elaborate experimental tests of quantum mechanics.
Postulate 4. If a system is in a state described by a normalized wave function Ψ, then the average value of the observable corresponding to  is given by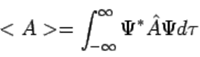 (113)
(113)
Postulate 5. The wavefunction or state function of a system evolves in time according to the time-dependent Schrödinger equation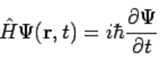 (114)
(114)
The central equation of quantum mechanics must be accepted as a postulate, as discussed in section 2.2.
Postulate 6. The total wavefunction must be antisymmetric with respect to the interchange of all coordinates of one fermion with those of another. Electronic spin must be included in this set of coordinates.
|
90 videos|144 docs|67 tests
|
FAQs on Postulates & Operators in Quantum Mechanics - Physical Chemistry
| 1. What are the postulates of quantum mechanics? |  |
| 2. What is the wavefunction postulate in quantum mechanics? |  |
| 3. How does the measurement postulate work in quantum mechanics? |  |
| 4. What does the time evolution postulate say in quantum mechanics? |  |
| 5. What are operators in quantum mechanics? |  |
















