Practice Doc: CAT 2019 For Quant (Slot - 2) | Additional Study Material for CAT PDF Download
Q.1. The average of 30 integers is 5. Among these 30 integers, there are exactly 20 which do not exceed 5. What is the highest possible value of the average of these 20 integers?
(A) 3.5
(B) 5
(C) 4.5
(D) 4
Ans. (C)
Solution: It is given that the average of the 30 integers = 5
Sum of the 30 integers = 30*5 = 150
There are exactly 20 integers whose value is less than 5.
To maximise the average of the 20 integers, we have to assign minimum value to each of the remaining 10 integers
So the sum of 10 integers = 10*6 = 60
The sum of the 20 integers = 150-60 = 90
Average of 20 integers = 90/20 = 4.5
Q.2. Amal invests Rs 12000 at 8% interest, compounded annually, and Rs 10000 at 6% interest, compounded semi-annually, both investments being for one year. Bimal invests his money at 7.5% simple interest for one year. If Amal and Bimal get the same amount of interest, then the amount, in Rupees, invested by Bimal is
Ans. 20920
Solution: The amount with Amal at the end of 1 year = 12000*1.08+10000*1.03*1.03 = 23569
Interest received by Amal = 23569 -22000 =1569
Let the amount invested by Bimal = 100b
Interest received by Bimal = 100b*7.5*1/100 = 7.5b
It is given that the amount of interest received by both of them is the same 7.5b = 1569
b = 209.2
Amount invested by Bimal = 100b = 20920
Q.3. What is the largest positive integer n such that 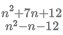 is also a positive integer?
is also a positive integer?
(A) 6
(B) 16
(C) 8
(D) 12
Ans. (D)
Solution:
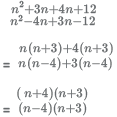
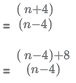
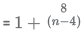
which will be maximum when n - 4 = 8
n = 12 D is the correct answer.
Q.4. How many pairs (m, n) of positive integers satisfy the equation m2 + 105 = n2?
Ans. 4
Solution:
n2 − m2 = 105
(n - m)(n + m) = 1*105, 3*35, 5*21, 7*15, 15*7, 21*5, 35*3, 105*1.
n - m = 1, n + m = 105 ⇒ n = 53, m = 52
n - m = 3, n + m = 35 ⇒ n = 19, m = 16
n - m = 5, n + m = 21 ⇒ n = 13, m = 8
n - m = 7, n + m = 15 ⇒ n = 11, m = 4
n - m = 15, n + m = 7 ⇒ n = 11, m = -4
n - m = 21, n + m = 5 ⇒ n = 13, m = -8
n - m = 35, n + m = 3 ⇒ n = 19, m = -16
n - m = 105, n + m = 1 ⇒ n = 53, m = -52
Since only positive integer values of m and n are required. There are 4 possible solutions.
Q.5. Two ants A and B start from a point P on a circle at the same time, with A moving clock-wise and B moving anti-clockwise. They meet for the first time at 10:00 am when A has covered 60% of the track. If A returns to P at 10:12 am, then B returns to P at
(A) 10:25 am
(B) 10:45 am
(C) 10:18 am
(D) 10:27 am
Ans. (D)
Solution:
When A and B met for the first time at 10:00 AM, A covered 60% of the track.
So B must have covered 40% of the track.
It is given that A returns to P at 10:12 AM i.e A covers 40% of the track in 12 minutes
60% of the track in 18 minutes
B covers 40% of track when A covers 60% of the track.
B covers 40% of the track in 18 minutes.
B will cover the rest 60% in 27 minutes, hence it will return to B at 10:27 AM
Q.6. Let a1, a2,..be integers such that
a1 − a2 + a3 − a4 + .... + (−1)n−1an = n, n ≥ 1.
Then a51 + a52 + .... + a1023 equals
(A) 0
(B) 1
(C) 10
(D) -1
Ans. (B)
Solution:
a1 − a2 + a3 − a4 + .... + (−1)n−1an = n
It is clear from the above equation that when n is odd, the co-efficient of a is positive otherwise negative.
a1 − a2 = 2
a1 = a2 + 2
a1 − a2 + a3 = 3
On substituting the value of in the above equation, we get
a3 = 1
a1 − a2 + a3 − a4 = 4
On substituting the values of a1, a3 in the above equation, we get
a4 = -1
a1 − a2 + a3 − a4 + a5 = 5
On substituting the values of in the above equation, we get
a5 = 1
So we can conclude that a3, a5, a7...an + 1 and a2, a4, a6...a2n = -1
Now we have to find the value of a51 + a52 + .... + a1023
Number of terms = 1023 = 51+(n-1)1
n = 973
There will be 486 even and 487 odd terms, so the value of a51 + a52 + .... + a1023 = 486*-1+487*1 = 1
Q.7. Two circles, each of radius 4 cm, touch externally. Each of these two circles is touched externally by a third circle. If these three circles have a common tangent, then the radius of the third circle, in cm, is
(A) 1/√2
(B) π/3
(C) √2
(D) 1
Ans. (D)
Solution:
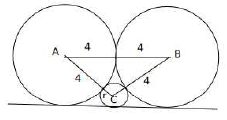
Let 'h' be the height of the triangle ABC, semiperimeter(S)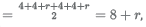
a = 4 + r, b = 4 + r, c = 8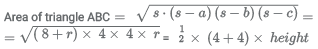
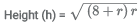
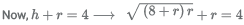
(Considering the height of the triangle)
16r = 16
r = 1
Alternatively,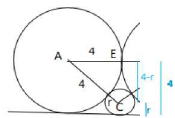
AE@ + EC2 = AC2 ⟶ 42 + (4 − r)2 = (4 + r)2 ⟶ ⟶ ⟶ r = 1
Q.8. Let A be a real number. Then the roots of the equation x2 - 4x - log2A = 0 are real and distinct if and only if
(A) 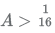
(B) 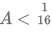
(C) 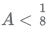
(D) 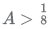
Ans. (A)
Solution:
The roots of x2 - 4x - log2A = 0 will be real and distinct if and only if the discriminant is greater than zero 1
6 + 4*log2A > 0
log2A > -4
A > 1/16
Q.9. The quadratic equation x2 + bx + c = 0 has two roots 4a and 3a, where a is an integer. Which of the following is a possible value of b2 + c?
(A) 3721
(B) 361
(C) 427
(D) 549
Ans. D
Solution:
Given,
The quadratic equation x2 + bx + c = 0 has two roots 4a and 3a
7a = -b
12a2 = c
We have to find the value of b2 + c = 49a2 + 12a2 = 61a2
Now lets verify the options
61a2 = 3721 ⇒ a = 7.8 which is not an integer
61a2 = 361 ⇒ a = 2.42 which is not an integer
61a2 = 427 ⇒ a = 2.64 which is not an integer
61a2 = 3721 ⇒ a = 3 which is an integer
Q.10. The base of a regular pyramid is a square and each of the other four sides is an equilateral triangle, length of each side being 20 cm.
The vertical height of the pyramid, in cm, is
(A) 12
(B) 10√2
(C) 8√3
(D) 5√5
Ans. (B)
Solution: It is given that the base of the pyramid is square and each of the four sides are equilateral triangles.
Length of each side of the equilateral triangle = 20cm
Since the side of the triangle will be common to the square as well, the side of the square = 20cm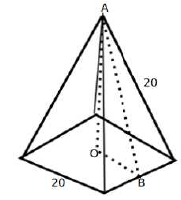
Let h be the vertical height of the pyramid ie OA
OB = 10 since it is half the side of the square
AB is the height of the equilateral triangle i.e 10√3
AOB is a right angle, so applying the Pythagorean formula, we get
OA2 + OB2 = AB2
h2 + 100 = 300
h = 10√2
Q.11. Let ABC be a right-angled triangle with hypotenuse BC of length 20 cm. If AP is perpendicular on BC, then the maximum possible length of AP, in cm, is
(A) 10
(B) 5
(C) 8√2
(D) 6√2
Ans. (A)
Solution: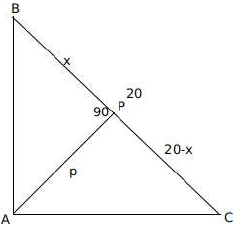
Let p be the length of AP.
It is given that ∠BAC = 90 and ∠APC = 90
Let ∠ABC, = θ, then ∠BAP = 90 - θ and ∠BCA = 90 - θ
So ∠PAC = θ
Triangles BPA and APC are similar
p2 = x (20 -x)
We have to maximize the value of p, which will be maximum when x = 20 - x
x = 10
Q.12. If x is a real number, then 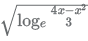 is a real number if and only if
is a real number if and only if
(A) 1 ≤ x ≤ 3
(B) 1 ≤ x ≤ 2
(C) −1 ≤ x ≤ 3
(D) −3 ≤ x ≤ 3
Ans. (A)
Solution:

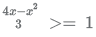
4x − x2 − 3 > = 0
x2 − 4x + 3 = < 0
1= < x = < 3
Q.13. 5x − 3y = 13438 and 5x−1 + 3y+1 = 9686, then x + y equals
Ans. 13
Solution:
5x − 3y = 13438 5x−1 + 3y+1 = 9686
5x + 3y ∗ 15 = 9686 ∗ 5
5x + 3y ∗ 15 = 48430
16*3y = 34992
3y = 2187
y = 7
5x = 13438 + 2187 = 15625
x = 6
x + y = 13
Q.Q.14. The strength of a salt solution is p% if 100 ml of the solution contains p grams of salt. Each of three vessels A, B, C contains 500 ml of salt solution of strengths 10%, 22%, and 32%, respectively. Now, 100 ml of the solution in vessel A is transferred to vessel B. Then, 100 ml of the solution in vessel B is transferred to vessel C. Finally, 100 ml of the solution in vessel C is transferred to vessel A. The strength, in percentage, of the resulting solution in vessel A is
(A) 15
(B) 13
(C) 12
(D) 14
Ans. (D)
Solution:
Each of three vessels A, B, C contains 500 ml of salt solution of strengths 10%, 22%, and 32%, respectively.
The amount of salt in vessels A, B, C = 50 ml, 110 ml, 160 ml respectively.
The amount of water in vessels A, B, C = 450 ml, 390 ml, 340 ml respectively.
In 100 ml solution in vessel A, there will be 10ml of salt and 90 ml of water Now, 100 ml of the solution in vessel A is transferred to vessel B. Then, 100 ml of the solution in vessel B is transferred to vessel C.
Finally, 100 ml of the solution in vessel C is transferred to vessel A i.e after the first transfer, the amount of salt in vessels A, B, C = 40, 120, 160 ml respectively.
After the second transfer, the amount of salt in vessels A, B, C =40, 100, 180 ml respectively.
After the third transfer, the amount of salt in vessels A, B, C = 70, 100, 150 respectively.
Each transfer can be captured through the following table.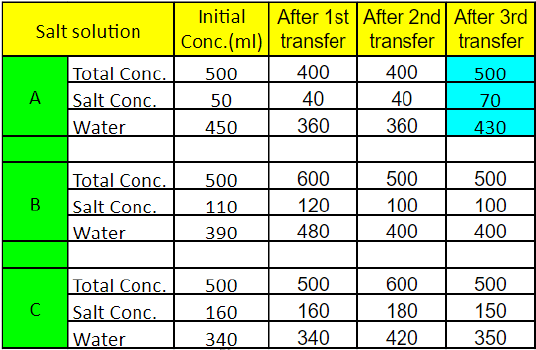
Percentage of salt in vessel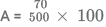
= 14%
Q.15. A cyclist leaves A at 10 am and reaches B at 11 am. Starting from 10:01 am, every minute a motorcycle leaves A and moves towards B.
Forty-five such motorcycles reach B by 11 am. All motorcycles have the same speed. If the cyclist had doubled his speed, how many motorcycles would have reached B by the time the cyclist reached B?
(A) 22
(B) 23
(C) 15
(D) 20
Ans. (C)
Solution:
It is given that starting from 10:01 am, every minute a motorcycle leaves A and moves towards B.
Forty-five such motorcycles reach B by 11 am.
It means that the forty-fifth motorcycle starts at 10:45 AM at A and reaches B by 11:00 AM i.e 15 minutes.
Since the speed of all the motorcycles is the same, all the motorcycles will take the same duration i.e 15 minutes.
If the cyclist doubles the speed, then he will reach B by 10:30 AM. (Since if the speed is doubled, time is reduced by half) Since each motorcycle takes 15 minutes to reach B, 15 motorcycles would have reached B by the time the cyclist reaches B
Q.16. A man makes complete use of 405 cc of iron, 783 cc of aluminium, and 351 cc of copper to make a number of solid right circular cylinders of each type of metal. These cylinders have the same volume and each of these has radius 3 cm. If the total number of cylinders is to be kept at a minimum, then the total surface area of all these cylinders, in sq cm, is
(A) 1026(1 + π)
(B) 8464π
(C) 928π
(D) 1044(4 + π)
Ans. (A)
Solution:
It is given that the volume of all the cylinders is the same, so the volume of each cylinder = HCF of (405, 783, 351)
= 27
The number of iron cylinders = 405/27 = 15
The number of aluminium cylinders = 783/27 = 29
The number of copper cylinders = 351/27 = 13
15*πr2h = 405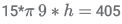
π h = 3
Now we have to calculate the total surface area of all the cylinders
Total number of cylinders = 15 + 29 + 13 = 57
Total surface area of the cylinder = 57*(2π rh + 2π r2)
= 57(2*3*3 + 2*9*π)
= 1026(1 + π)
Q.17. The real root of the equation is 26x + 23x+2 - 21 = 0 is
(A) log2 9
(B)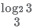
(C) log2 27
(D)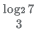
Ans. (B)
Solution:
Let = v
26x + 23x+2 − 21 = 0
= v2 + 4v − 21 = 0
= (v + 7)(v - 3) = 0
v = 3, -7
23x = 3 or 23x = -7(This can be negated)
3x = log2 3
x = log2 3/3
Q.18. How many factors of 24 × 35 × 104 are perfect squares which are greater than 1?
Ans. 44
Solution:
24 × 35 × 104
= 24 × 35 × 24 ∗ 54
= 28 × 35 × 54
For the factor to be a perfect square, the factor should be even power of the number.
In 28, the factors which are perfect squares are 20, 22, 24, 26, 28, = 5
Similarly, in 35, the factors which are perfect squares are 30, 32, 34 = 3
In 54, the factors which are perfect squares are 50, 52, 54 = 3
Number of perfect squares greater than 1 = 5*3*3-1
= 44
Q.19. In a six-digit number, the sixth, that is, the rightmost, digit is the sum of the first three digits, the fifth digit is the sum of first two digits, the third digit is equal to the first digit, the second digit is twice the first digit and the fourth digit is the sum of fifth and sixth digits.
Then, the largest possible value of the fourth digit is
Ans. 7
Solution:
Let the six-digit number be ABCDEF
F = A + B + C, E = A + B, C = A, B = 2A, D = E + F.
Therefore D = 2A + 2B + C = 2A + 4A + A = 7A.
A cannot be 0 as the number is a 6 digit number.
A cannot be 2 as D would become 2 digit number.
Therefore A is 1 and D is 7.
Q.20. John jogs on track A at 6 kmph and Mary jogs on track B at 7.5 kmph. The total length of tracks A and B is 325 metres. While John makes 9 rounds of track A, Mary makes 5 rounds of track B. In how many seconds will Mary make one round of track A?
Ans. 48
Solution:
Speed of John = 6kmph
Speed of Mary = 7.5 kmph
Lengths of tracks A and B = 325 m
Let the length of track A be a, then the length of track B = 325-a
9 rounds of John on track A = 5 rounds of Mary on track B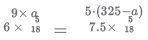
On solving we get , 13a = 1300
a = 100
The length of track A = 100m, track B = 225m
Mary makes one round of track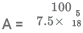
= 48 sec
Q.21. In 2010, a library contained a total of 11500 books in two categories - fiction and nonfiction. In 2015, the library contained a total of 12760 books in these two categories. During this period, there was 10% increase in the fiction category while there was 12% increase in the non-fiction category. How many fiction books were in the library in 2015?
(A) 6160
(B) 6600
(C) 6000
(D) 5500
Ans. (B)
Solution:
Let the number of fiction and non-fiction books in 2010 = 100a, 100b respectively
It is given that the total number of books in 2010 = 11500
100a + 100b = 11500 .......Eq 1
The number of fiction and non-fiction books in 2015 = 110a, 112b respectively
110a + 112b = 12760 .......Eq 2
On solving both the equations we get, b = 55, a = 60
The number of fiction books in 2015 = 110*60=6600
Q.22. John gets Rs 57 per hour of regular work and Rs 114 per hour of overtime work. He works altogether 172 hours and his income from overtime hours is 15% of his income from regular hours. Then, for how many hours did he work overtime?
Ans. 12
Solution: It is given that John works altogether 172 hours i.e including regular and overtime hours.
Let a be the regular hours, 172-a will be the overtime hours
John's income from regular hours = 57*a
John's income for working overtime hours = (172-a)*144
It is given that his income from overtime hours is 15% of his income from regular hours
a*57*0.15 = (172-a)*114
a = 160
The number of hours for which he worked overtime = 172 - 160 = 12 hrs
Q.23. If (2n + 1) + (2n + 3) + (2n + 5) + ... + (2n + 47) = 5280, then whatis the value of 1 + 2 + 3 + .. + n?
Ans. 4851
Solution:
Let us first find the number of terms
47 = 1+(n-1)2
n = 24
24*2n+1+3+5+....47 = 5280
48n + 576 = 5280
48n = 4704 n = 98
Sum of first 98 terms = 98*99/2
= 4851
Q.24. A shopkeeper sells two tables, each procured at cost price p, to Amal and Asim at a profit of 20% and at a loss of 20%, respectively.
Amal sells his table to Bimal at a profit of 30%, while Asim sells his table to Barun at a loss of 30%. If the amounts paid by Bimal and Barun are x and y, respectively, then (x − y) / p equals
(A) 1
(B) 1.2
(C) 0.50
(D) 0.7
Ans. (A)
Solution:
CP of the table at which the shopkeeper procured each table = p
It is given that shopkeeper sold the tables to Amal and Asim at a profit of 20% and at a loss of 20%, respectively
The selling price of the tables = 1.2p and 0.8p to Amal and Asim respectively.
Amal sells his table to Bimal at a profit of 30%
So, CP of the table by Bimal (x)= 1.2p*1.3 = 1.56p
Asim sells his table to Barun at a loss of 30%
So, CP of the table by Barun (y)= 0.7*0.8p = 0.56p
(x-y)/p = (1.56p-0.56p)/p = p/p = 1
Q.25. In a triangle ABC, medians AD and BE are perpendicular to each other, and have lengths 12 cm and 9 cm, respectively. Then, the area of triangle ABC, in sq cm, is
(A) 78
(B) 80
(C) 72
(D) 68
Ans. (C)
Solution:
It is given that AD and BE are medians which are perpendicular to each other.
The lengths of AD and BE are 12cm and 9cm respectively.
It is known that the centroid G divides the median in the ratio of 2:1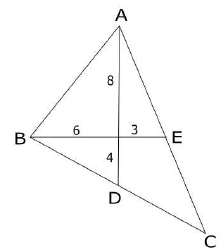
Area of Δ ABC = 2* Area of the triangle ABD
Area of Δ ABD = Area of Δ AGB + Area of Δ BGD
Since ∠ AGB = ∠ BGD = 90 (Given)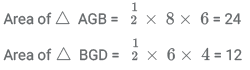
Area of Δ ABD = 24 + 12 = 36
Area of Δ ABC = 2 × 36 = 72
Q.26. The number of common terms in the two sequences: 15, 19, 23, 27, . . . . , 415 and 14, 19, 24, 29, . . . , 464 is
(A) 21
(B) 20
(C) 18
(D) 19
Ans. (B)
Solution:
A: 15, 19, 23, 27, . . . . , 415
B: 14, 19, 24, 29, . . . , 464
Here the first common term = 19
Common difference = LCM of 5, 4 = 20
19+(n - 1)20 ≤ 415
(n-1)20 ≤ 396
(n-1) ≤ 19.8
n = 20
Q.27. Let a, b, x, y be real numbers such that a2 + b2 = 25, x2 + y2 = 169, and ax + by = 65. If k = ay - bx, then
(A) 0 < k ≤ 5/13
(B) k > 5/13
(C) k = 5/13
(D) k = 0
Ans. (D)
Solution:
(ax + by)2 = 652
a2x2 + b2y2 + 2abxy = 652
k = ay − bx
k2 = a2y2 + b2x2 − 2abxy
(a2 + b2)(x2 + y2) = 25 ∗ 169
a2x2 + a2y2 + b2x2 + b2y2 = 25 × 169
k2 = 652 − (25 × 169)
k = 0
D is the correct answer.
Q.28. Mukesh purchased 10 bicycles in 2017, all at the same price. He sold six of these at a profit of 25% and the remaining four at a loss of 25%. If he made a total profit of Rs. 2000, then his purchase price of a bicycle, in Rupees, was
(A) 6000
(B) 8000
(C) 4000
(D) 2000
Ans. (C)
Solution:
Let the cost of each bicycle= 100b
CP of 10 bicycles = 1000b
It is given that he sold six of these at a profit of 25% and the remaining four at a loss of 25%
SP of 10 bicycles = 125b*6+75b*4
= 1050b
Profit = 1050b-1000b = 50b
50b = 2000
CP = 100b = 4000
Q.29. In an examination, the score of A was 10% less than that of B, the score of B was 25% more than that of C, and the score of C was 20% less than that of D. If A scored 72, then the score of D was
Ans. 80
Solution:
Let the score of D = 100d
The score of C = 20% less than that of D = 80d
The score of B = 25% more than C = 100d
The score of A = 10% less than B = 90d
90d = 72
100d = 72*100/90 = 80
Q.30. The salaries of Ramesh, Ganesh and Rajesh were in the ratio 6:5:7 in 2010, and in the ratio 3:4:3 in 2015. If Ramesh’s salary increased by 25% during 2010-2015, then the percentage increase in Rajesh’s salary during this period is closest to
(A) 10
(B) 7
(C) 9
(D) 8
Ans. (B)
Solution:
Let the salaries of Ramesh, Ganesh and Rajesh in 2010 be 6x, 5x, 7x respectively
Let the salaries of Ramesh, Ganesh and Rajesh in 2015 be 3y, 4y, 3y respectively
It is given that Ramesh’s salary increased by 25% during 2010-2015,3y = 1.25*6x
y = 2.5x
Percentage increase in Rajesh's salary = 7.5-7/7=0.07
= 7%
Q.31. Let A and B be two regular polygons having a and b sides, respectively. If b = 2a and each interior angle of B is 3/2 times each interior angle of A, then each interior angle, in degrees, of a regular polygon with a + b sides is
Ans. 150
Solution:
Each interior angle in an n-sided polygon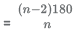
It is given that each interior angle of B is 3/2 times each interior angle of A and b = 2a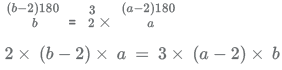
2(ab - 2a) = 3(ab - 2b)
ab - 6b + 4a = 0
a * 2a - 12a + 4a = 0
2a2 − 8a = 0
a(2a - 8) = 0
a cannot be zero so 2a = 8
a = 4, b = 4 * 2 = 8
a + b = 12
Each interior angle of a regular polygon with 12 sides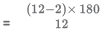
= 150
Q.32. Let f be a function such that f (mn) = f (m) f (n) for every positive integers m and n. If f (1), f (2) and f (3) are positive integers, f (1) < f (2), and f (24) = 54, then f (18) equals
Ans. 12
Solution:
Given, f(mn) = f(m)f(n)
when m = n = 1, f(1) = f(1)*f(1) ⇒ f(1) = 1
when m =1, n = 2, f(2) = f(1)*f(2) ⇒ f(1) = 1
when m = n = 2, f(4) = f(2)*f(2) ⇒ f(4) = [f(2)]2
Similarly f(8) = f(4)*f(2) = [f(2)]3
f(24) = 54
[f(2)]3 [f(3)]= 33 ∗ 2
On comparing LHS and RHS, we get
f(2) = 3 and f(3) = 2
Now we have to find the value of f(18)
f(18) = [f(2)] * [f(3)]2
= 3*4 =12
Q.33. Anil alone can do a job in 20 days while Sunil alone can do it in 40 days. Anil starts the job, and after 3 days, Sunil joins him. Again, after a few more days, Bimal joins them and they together finish the job. If Bimal has done 10% of the job, then in how many days was the job done?
(A) 12
(B) 13
(C) 15
(D) 14
Ans. (B)
Solution:
Let the total work be LCM of 20, 40 = 40 units
Efficiency of Anil and Sunil is 2 units and 1 unit per day respectively.
Anil works alone for 3 days, so Anil must have completed 6 units.
Bimal completes 10% of the work while working along with Anil and Sunil.
Bimal must have completed 4 units.
The remaining 30 units of work is done by Anil and Sunil
Number of days taken by them 30/3 = 10
The total work is completed in 3+10 =13 days
Q.34. In an examination, Rama's score was one-twelfth of the sum of the scores of Mohan and Anjali. After a review, the score of each of them increased by 6. The revised scores of Anjali, Mohan, and Rama were in the ratio 11:10:3. Then Anjali's score exceeded Rama's score by
(A) 26
(B) 32
(C) 35
(D) 24
Ans. B
Solution: Let the scores of Rama, Anjali and Mohan be r, a, m.
It is given that Rama's score was one-twelfth of the sum of the scores of Mohan and Anjali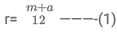
The scores of Rama, Anjali and Mohan after review = r + 6, a + 6, m + 6
a+6:m+6:r+6 = 11:10:3
Let a + 6 = 11x ⇒ a = 11x - 6
m + 6 = 10x ⇒ m =10x - 6
r + 6 = 3x ⇒ r = 3x - 6
Substituting these values in equation (1), we get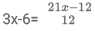
12(3x - 6) = 21x - 12
x = 4
Anjali's score exceeds Rama's score by (a - r) = 8x = 32
|
5 videos|385 docs|204 tests
|




















