Practice Doc: XAT 2019 For Quant | Additional Study Material for CAT PDF Download

Instructions 
For the following questions answer them individually
1. A, B, C, D and E are five employees working in a company. In two successive years, each of them got hikes in his salary as follows:
A : p% and (p+1)%,
B : (p + 2)% and (p - 1)%,
C : (p + 3)% and (p - 2)%,
D : (p + 4)% and (p - 3)%,
E : (p + 5)% and (p - 4)%.
If all of them have the same salary at the end of two years, who got the least hike in his salary?
(A) E
(B) D
(C) C
(D) A
(E) B
Ans. (A)
Solution: 
Let the initial salary of A,B,C,D,E be a, b, c, d, e respectively and let the final salary of everyone be x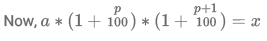




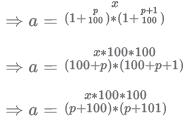
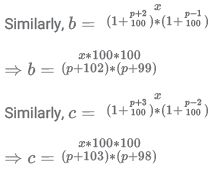
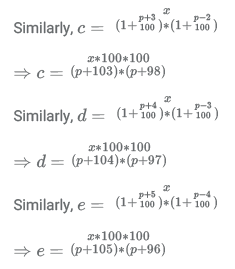
The numerators of the fractions are same, therefore the one with the smallest value of denominator will have the greatest value. If we compare the denominators, we can find out the fraction with the highest value. The person with the highest initial salary got the least raise, as we know that the final salary of all the candidates is same.
Thus, denominator of a, aden = (p + 100) ∗ (p + 101) = p² + 201p + 100 ∗ 101
Similarly, b_den = (p + 102) ∗ (p + 99) = p² + 201p + 102 ∗ 99
c_den = (p + 103) ∗ (p + 98) = p² + 201p + 103 ∗ 98
d_den = (p + 104) ∗ (p + 97) = p² + 201p + 104 ∗ 97
e_den = (p + 105) ∗ (p + 96) = p2 + 201p + 105 ∗ 96
We see that we need to compare only the last terms of the denominators as the other terms are same.
Thus, last term of a, a_lt = 100 ∗ 101 = 100.5² − 0.5²
last term of b, b_lt = 102 ∗ 99 = 100.5² − 1.5²
last term of c, c_lt = 103 ∗ 98 = 100.5² − 2.5²
last term of d, d_lt = 104 ∗ 97 = 100.5² − 3.5²
last term of e, d_lt = 105 ∗ 96 = 100.5² − 4.5²
Thus, we can see that since denominator of is the smallest, therefore E has the highest initial salary.

2. A firm pays its five clerks Rs. 15,000 each, three assistants Rs. 40,000 each and its accountant Rs. 66,000. Then the mean salary in the firm comprising of these nine employees exceeds its median salary by rupees
(A) 14000
(B) 14600
(C) 15200
(D) 15480
(E) 14720
Ans. (A)
Solution: 
There are 9 employees in the firm. Median of any set is the element which occurs in the middle of the set when the elements are positioned in increasing or decreasing order. The number of elements in this set = 5 + 3 + 1 = 9
Thus, the middle element will be in the position 9+1/2 = 5th.
Since we know that the clerks are paid the least so the clerk salaries would be in the beginning of the set if arranged in ascending order. Thus, the 5th element will be a clerk's salary as the number of clerks is 5.
Thus, median of the set = Rs 15,000.
To find the mean salary, we first need to find the sum total salary of the people involved.
Total salary = (Number of clerks*salary of 1 clerk) + (Number of assistants*salary of 1 assistant) + (Number of accountants*salary of 1 accountant)
⇒ Total salary = (5*15,000)+(3*40,000)+(1*66,000)
⇒ Total salary = 75,000+1,20,000+66,000
⇒ Total salary = 2,61,000

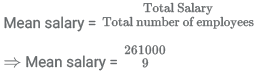
⇒ Mean salary = Rs 29,000 /-

Thus, difference between mean and median salary = 29,000-15,000 = Rs 14,000

3. Two numbers a and b are inversely proportional to each other. If a increases by 100%, then b decreases by:
(A) 200%
(B) 100%
(C) 150%
(D) 80%
(E) 50%
Ans. (E)
Solution: 
Inverse proportionality is expressed as follows :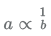

⇒ a*b = constant When value of a changes, the value of b changes accordingly such that their product remains same.
Thus, new value of a a' = a+a = 2a
Thus, the new value of b b' can be solved by :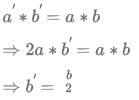

Thus b decreases by 50%.

4.  is a whole number then which one of the statements below is consistent with it?
(A) a = 2, b = 1, c = 1
(B) a = 1, b = 2, c = 2
(C) a = 2, b = 1, c = 2
(D) a = 3, b = 1, c = 1
(E) a = 3, b = 2, c = 1
Ans. (E)
Solution: 
In the given statement, the expression becomes a whole number only when the powers of all the prime numbers are also whole numbers.
Let us first simplify the expression a bit by expressing all terms in terms of prime numbers.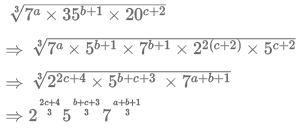

Now, from the given options, we can put in values of the variables and check the exponents of all the numbers.
Option A : a = 2, b = 1, c = 1 :
In this case, we can see that exponent of 5 ie  is not a whole number.
Option B : a = 1, b = 2, c = 2
In this case, we can see that exponent of 2 ie 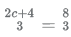 is not a whole number.
Option C : a = 2, b = 1, c = 2
In this case, we can see that exponent of 2 ie 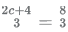 is not a whole number.
Option D : a = 3, b = 1, c = 1
In this case, we can see that exponent of 5 ie 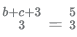 is not a whole number.
Option E : a = 3, b = 2, c = 1
In this case, we can see that all exponents are whole numbers.
Thus, option E is the correct option.

5. A gold ingot in the shape of a cylinder is melted and the resulting molten metal molded into a few identical conical ingots. If the height of each cone is half the height of the original cylinder and the area of the circular base of each cone is one fifth that of the circular base of the cylinder, then how many conical ingots can be made?
(A) 60
(B) 10
(C) 30
(D) 20
(E) 40
Ans. (C)
Solution:
Let the radius of the cylinder be r and height be h (as shown).

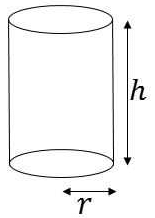
Let the dimensions of the cone be r_c and h_c (as shown).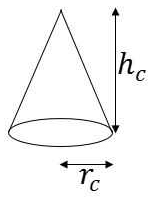

It is given that hc = h/2
Area of base of cone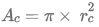

Area of base of cylinder A = π × r²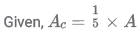


Now we know that the volume of cylinder = total volume of cones
Let the number of cones be n.
So, volume of cylinder = n x volume of each cone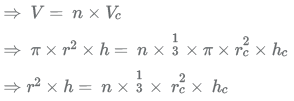


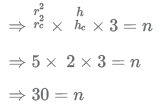
Thus, 30 conical ingots can be made.

6. Given that a and b are integers and that 5x + 2√7 is a root of the polynomial x² - ax + b + 2√7 in x, what is the value of b?
(A) 5
(B) 2
(C) 9
(D) 7
(E) 14
Ans. (A)
Solution: 
Note: For this question, discrepancy is found in question/answer. Full Marks is being awarded to all candidates.

7. An article is marked x% above the cost price. A discount of 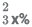 is given on the marked price. If the profit is 4% of the cost price and the value of x lies between 25 and 50, then the value of 50% of x is?
(A) 12
(B) 16
(C) 13
(D) 15
(E) 20
Ans. (D)
Solution:
Let CP of object be a.
It is given that SP 

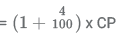
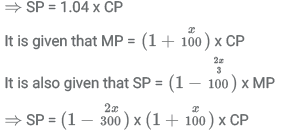
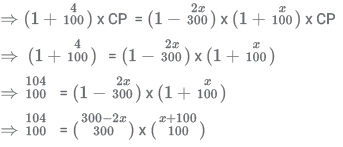
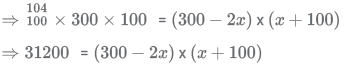
Now, we look at the options.
Since the question says that  x∈[25, 30] so 50% of x ie 0.5x cannot be less than 12.50 ie 25/2 and cannot be more than 25 ie 50/2
This eliminates option A.
Putting values of given in the remaining options in the final expression, [here we need to be careful to use the value of x and not the value of 50% of x as given in the expression] Look carefully in the remaining options : 16,13,15 as 0.5x ie 32,26,30 as possible values of x.
In the question since the discount rate offered is 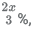 then a safer choice would be to check for the option of 30 in the beginning. It is a safer choice because the percentage of discount that we get in the other options are not whole numbers.
NOTE : THIS IS JUST A SAFE CHOICE AND NEVER MARK AN ANSWER DIRECTLY ON THIS PRESUMPTION WITHOUT CHECKING IT.
Putting x=30 in the expression :
(300 - (2x30))x(30+100) = (300-60)x(100+30) = 240x130 = 24x13x100= 312x100 = 31200= LHS of expression.
Thus the value of is 30.
Therefore value of 50% of = 0.5x30 = 15

8. A computer is sold either for Rs.19200 cash or for Rs.4800 cash down payment together with five equal monthly installments. If the rate of interest charged is 12% per annum, then the amount of each installment (nearest to a rupee) is:
(A) Rs.2880
(B) Rs.2965
(C) Rs.2896
(D) Rs.2990
(E) Rs.3016
Ans. (B)
Solution: 
Amount on which interest will be charged = 19200 - 4800 = 14400
The total amount paid will be equal to the sum of all monthly instalments. Therefore, we have
14400 ∗ k^5a = I (k^4a + k^3a + k^2a + k^a + 1) .....(1)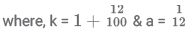

We know that, k^5a − 1 = (k − 1)(k^4a + k^3a + k^2a + k^a + 1)

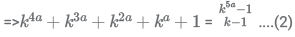
Substituting in equation (1) we get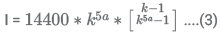

On substituting the values of k and a in equation (3) we get
I ≈ 2965
Hence, option B.

9. When opening his fruit shop for the day a shopkeeper found that his stock of apples could be perfectly arranged in a complete triangular array: that is, every row with one apple more than the row immediately above, going all the way up ending with a single apple at the top.
During any sales transaction, apples are always picked from the uppermost row, and going below only when that row is exhausted.
When one customer walked in the middle of the day she found an incomplete array in display having 126 apples totally. How many rows of apples (complete and incomplete) were seen by this customer? (Assume that the initial stock did not exceed 150 apples.)
(A) 15
(B) 14
(C) 13
(D) 12
(E) 11
Ans. (D)
Solution: 
The stack of apples can be imagined as shown below. For every row, there is an increase of 1 apple from the previous row.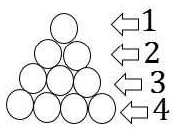

This means that the sum total of the apples present in the stack will be sum of AP given as : 1,2,3,4.... ie the sum of numbers from 1.
This is given by the formula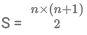

Since the initial number of apples was not more than 150, we find the maximum number of rows that was possible.
Let S be the total initial sum of apples in the cart.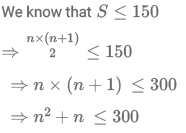

Since the biggest number with square less than 300 is 17, we try to see if 17 works in the expression by hit and trial method.
So, 17 x 18 = 306 > 300, therefore the maximum number of rows possible is not 17.
Since 306 is JUST over 300, let us check at 16.
So, 16 x 17 = 272 < 300, therefore the maximum number of rows possible is 16.
Let us tabulate the total number of apples present in the cart based on the number of rows: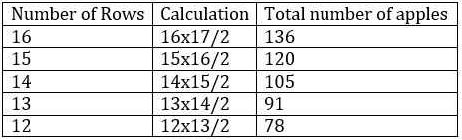

Since the total number of apples from row 15 is less than 126 (which was found by the customer), we can safely say that the total number of rows of apples with the shopkeeper that day was 16.
Now, if 'n' rows of apples are sold, the total available apples can be calculated as :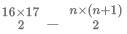

Let us tabulate the result obtained in this case :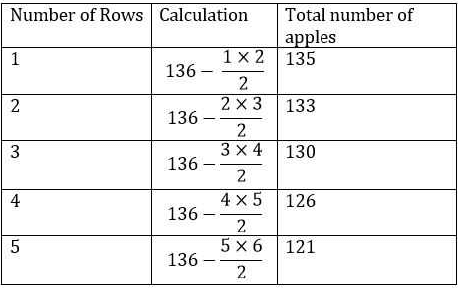

From the table we can see that when the customer saw 126 apples, the apples in the top 4 rows had been sold.
Therefore, the number of rows = 16 - 4 = 12 rows.

10. Let P be the point of intersection of the lines 3x + 4y = 2a and 7x + 2y = 2018 and Q the point of intersection of the lines 3x + 4y = 2018 and 5x + 3y = 1
If the line through P and Q has slope 2, the value of a is:
(A) 4035
(B) 1/2
(C) 3026
(D) 1
(E) 1009
Ans. (C)
Solution: 
On solving for x and y from the equations
3x + 4y = 2018 and 5x + 3y = 1
we get Q(-550,917)
Let, P(x,y)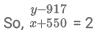

⇒ y - 2x = 2017 ....(1)
Considering the equations
3x + 4y = 2a ........(2)
7x + 2y = 2018 .....(3)
On subtracting equation (2) from (3) we have,
4x - 2y = 2018 - 2a
⇒ 2x - y = 1009 - a
⇒ y - 2x = a -1009 .....(4)
From equation (1) and (4)
2017 = a - 1009
⇒ a = 3026
Hence, option C.

11. Let C be a circle of radius 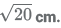 Let L1, L2 be the lines given by 2x − y −1 = 0 and x + 2y − 18 = 0, respectively. Suppose that L1 passes through the center of C and that L2 is tangent to C at the point of intersection of L1 and L2. If (a,b) is the center of C, which of the following is a possible value of a + b?
(A) 11
(B) 17
(C) 8
(D) 20
(E) 14
Ans. (B)
Solution: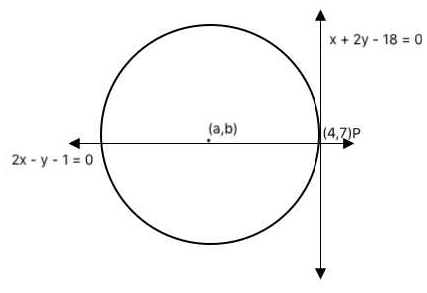

As mentioned in the question,
Lines L1 and L2 intersect at point P as shown in the figure.
On solving for x and y from equations
x + 2y - 18 = 0
2x - y - 1 = 0
We get x = 4 and y = 7.
Given, radius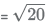
Using the equation of a circle, we have
(4 − a)² + (7 − b)² = 20 ....(1)
The center of the circle will lie on the line: 2x - y - 1 = 0
a,b will satisfy this equation.
So 2a - b - 1= 0
b = 2a - 1
From equation 1...
(4 − a)² + (7 − b)² = 20
(4 − a)² + (8 − 2a)² = 20
5(4 − a)² = 20
a = 6 or a = 2
b = 11 or b = 3
The sum of the coordinates possible = 6 + 11 or 2 + 3
i.e. 17 or 5
Option B is one of the solution.

12.
 equals which of the following?
(A) -5
(B) -2
(C) -4
(D) -3
(E) None of the others
Ans. (C)
Solution: 
Simplify the expression a bit to remove the root sign in the denominator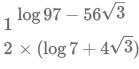


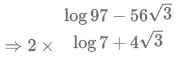
To move further, let us see the root of the numerator.
Assume the root of the numberator to be √a - √b
When we square it, we get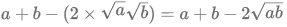

comparing the value of terms under root with the terms in the numerator, we get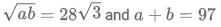

From solving this, we get to know that
a = 7 and b = 4√3
log7 - 4√3
Thus the expression can be written as 2 × 2 × log 7 + 4√3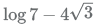


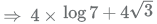
Now, let us look at the reciprocal of the term in log in the denominator.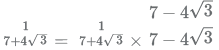




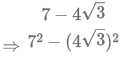
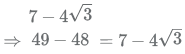
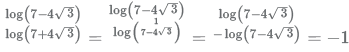
Thus the value of the expression can be further simplified as
⇒ 4 × (−1) = −4
Hence the correct answer is option C

13. In the trapezium ABCD the sides AB and CD are parallel. The value of


(A)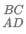
(B)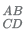
(C)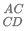
(D)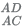
(E)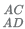
Ans. (D)
Solution:
Construct a perpendicular in the trapezium. Let its height be 'h'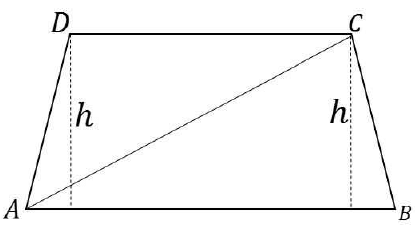



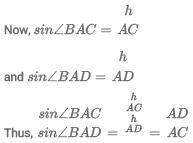
14. In the picture below, EFGH, ABCD are squares, and ABE, BCF, CDG, DAH are equilateral triangles. What is the ratio of the area of the square EFGH to that of ABCD?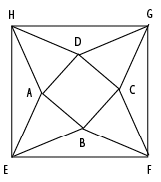

(A) √3 + 2
(B) √2 + √3
(C) 1 + √3
(D) √2 + 2
(E) 3 + √2
Ans. (A)
Solution:
Let the sides of the smaller square be units and the sides of the larger square be y units.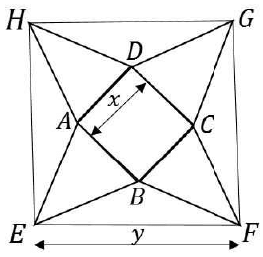

Construct diagonal HF on the larger square. Let the point of intersection of AD and diagonal be I and point of intersection of BC and diagonal be J.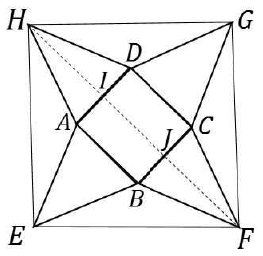

We know that since EFGH is a square, the diagonal will bisect the angle. Therefore ∠EHF = 45º
Observe ΔAEH and ΔDHG :
AE = AH = DH = DG = x units and EH = HG = y units.
Thus by SSS property, ΔAEH ≅ ΔDHG
Thus, we know that ∠AHE = ∠DHG
Also, ∠AHE + ∠DHG + ∠AHD = 90º (angle of a square)
⇒ (2 × ∠AH E) + 60º = 90º (angle of an equilateral triangle)
⇒ (2 × ∠AH E) = 30º
⇒ ∠AHE = 15º
Since ∠AHE = 15º, ∠AH I = 45º − 15º = 30º
Since 30º = 60º/2 we can say that HF is the angle bisector of AHD
Since ΔAHD is an equilateral triangle, we know that the angle bisector, median and altitude will all be the same line ie HI in this case.
By symmetry, we know that JF will also be the angle bisector, median and altitude.
Also, length of altitude of equilateral triangle ie HI and JF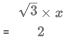

Length of diagonal HF = √2 × y
From the figure, we can express the length of diagonal HF as given :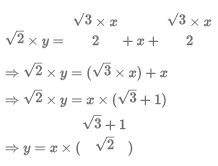

Ratio of areas asked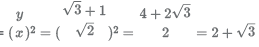


15. What is the maximum number of points that can be placed on a circular disk of radius 1 metre (some of the points could be placed on the bounding circle of the disk) such that no two points are at a distance of less than 1 metre from each other?
(A) 6
(B) 9
(C) 7
(D) 8
(E) 5
Ans. (C)
Solution: 
In order to accommodate maximum number of points on the circular disk, all the points should be placed on the boundary of the disk as any point if placed inside the boundary would be less than 1 metre apart from the centre of the disk. Also, all the points have to be exactly 1 metre apart from each other to place maximum number of points. Hence, a maximum of 6 points can be placed on the boundary of the disk (each adjacent points placed 60 degrees apart) and 1 point at the centre.
Hence, a total of 7 points can be placed on the disk.

16. The figure below shows two right angled triangles ΔOAB and ΔOQP with right angles at vertex A and P, respectively, having the common vertex O, The lengths of some of the sides are indicated in the figure. (Note that the figure is not drawn to scale.) AB and OP are parallel.
What is ∠QOB?

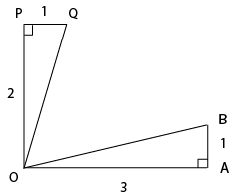
(A) tan⁻¹(2/3)
(B) 45°
(C) 30°
(D) tan⁻¹(3/2)
(E) 60°
Ans. (B)
Solution: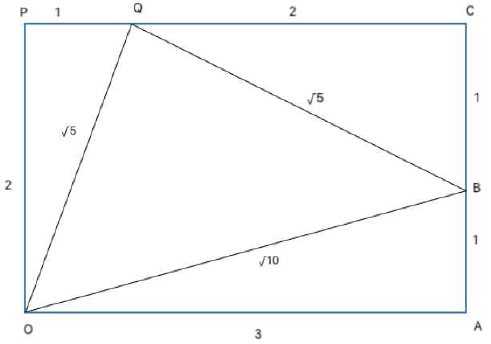

The figure can be redrawn as shown above.
∵ AB and OP are parallel, POAC is a rectangle.
In right QCB, QB = √5
ΔQBO is an isosceles right angled triangle with ∠OQB = 90º = (By Pythagoras theorem)
∴ ∠OQB = 45º

17. Consider the function f(x) = (x + 4)(x + 6)(x + 8) ⋯ (x + 98). The number of integers x for which f(x) < 0 is:
(A) 23
(B) 26
(C) 24
(D) 48
(E) 49
Ans. (C)
Solution: 
The critical points of the function are -4, -6, -8, ... , -98 (48 points).
For all integers less than -98 and greater than -4 f(x) > 0 always . for x= -5, f(x) < 0
Similarly, for x= -9, -13, ...., -97 (This is an AP with common difference -4)
Hence, in total there are 24 such integers satisfying f(x)< 0.

18. Let ABC be an isosceles triangle. Suppose that the sides AB and AC are equal and let the length of AB be x cm. Let b denote the angle ∠ABC and sin b = 3/5. If the area of the triangle ABC is M square cm, then which of the following is true about M?
(A)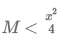
(B)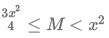
(C)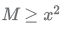
(D)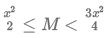
(E)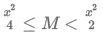
Ans. (E)
Solution: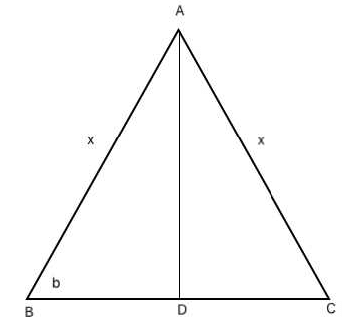

Δ ABC can be represented as shown above where AD ⊥ BC

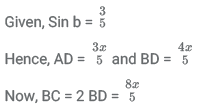
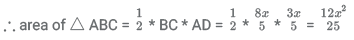
Only option E satisfies.
Hence, option E.

19. If x² + x + 1 = 0, then x²⁰¹⁸ + x²⁰¹⁹ equals which of the following:
(A) x + 1
(B) x
(C) -x
(D)  x - 1
(E) None of the others
Ans. (C)
Solution: We know that,
x³ − 1 = (x − 1)(x² + x + 1)
Since, x² + x + 1 = 0
∴ x³ − 1 = 0
⇒ x³ = 1

= -x
Hence, option C.

20. We have two unknown positive integers m and n, whose product is less than 100.
There are two additional statement of facts available: 
mn is divisible by six consecutive integers { j, j + 1,...,j + 5} m + n is a perfect square.
Which of the two statements above, alone or in combination shall be sufficient to determine the numbers m and n?
(A) Each statement alone is sufficient to answer the question.
(B) Both statements taken together are sufficient to answer the question, but neither statement alone is sufficient.
(C) Statement 2 alone is sufficient, but statement 1 alone is not sufficient to answer the question.
(D) Statements 1 and 2 together are not sufficient, and additional data is needed to answer the question.
(E) Statement 1 alone is sufficient, but statement 2 alone is not sufficient to answer the question.
Ans. (B)
Solution: 
Given, m and n are two positive integers having product less than 100
Statement 1:
mn is divisible by 6 consecutive integers. This means mn must be divisible by the LCM of these 6 integers its multiples.
Only numbers from 1 to 6 satisfy this with LCM 60. Any other set of 6 consecutive integers clearly exceeds 100 as its LCM.
Only such number satisfying the condition is 60. 60 can further be expressed as the product of two positive integers in the following ways: 1 x 60, 2 x 30, 3 x 20, 4 x 15, 5 x 12 and 6 x 10.
So, no unique values of m and n can be determined from the above.
Statement 2:
m + n is a perfect square.
From this statement alone too no unique set of solutions can be determined.
From Statements 1 and 2: Only the pair 6 x 10 satisfies the condition.
Hence, both statements taken together are sufficient to answer the question, but neither statement alone is sufficient.

21. A bag contains marbles of three colours-red, blue and green. There are 8 blue marbles in the bag.
There are two additional statement of facts available: If we pull out marbles from the bag at random, to guarantee that we have at least 3 green marbles, we need to extract 17 marbles.
If we pull out marbles from the bag at random, to guarantee that we have at least 2 red marbles, we need to extract 19 marbles.
Which of the two statements above, alone or in combination shall be sufficient to answer the question "how many green marbles are there in the bag"?
(A) Statement 1 alone is sufficient, but statement 2 alone is not sufficient to answer the question.
(B) Statement 2 alone is sufficient, but statement 1 alone is not sufficient to answer the question.
(C) Statements 1 and 2 together are not sufficient, and additional data is needed to answer the question.
(D) Each statement alone is sufficient to answer the question.
(E) Both statements taken together are sufficient to answer the question, but neither statement alone is sufficient.
Ans. (B)
Solution: 
From statement 1:
Red + Blue + Green = 17 Since, this ensures that there are at least 3 green marbles, so, remaining marbles must be red and blue.
∴ Red + Blue = 17 - 3 = 14
Blue = 14 - Red = 14 - 8 = 6
But, this doesn't give us the total number of green marbles. So, statement 1 alone is not sufficient.
From statement 2:
Red + Blue + Green = 19
Since, this ensures that there are at least 2 red marbles, so, remaining marbles must be blue and green
∴ Blue + Green = 19 - 2 = 17
Again, Green = 17 - Blue = 17 - 8 = 9.
Hence, statement 2 alone is sufficient to answer the question.

Instructions 
The break-up of the students in a university by subject major is given in the polar pie-chart. The bar chart shows the number of students who major in physics by geographic location.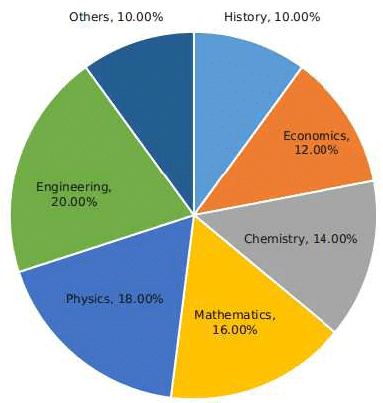
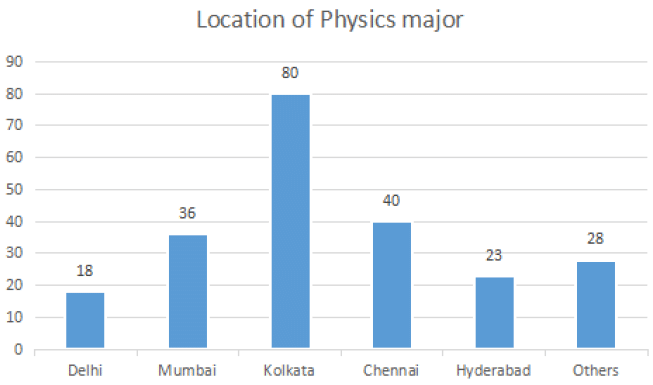22. How many students major in chemistry?
(A) 200
(B) 175
(C) 170
(D) 190
(E) 180
Ans. (B)
Solution: 
Total number of Physics major from all locations = 225
∴ Total number of students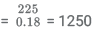

Number of students majoring in chemistry = 14 % * 1250 = 175
Hence, option B.

23. If the proportion of physics majors who are from Delhi is the same as the proportion of engineering majors who are from Delhi, how many engineering majors are from Delhi?
(A) 22
(B) 26
(C) 18
(D) 20
(E) 24
Ans. (D)
Solution:
Total number of Physics major from all locations = 225
∴ Total number of students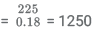

Number of engineering students = 20% * 1250 = 250
So, basis the given condition we have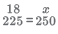

⇒ x = 20
Hence, option D
(Note: This question has been presented as was in the actual paper and has been solved by the aid of visual inference)

24. 12% of all students are from Chennai. What is the largest possible percentage of economics students that can be from Chennai, rounded off to the nearest integer?
(A) 73%
(B) 77%
(C) 75%
(D) 71%
(E) 69%
Ans. (A)
Solution: 
Total number of Physics major from all locations = 225
∴ Total number of students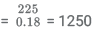

Students from Chennai = 12% * 1250 = 150
Given, number of Physics majors from chennai = 40
∴ maximum possible number of economic students from chennai = 150 - 40 = 110
Maximum percentage of students = * 100 % = 73.33 %
Hence, option A.

Instructions 
Given below is the time table for a trans-continental train that cuts across several time zones. All timings are in local time in the respective cities. The average speed of the train between any two cities is the same in both directions.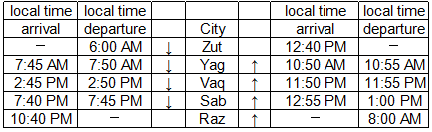

25. Which of the following pairs of cities are in the same time zone?
(A) Yag and Vaq
(B) Vaq and Sab
(C) Zut and Yag
(D) No pair of cities are in the same time zone.
(E) Sab and Raz
Ans. (C)
Solution: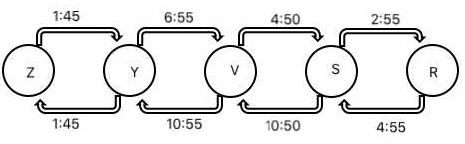

The above figure shows the time taken in hrs:min to travel between two consecutive cities both for upward and downward journeys.
The difference in time between two consecutive cities will be the average of the difference in time taken for upward and downward journeys.
So, the difference of time for different consecutive pairs can be found as below:
Z-Y:
For both up & down motions time difference is 0. Hence, Z & Y are in same time zone.
Y-V:
Time taken for travelling from Y to V is less than that of from V to Y with a difference of 4 hrs. Hence, Y is 2 hours ahead of V.
V-S:
Time taken for travelling from V to S is less than that of from S to V with a difference of 6 hrs. Hence, V is 3 hours ahead of S.
S-R:
Time taken for travelling from S to R is less than that of from R to S with a difference of 2 hrs. Hence, S is 1 hour ahead of R.
As shown above, only cities Zut and Yag are in same time-zone.
Hence, option C.

26. What is the total time taken in minutes by the train to go from Zut to Raz?
(A) 22 hours, 40 minutes
(B) 28 hours, 40 minutes
(C) 16 hours, 40 minutes
(D) 20 hours, 40 minutes 
(E) 24 hours, 40 minutes
Ans. (A)
Solution:

The above figure shows the time taken in hrs:min to travel between two consecutive cities both for upward and downward journeys.
The difference in time between two consecutive cities will be the average of the difference in time taken for upward and downward journeys.
So, the difference of time for different consecutive pairs can be found as below:
Z-Y:
For both up & down motions time difference is 0. Hence, Z & Y are in same time zone.
Y-V:
Time taken for travelling from Y to V is less than that of from V to Y with a difference of 4 hrs. Hence, Y is 2 hours ahead of V.
V-S:
Time taken for travelling from V to S is less than that of from S to V with a difference of 6 hrs. Hence, V is 3 hours ahead of S.
S-R:
Time taken for travelling from S to R is less than that of from R to S with a difference of 2 hrs. Hence, S is 1 hour ahead of R.
Zut is 6 hours ahead of Rag. Also, the train departs from Zut at 6:00 am and arrives at Rag at 10:40 pm taking a total of 16 hrs 40 min.
Hence, the total time taken to travel from Zut to Rag is 22 hrs 40 min.
Hence, option A.

27. What time is it at Yag when it is 12:00 noon at Sab?
(A) 5:00 pm
(B) 12:00 noon
(C) 9:30 am
(D) 7:00 am
(E) 2:30 pm
Ans. (A)
Solution: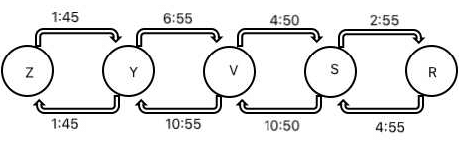

The above figure shows the time taken in hrs:min to travel between two consecutive cities both for upward and downward journeys.
The difference in time between two consecutive cities will be the average of the difference in time taken for upward and downward journeys.
So, the difference of time for different consecutive pairs can be found as below:
Z-Y:
For both up & down motions time difference is 0. Hence, Z & Y are in same time zone.
Y-V:
Time taken for travelling from Y to V is less than that of from V to Y with a difference of 4 hrs. Hence, Y is 2 hours ahead of V.
V-S:
Time taken for travelling from V to S is less than that of from S to V with a difference of 6 hrs. Hence, V is 3 hours ahead of S.
S-R:
Time taken for travelling from S to R is less than that of from R to S with a difference of 2 hrs. Hence, S is 1 hour ahead of R.
It can be concluded that Yag is 5 hours ahead of Sab. Hence, it will be 5:00 Pm at Yag when it is 12 noon at Sab.
Hence, option A.