Practice Doc: XAT 2020 For Quant | Additional Study Material for CAT PDF Download
1. Nalini has received a total of 600 WhatsApp messages from four friends Anita, Bina, Chaitra and Divya. Bina and Divya have respectively sent 30% and 20% of these messages, while Anita has sent an equal number of messages as Chaitra. Moreover, Nalini finds that of Anita’s, Bina’s, Chaitra’s and Divya’s messages, 60%, 40%, 80% and 50% respectively are jokes. What percentage of the jokes, received by Nalini, have been sent neither by Divya nor by Bina?
(A) 65.12
(B) 38.6
(C) 61.4
(D) 57
(E) 34.88
Ans. (C)
2. 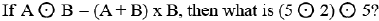
(A) 125
(B) 200
(C) 95
(D) 74
(E) 275
Ans. (C)
3. Two friends, Ram and Shyam, start at the same point, at the same time. Ram travels straight north at a speed of 10km/hr, while Shyam travels straight east at twice the speed of Ram. After 15 minutes, Shyam messages Ram that he is just passing by a large telephone tower and after another 15 minutes Ram messages Shyam that he is just passing by an old banyan tree. After some more time has elapsed, Ram and Shyam stop. They stop at the same point of time. If the straight-line distance between Ram and Shyam now is 50 km, how far is Shyam from the banyan tree (in km)? (Assume that Ram and Shyam travel on a flat surface.)
(A) 45
(B) 20√5 − 5
(C) 20√5 + 5
(D)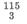
(E)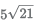
Ans. (A)
4. Two lighthouses, located at points A and B on the earth, are 60 feet and 40 feet tall respectively. Each lighthouse is perfectly vertical and the land connecting A and B is perfectly flat. The topmost point of the lighthouse at A is A’ and of the lighthouse at B is B’. Draw line segments A’B and B’A, and let them intersect at point C’. Drop a perpendicular from C’ to touch the earth at point C. What is the length of CC’ in feet?
(A) 20
(B) 25
(C) 30
(D) 24
(E) The distance between A and B is also needed to solve this
Ans. (D)
5. A man is laying stones, from start to end, along the two sides of a 200-meterwalkway. The stones are to be laid 5 meters apart from each other. When he begins, all the stones are present at the start of the walkway. He places the first stone on each side at the walkway’s start. For all the other stones, the man lays the stones first along one of the walkway’s sides, then along the other side in an exactly similar fashion. However, he can carry only one stone at a time. To lay each stone, the man walks to the spot, lays the stone, and then walks back to pick another. After laying all the stones, the man walks back to the start, which marks the end of his work.
What is the total distance that the man walks in executing this work? Assume that the width of the walkway is negligible.
(A) 16400 metres
(B) 4100 metres
(C) 8050 metres
(D) 16200 metres
(E) 8200 metres
Ans. (A)
6. A rectangular swimming pool is 50 meters long and 25 meters wide. Its depth is always the same along its width but linearly increases along its length from 1 meter at one end to 4 meters at the other end. How much water (in cubic meters) is needed to completely fill the pool?
(A) 2500
(B) 3125
(C) 3750
(D) 1875
(E) 1250
Ans. (B)
7. A shop sells bags in three sizes: small, medium and large. A large bag costs Rs.1000, a medium bag costs Rs.200, and a small bag costs Rs.50. Three buyers, Ashish, Banti and Chintu, independently buy some numbers of these types of bags. The respective amounts spent by Ashish, Banti and Chintu are equal. Put together, the shop sells 1 large bag, 15 small bags and some medium bags to these three buyers. What is the minimum number of medium bags that the shop sells to them?
(A) 5
(B) 9
(C) 4
(D) 10
(E) 7
Ans. (E)
8. In the figure given below, the circle has a chord AB of length 12 cm, which makes an angle of at the center of the circle, O. ABCD, as shown in the diagram, is a rectangle. OQ is the perpendicular bisector of AB, intersecting the chord AB at P, the arc AB at M and CD at Q. OM = MQ. The area of the region enclosed by the line segments AQ and QB,and the arc BMA, is closest to (in cm2):
(A) 215
(B) 137
(C) 35
(D) 63
(E) 69
Ans. (E)
Instructions
Read the information given below and answer the 3 associated questions.
During 2015-2019, the revenues of four companies P-S were as follows: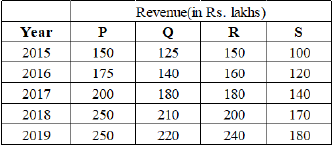
9. Which of the given companies has seen the highest year-on-year growth (in percentage) in any single year during this five-year period?
(A) P
(B) There was a tie among multiple companies
(C) R
(D) Q
(E) S
Ans. (D)
10. It was discovered later that one of the companies misreported its revenue of one of the years. If the misreported revenue is replaced by the correct revenue, the revenues of that company over the five-year period will be in an arithmetic progression. The company that misreported its revenue was
(A) R or S
(B) S only
(C) P or R
(D) P or S
(E) P only
Ans. (D)
11. During the period from 2014 to 2015, the revenue increased by 25% for three of the companies and by 50% for the remaining company. The total increase in revenue, for all four companies put together, was Rs. 125 lakhs.
Which of the following CANNOT be true?
(A) From 2014 to 2015, the increases in revenues of at least two companies were the same
(B) The revenue of Q in 2014 was the same as the revenue of R in 2014
(C) The company that experienced the 50% increase in revenue also experienced the maximum increase in revenue in absolute terms
(D) The 2014 revenues of P and R cannot be determined uniquely
(E) From 2014 to 2015, the revenues of P and R increased by different amounts
Ans. (A)
12. A box contains 6 cricket balls, 5 tennis balls and 4 rubber balls. Of these, some balls are defective. The proportion of defective cricket balls is more than the proportion of defective tennis balls but less than the proportion of defective rubber balls.
Moreover, the overall proportion of defective balls is twice the proportion of defective tennis balls. What BEST can be said about the number of defective rubber balls in the box?
(A) It is either 2 or 3
(B) It is exactly 2
(C) It is exactly 3
(D) It is either 3 or 4
(E) It is either 0 or 1
Ans. C
13. When expressed in a decimal form, which of the following numbers will be non - terminating as well as non-repeating?
(A) 
(B) sin2 1∘ + sin2 2∘ + .... + sin2 89∘
(C) 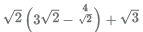
(D) 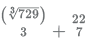
(E) 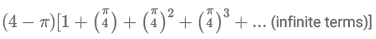
Ans. (C)
14. A rectangular field is 40 meters long and 30 meters wide. Draw diagonals on this field and then draw circles of radius 1.25 meters, with centers only on the diagonals. Each circle must fall completely within the field. Any two circles can touch each other but should not overlap. What is the maximum number of such circles that can be drawn in the field?
(A) 38
(B) 39
(C) 36
(D) 37
(E) 40
Ans. D
15. A hare and a tortoise run between points O and P located exactly 6 km from each other on a straight line. They start together at O, go straight to P and then return to O along the same line. They run at constant speeds of 12 km/hr and 1 km/hr respectively. Since the tortoise is slower than the hare, the hare shuttles between O and P until the tortoise goes once to P and returns to O. During the run, how many times are the hare and the tortoise separated by an exact distance of 1 km from each other?
(A) 24
(B) 42
(C) 22
(D) 48
(E) 40
Ans. E
16. Consider the four variables A, B, C and D and a function Z of these variables, It is given that A, B, C and D must be non-negative integers and thatall of the following relationships must hold:
(i) 2A + B ≤ 2
(ii) 4A + 2B + C ≤ 12
(iii) 3A + 4B + D ≤ 15
If Z needs to be maximised, then what value must D take?
(A) 15
(B) 12
(C) 0
(D) 10
(E) 5
Ans. (B)
17. XYZ is an equilateral triangle, inscribed in a circle. P is a point on the arc YZ such that X and P are on opposite sides of the chord YZ.
Which of the following MUST always be true?
(A) XZ + YP = XY + PZ
(B) XP = XY
(C) XP + PZ = XY + YP
(D) XP = YP + PZ
(E) XP = XY + YZ
Ans. (D)
18. X, Y and Z start a web-based venture together. X invests Rs. 2.5 lakhs, Y invests Rs. 3.5 lakhs, and Z invests Rs. 4 lakhs. In the first year, the venture makes a profit of Rs. 2 lakhs. A part of the profit is shared between Y and Z in the ratio of 2:3, and the remaining profit is divided among X, Y and Z in the ratio of their initial investments. The amount that Z receives is four times the amount that X receives. How much amount does Y receive?
(A) Rs. 102,500
(B) Rs. 93,750
(C) Rs. 74,250
(D) Rs. 75,000
(E) Rs. 80,200
Ans. (D)
19. Mohanlal, a prosperous farmer, has a square land of side 2 km. For the current season, he decides to have some fun. He marks two distinct points on one of the diagonals of the land. Using these points as centers, he constructs two circles. Each of these circles falls completely within the land, and touches at least two sides of the land. To his surprise, the radii of both the circles are exactly equal to 2/3 km. Mohanlal plants potatoes on the overlapping portion of these circles. Calculate the area on which Mohanlal planted potatoes (in sq. km).
(A) 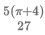
(B) 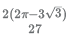
(C) 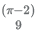
(D) 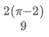
(E) 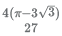
Ans. (D)
Instructions
Read the information given below and answer the 2 associated questions.
190 students have to choose at least one elective and at most two electives from a list of three electives: E1, E2 and E3. It is found that the number of students choosing E1 is half the number of students choosing E2, and one third the number of students choosing E3.
Moreover, the number of students choosing two electives is 50.
20. Which of the following CANNOT be obtained from the given information?
(A) Number of students choosing E1
(B) Number of students choosing either E1 or E2 or both, but not E3
(C) Number of students choosing both E1 and E2
(D) Number of students choosing E3
(E) Number of students choosing exactly one elective
Ans. C
21. In addition to the given information, which of the following information is NECESSARY and SUFFICIENT to compute the number of students choosing only E1, only E2 and only E3?
(A) Number of students choosing only E2, and number of students choosing both E2 and E3
(B) Number of students choosing both E1 and E2, number of students choosing both E2 and E3, and number of students choosing both E3 and E1
(C) Number of students choosing only E1, and number of students choosing both E2 and E3
(D) No extra information is necessary
(E) Number of students choosing both E1 and E2
Ans. (A)
22. Ashok has a bag containing 40 cards, numbered with the integers from 1 to 40. No two cards are numbered with the same integer.
Likewise, his sister Shilpa has another bag containing only five cards that are numbered with the integers from 1 to 5, with no integer repeating. Their mother, Latha, randomly draws one card each from Ashok’s and Shilpa’s bags and notes down their respective numbers. If Latha divides the number obtained from Ashok’s bag by the number obtained from Shilpa’s, what is the probability that the remainder will not be greater than 2?
(A) 0.8
(B) 0.91
(C) 0.73
(D) 0.94
(E) 0.87
Ans. (E)
Solution:
The number of ways of selecting one card from Ashok's bag and other from Shilpa bag = 40C1 x 5C1 = 200
Now, if the card taken from Shilpa's bag shows 1, then 1 will divide all the numbers o Ashok's card. Hence, the number of ways = 40
If the card taken from Shilpa's bag shows 2, then the remainder will be either 0 or 1. Hence, the number of ways = 40
If the card taken from Shilpa's bag shows 3, then the remainder will be 0, 1 or 2. Hence, the number of ways = 40
If the card taken from Shilpa's bag shows 4, then the remainder will be 0, 1, 2 or 3. So the numbers having 3 as remainder will be rejected. So the number of form 4n + 3 will be rejected. Total number of such numbers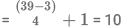
If the card taken from Shilpa's bag shows 5, then the remainder will be 0, 1, 2, 3 or 4. So the numbers having 3 or 4 as remainder will be rejected. So the number of form 5n + 3, 5n+4 will be rejected. Total number of such terms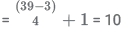
The numbers left = 40 - 10 = 30
The total numbers having 5n + 3 form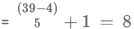
The total numbers having 5n + 4 form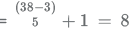
The numbers left = 40 - 8 - 8 = 24
Hence, the probability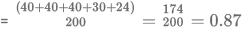
23. X, Y, and Z are three software experts, who work on upgrading the software in a number of identical systems. X takes a day off after every 3 days of work, Y takes a day off after every 4 days of work and Z takes a day off after every 5 days of work.
Starting afresh after a common day off,
(i) X and Y working together can complete one new upgrade job in 6 days
(ii) Z and X working together can complete two new upgrade jobs in 8 days
(iii) Y and Z working together can complete three new upgrade jobs in 12 days If X, Y and Z together start afresh on a new upgrade job (after a common day off), exactly how many days will be required to complete this job?
(A) 3 days
(B) 4 days
(C) 2 days
(D) 3.5 days
(E) 2.5 days
Ans. (E)
24. What is the remainder if is 1920 - 2019 divided by 7?
(A) 5
(B) 0
(C) 3
(D) 1
(E) 6
Ans. A
25. Six drums are used to store water. Five drums are of equal capacity, while the sixth drum has double the capacity of each of these five drums. On one morning, three drums are found half full, two are found two-thirds full and one is found completely full. It is attempted to transfer all the water to the smaller drums. How many smaller drums are adequate to store the water?
(A) Three but not two
(B) Four but not three
(C) Three or four, depending on which drum had how much water initially
(D) Five but not four
(E) Five may be inadequate, depending on which drum had how much water initially
Ans. (D)
Instructions
Read the information given below and answer the 3 associated questions.
The following graph depicts sector-wise percentage contributions to the gross domestic product (GDP) of nine nations, labelled “Nation A”, “Nation B” and so on. It is known that these nations are Brazil, China, France, Germany,India, Japan, Russia, the UK and the USA, but not necessarily in the same order.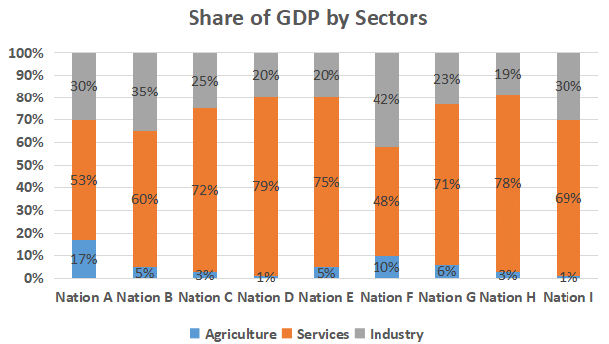 The following, however, are known:
The following, however, are known:
(i) The GDPs of the nine nations (in US $ trillion) are:
(ii) China has the highest agriculture sector GDP, valued at US $1 trillion, followed respectively by the USA and India
(iii) In terms of percentage contribution to the respective nations’ GDPs by their service sectors, the UK and France are respectively the first and the second
(iv) Nation A, Nation B and Nation G have the same GDP
(v) The GDPofIndia’s industry sector is lower than the GDP of Russia’s industry sector. However,it is larger than that of Brazil's industry sector
26. Based on the given information, how many nations can be uniquely identified?
(A) 6
(B) 9
(C) 3
(D) 2
(E) 7
Ans. (A)
27. Based on the given information, which of the following CANNOT be ruled out?
(A) US is Nation I
(B) Russia is Nation G
(C) China is Nation C
(D) Japan is Nation E
(E) India is Nation B
Ans. D
28. Which of the following information, when considered in addition to the given information, does not allow us to completely identify the nine nations in the graph?
(A) Germany’s industry GDP is US $1.2 trillion
(B) The nation ranked fourth in terms of agriculture GDP has its agriculture GDP valued at US $150 billion
(C) In terms of percentage contribution to the respective nations’ GDP, France and Japan’s agriculture sectors contribute the same
(D) Japan’s industry GDP is US $1.25 trillion E Both Japan’s and Germany’s industry GDPs are more than US $1 trillion
Ans. (A)
|
5 videos|385 docs|204 tests
|















