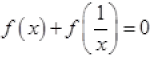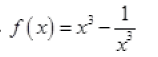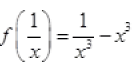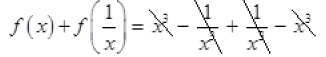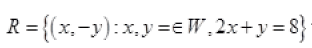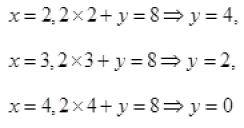Ques 1: Find a and b if (a – 1, b + 5) = (2, 3)If A = {1,3,5}, B = {2,3} find : (Question-2, 3)
(i) A × B
(ii) Let A = {1,2}, B = {2,3,4}, C = {4,5}
(iii) A × (B ∩ C)
(iv) A × (B ∪ C)
Ans: a = 3, b = -2
(i) A × B = {(1,2), (1,3), (3,2), (3,3), (5,2), (5,3)}
(ii) B × A = { (2,1), (2,3), (2,5), (3,1), (3,3), (3,5)}
(ii) {(1,4), (2,4)}
(iv) {(1,2), (1,3), (1,4), (1,5), (2,2), (2,3), (2,4), (2,5)}
Ques 2: If P = {1,3}, Q = {2,3,5}, find the number of relations from A to B
Ans: 26 = 64
Ques 3: If A = {1,2,3,5} and B = {4,6,9}, R = {(x, y) : |x – y| is odd, x ∈ A, y ∈ B} Write R in roster form
(i) R = { (1,1), (2,2), (3,3), (4,4), (4,5)}
(ii) R = { (2,1), (2,2), (2,3), (2,4)}
Which of the following relations are functions. Give reason.
Ans: R = { (1,4), (1,6), (2,9), (3,4), (3,6), (5,4), (5,6)}
(i) Not a function because 4 has two images.
(ii) Not a function because 2 does not have a unique image.
Ques 4: If A and B are finite sets such that n(A) = m and n(B) = K find the number of relations from A to B
Ans: Linen n(A) = n and n(B) = k
∴ n(A * B)= ∩(A) * ∩(B)= mk
∴ the number of subsets of A x B = 2mk
∵ n(A) =m, then the number of subsets of A = m2
Since every subset of A * B is a relation from A to B therefore the number of relations from A to B = 2mk
Ques 5: Let f = {(1,1),(2,3),(0,-1),(-1,3),........} be a function from z to z defined f(x) ax +b, by for same integers a and b determine a and b.
Ans: Given f(x) ax +b
Since (1,1) ∈ f1f(1) = 1 ⇒ a+b = 1.......(i)
(2,3) ∈ f.f (2) = 3 ⇒ 2a+b =3........(ii)
Subtracting (i) from(ii) we set a=2
Substituting a = 2 is (ii) we get 2+b=1
⇒ b = -1
Hence a = 2, b = -1
Ques 6: Express {(x,y): y+ 2x =5, xy ∈ w} as the set of ordered pairs
Ans: Since and x, y ∈ w,
Put x=0, y+0= 5 ⇒ y=5
x=1, y+2*1= 5⇒ y =3
x=2,y+2*2=5 ⇒ y=1
For anther values of x∈w , we do not get y∈w
Hence the required set of ordered peutes is {(0'5),(1,3),(2,1)}
Ques 7: If A = {1,2}, find (A*A*A)
Ans: A*A*A ={(1,1,1),(1,1,2),(1,2,1),(2,1,1),(2,2,1),(2,2,2)}
Ques 8: Let f = [(0,-5),(1,-2),(2,1),(3,4), (4,7)}j be a linear function from z into= find
Ans: f(x) =3x -5
Ques 9: If the ordered pairs (x-2,2y +1) and (y- 1,x+2) are equal, find x&Y
Ans: x=3, y=2
Ques 10: Let A = {-1,2,5,8}, B= {o,1,3,6,7} and R be the relation, is one less than from A to B then find domain and Range of R
Ans: Given A= {-1,2,5,8}, B= {o,1,3,6,7} and R is the relation 'is one less than' from
A to B therefore R = [ (-1,0),(2,3),(5,6) ]
Domain of R = {-1,2,5} and range of R = {0,3,6}
Ques 11: Let R be a relation from N to N define by
 .
.
Is the following true implies a,b ∈ R implies (b,a) ∈ R
Ans: No; let a = 4, b = 2 As 4 = 22, so (4,2) ∈ but 2 ≠ 42 so (2,4) ∈ R
Ques 12: Let be the set of natural numbers and the relation R be define in N by R =  what is the domain, co domain and range of ? Is this relation a function?
what is the domain, co domain and range of ? Is this relation a function?
Ans: Given R =
∴ Domain of R = N. co domain of R = N and Range of R is the set of even natural numbers.
Since every natural number x has a unique image 2x therefore, the relation R is a function.
Ques 13: 40.Let R = {(x,y): y = x +1} and y ∈{0,1,2,3,4,5} list the element of R
Ans: R= {(-1,0),(0,1),(1,2),(2,3),(3,4),(4,5)}
Ques 14: Let f be the subset of  defined by
defined by
 is f a function
is f a function  justify your answer
justify your answer
Ans: f Is not a function from Q to Z.

∴ One element 1/2 have two images
∴ f is not function
Ques 15: The function 'f' which maps temperature in Celsius into temperature in Fahrenheit is defined by 
Ans:

f (o) = 32
Ques 16: If  Prove that
Prove that

Ans:



= 0
Ques 17: If A and B are two sets containing m and n elements respectively how many different relations can be defined from A to B ?
Ans: 2m+n
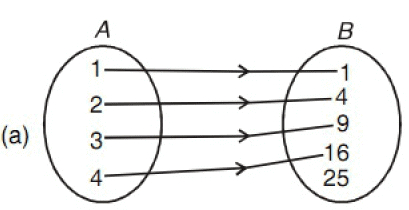
Ques 18: Let A = {1,2,3,4}, B = {1,4,9,16,25} and R be a relation defined from A to B as, R = {(x, y) : x ϵ A, y ϵ B and y = x2}
(a) Depict this relation using arrow diagram.
(b) Find domain of R.
(c) Find range of R.
(d) Write co-domain of R.
Ans:

(b) {1,2,3,4}
(c) {1,4,9,16}
(d) {1,4,9,16,25}
Ques 19: Let R = { (x, y) : x, y ϵ N and y = 2x} be a relation on N. Find :
(i) Domain
(ii) Codomain
(iii) Range Is this relation a function from N to N
Ans: (i) N
(ii) N
(iii) Set of even natural numbers yes, R is a function from N to N.
Ques 20: Find the domain and range of, f(x) = |2x – 3| – 3
Ans: Domain is R
Range is [–3, ∞)
Ques 21: Draw the graph of the Constant function, f : R ϵ R; f(x) = 2 x ϵ R. Also find its domain and range.
Ans: Domain = R
Range = {2}
Ques 22: Let 
Then
(i) Find the domain and the range of R
(ii) Write R as a set of ordered pairs.
Ans: (i) Given 2x + y = 8 and x y ϵ w
Put


for all the values x y ϵ w we do not get y ϵ w
∴ domain of R = {0,1,2,3,4} and range of R = {8,6,4,2,0}
(ii) R as a set of ordered pairs can be written as

 .
.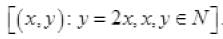 what is the domain, co domain and range of ? Is this relation a function?
what is the domain, co domain and range of ? Is this relation a function?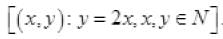
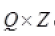 defined by
defined by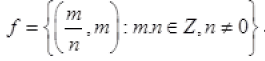 is f a function
is f a function 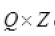 justify your answer
justify your answer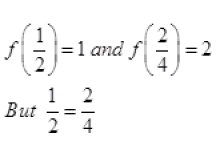
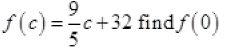
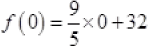
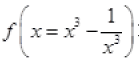 Prove that
Prove that