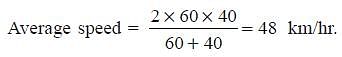This EduRev document offers 20 Multiple Choice Questions (MCQs) from the topic Averages (Level - 1). These questions are of Level - 1 difficulty and will assist you in the preparation of CAT & other MBA exams. You can practice/attempt these CAT Multiple Choice Questions (MCQs) and check the explanations for a better understanding of the topic.
Question for Practice Questions Level 1: Averages - 2
Try yourself:The average of the first ten prime numbers, which are odd, is
Explanation
Required average = (3 + 5 + 7 + 11 + 13 + 17 + 19
+ 23 + 29 + 31)/10 = 158/10 = 15.8.
Report a problem
Question for Practice Questions Level 1: Averages - 2
Try yourself:The average weight of 3 boys A, B and C is 74 kg. Another boy D joins the group and the average now becomes 70 kg. If another boy E, whose weight is 3 kg more than that of D, replaces A then the average weight of B, C, D and E becomes 75 kg. The weight of A is
Explanation
D’s weight = 4 x 70 – 3 x 74 = 280 – 222 = 58.
E’s weight = 58 + 3 = 61.
Now, we know that A + B + C + D = 4 x 70 = 280
and B + C + D + E = 75 x 4 = 300. Hence, A’s
weight is 20 kg less than E ’s weight. A = 61 - 20
= 41 kg.
Report a problem
Question for Practice Questions Level 1: Averages - 2
Try yourself:The average of the first ten whole numbers is
Explanation
Required average = (0 + 1 + 2 + … + 9)/10 = 45/10
= 4.5
Report a problem
Question for Practice Questions Level 1: Averages - 2
Try yourself:The average of the first ten odd numbers is
Explanation
The sum of the first n odd numbers = n2. In this case n = 10 → Sum = 102 = 100.
Required average = 100/10 = 10.
Report a problem
Question for Practice Questions Level 1: Averages - 2
Try yourself:The average of the first ten composite numbers is
Explanation
Required average = (4 + 6 + 8 + 9 + 10 + 12 + 14 + 15 + 16 + 18)/10 = 112/10 = 11.2.
Report a problem
Question for Practice Questions Level 1: Averages - 2
Try yourself:The average age of 13 boys and the principal is 10 years. When the principal’s age is excluded, the average age decreases by 2 year. What is the age of the principal?
Explanation
P = 14 x 10 – 13 x 8 = 140 –104 = 36
Report a problem
Question for Practice Questions Level 1: Averages - 2
Try yourself:The mean temperature of Monday to Wednesday was 35 °C and of Tuesday to Thursday was 30 °C. If the temperature on Thursday was ½ that of Monday, the temperature on Thursday was
Explanation
Monday + Tuesday + Wednesday = 3 x 35 = 105;
Tuesday + Wednesday + Thursday = 3 x 30 = 90.
Thus, Monday – Thursday = 15 and
Thursday = Monday/2 → Monday = 30 and Thursday = 15
Report a problem
Question for Practice Questions Level 1: Averages - 2
Try yourself:Ganguly has a certain average for 4 innings. In the 5th inning, he scores 40 runs thereby increasing his average by 4 runs. His new average is
Explanation
4x + 40 = 5(x + 4) → x = 20 (average after 4 innings).
Hence, new average = 20 + 4 = 24.
Report a problem
Question for Practice Questions Level 1: Averages - 2
Try yourself:There are three fractions A, B and C. If A = 1/5 and B = 1/8 and the average of A, B and C is 1/10. What is the value of C?
Explanation
1/5 + 1/8 + C = 3 x 1/10 → C = –1/40.
Report a problem
Question for Practice Questions Level 1: Averages - 2
Try yourself:The average monthly expenditure of a family was 2250 for the first 3 months, ₹ 2150 for the next three months and ₹ 5750 for the next three months. Find the average income of the family for the 9 months, if they save ₹ 500 per month.
Explanation
Average income over 9 months = [3 x (2250 + 500) + 3 x (2150 + 500) + 3 x (5750+500)]/9 = 3883.33
Report a problem
Question for Practice Questions Level 1: Averages - 2
Try yourself:The average age of 5 persons in a group is increased by 10 years when two men aged 30 years and 40 years are substituted by two women. Find the average age (in years) of the two women.
Explanation
If the average age of 5 persons has gone up by 10 years it means the total age has gone up by 50 years.
Thus the total age of the two women would be: 30 + 40 + 50 = 120. Hence, their average age = 60 years.
Report a problem
Question for Practice Questions Level 1: Averages - 2
Try yourself:The speed of the train in going from Kanpur to Lucknow is 60 km/hr while when coming back from Lucknow to Kanpur, its speed is 40 km/hr. Find the average speed (in km/hr) during the whole journey.
Explanation
Report a problem
Question for Practice Questions Level 1: Averages - 2
Try yourself:Five years ago, the average age of A, B and C was 25 years and that of B and C 10 years ago was 20 years. A’s present age is
Explanation
Total present age of A, B and C = 25 x 3 + 15 = 75 + 15 = 90.
Total present age of B and C = 20 x 2 + 20 = 60.
A ’s age = 90 – 60 = 30.
Report a problem
Question for Practice Questions Level 1: Averages - 2
Try yourself:The average of the first six multiples of 5 is
Explanation
(5+10+15+20+25+30)/6 = 105/6 = 17.5
Report a problem
Question for Practice Questions Level 1: Averages - 2
Try yourself:The marks obtained by Alan in Mathematics, English and Biology are respectively 90 out of 100, 70 out of 150 and 150 out of 200. Find his average score in percent.
Explanation
His total score is 90 + 70 + 150 = 310 out of 450.
This works out to a percentage score of = 68.88%
Report a problem
Question for Practice Questions Level 1: Averages - 2
Try yourself:The average age of a family of 5 members is 20 years. If the age of the youngest member be 5 years, what was the average age of the family at the birth of the youngest member?
Explanation
Total age (at present) = 5 ¥ 20 = 100 years. Total age of the family excluding the youngest member (for the remaining 5 people) = 100 –5 = 95. Average age
of the other 4 people in the family = 95/4 years.
5 years ago their average age = 95/4 – 5 = 75/4 = 18.75 years.
Report a problem
Question for Practice Questions Level 1: Averages - 2
Try yourself:The average temperature for Wednesday, Thursday and Friday was 20°C. The average for Thursday, Friday and Saturday was 21 °C. If the temperature on Saturday was 22°C, what was the temperature on Wednesday?
Explanation
W + T + F = 60; T + F + S = 63 → S – W = 3.
Hence temperature on Wednesday = 22 – 3 = 19.
Report a problem
Question for Practice Questions Level 1: Averages - 2
Try yourself:The average weight of a class of 19 students is 20 kg. If the weight of the teacher be included, the average rises by 1 kg. What is the weight of the teacher?
Explanation
Teacher’s weight = 21 x 20 – 20 x 19 = 420– 380 = 40.
Report a problem
Question for Practice Questions Level 1: Averages - 2
Try yourself:The average weight of 29 men in a ship is increased by 5 kg when one of the men, who weighs 120 kg, is replaced by a new man. Find the weight of the new man (In kg)
Explanation
The weight of the new man would be 29 x 5 kgs more than the weight of the man he replaces. New man’s weight = 120 + 29 x 5 = 265 kgs.
Report a problem
Question for Practice Questions Level 1: Averages - 2
Try yourself:Find the average of the first 100 natural numbers.
Explanation
The average would be given by the average of the first and last numbers (since the series 1, 2, 3, 4…100 is an Arithmetic Progression).
Hence, the average = (1 + 100)/2 = 50.50
Report a problem