This EduRev document offers 15 Multiple Choice Questions (MCQs) from the topic Binary Logic (Level - 1). These questions are of Level - 1 difficulty and will assist you in the preparation of CAT & other MBA exams. You can practice/attempt these CAT Multiple Choice Questions (MCQs) and check the explanations for a better understanding of the topic.
Question for Practice Questions Level 1: Binary Logic
Try yourself:Three persons Bryan, Edward and Avril, each of whom is of a different community, are standing together. When asked about their community, Bryan replied, "I am a Gitty. Avril is Amora.". Then Edward belongs to which community?
Explanation
In the given statement, Bryan said that he was a Gitty. No truth-teller or liar can make a statement that he is a Gitty (always a lie). Bryan must be an alternator, that is, a Pixie; and his first statement is a lie. Hence, his second statement is true; Avril is an Amora. Edward is a Gitty.
Report a problem
Question for Practice Questions Level 1: Binary Logic
Try yourself:Each of three different persons Mary, Helen and Patricia belong to a different community. In the conversation, Patricia said, "I am a Pixie. Mary is not a Gitty.'' Who among the three persons is an Amora?
Explanation
From the given statement, Patricia cannot be an Amora. He cannot be a Gitty, as if he is a Gitty, his second statement will be true, which is a contradiction. Hence, Patricia must be a Pixie and Mary is a Gitty. Helen is an Amora.
Report a problem
Question for Practice Questions Level 1: Binary Logic
Try yourself:If Bruce is not a Pixie, then who among the three persons is the Gitty?
Explanation
Case 1: Assuming Hamish to be Amora
Hamish:
I am an Amora. ---TRUE
Bruce is an Amora. --TRUE
This is a contradiction, as 2 people cannot be from the same community.
Case 2: Assuming Hamish to be Gitty
I am an Amora. ---FALSE
Bruce is an Amora. --FALSE
This means Bruce must be from Pixie, since Bruce is not from Amora and Hamish is already assumed to belong to Gitty.
But the question says that Bruce is not from Pixie. Hence, this case is also disregarded .
Case 3: Assuming Hamish to be Pixie
I am an Amora. ---FALSE
Bruce is an Amora. --TRUE
Thus, Bruce is an Amora, Hamish is Pixie, and Colin is Gitty.
Case 4: Assuming Hamish to be Pixie
I am an Amora. ---TRUE
Bruce is an Amora. --FALSE
This is not possible since then Hamish would again belong to both Pixie and Amora.
Thus, only Case 3 is valid.
Report a problem
Question for Practice Questions Level 1: Binary Logic
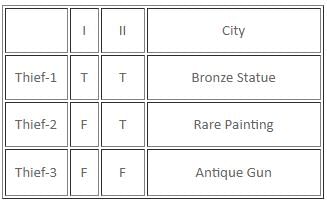
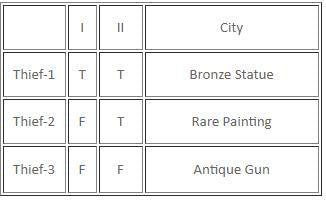
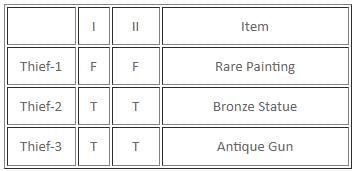
Try yourself:Who among the three must have stolen Antique Gun?
Explanation
Report a problem
Question for Practice Questions Level 1: Binary Logic
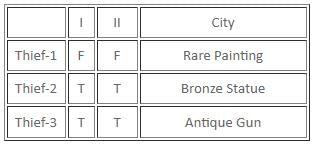
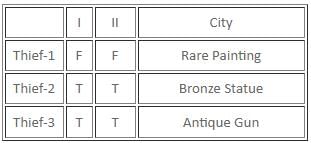
Try yourself:Which item did Thief-2 steal?
Explanation
The only posisble scenario is :
Case 2:
Thief-1:
I stole Bronze Statue. TRUE
Thief-2 stole Rare Painting. TRUE
Thief-2:
I stole Bronze Statue. FALSE
Thief-3 stole Antique Gun. TRUE
Thief-3:
Thief-1 stole Rare Painting. FALSE
Thief-2 stole Bronze Statue. FALSE
Hence, ans is 3.
Report a problem
Question for Practice Questions Level 1: Binary Logic
Try yourself:If there are exactly two thieves who always tell the truth and the third thief either always lies or alternates between the truth and a lie, then which of the following statements must be false?
Explanation
Report a problem
Question for Practice Questions Level 1: Binary Logic
Try yourself:Which team is the Defender playing for?
Explanation
It is given that every player spoke exactly two false statements, hence one true statement. Let the first statement of Stanley be true. Hence, the other two must be false. Therefore, Stanley is not playing for Team-A. Owen is not a Mid-fielder and Geoffrey is not playing for Team-C.
Owen's second statement is therefore true. Hence, his first and third statements must be false. Hence, Owen is not a Defender and Stanley is not a Mid-fielder. Owen has to be a Goalkeeper. Stanley should be a Defender. Geoffrey must be a Mid-fielder.
Hence, Geoffrey's last statement is true. But Geoffrey's first statement is also true. Since this is not possible, Stanley's first statement cannot be true.
Let the second statement of Stanley be true. Therefore, Owen is a Mid-fielder. From his other two statements, we can say that Stanley is from Team-A and Geoffrey is from Team-B. Hence, Owen is from Team-C. Owen's second statement is true. His first and third statements are false. Geoffrey's second statement is true. His first and third statements must be false. Therefore, Stanley must be a Goalkeeper and Geoffrey must be a Defender. This is one possible case.
Let Stanley's third statement be true. Geoffrey must be from Team-C. From his first statement, we get that Stanley must be from Team-A. Therefore, Owen must be from Team-B. Owen is not a Mid-fielder.
Owen's second statement and Geoffrey's second statement are false. The only case possible in which both Owen and Geoffrey tell one true statement each is when Owen's first statement and Geoffrey's third statement are true. Hence, Owen is a Defender, Geoffrey is a Mid-fielder and Stanley is a Goalkeeper. This is another possible case.
The possible cases are presented in the following table:
Report a problem
Question for Practice Questions Level 1: Binary Logic
Try yourself:The player from Team-C plays at which position?
Explanation
Given that every player spoke exactly two false statements, hence they all spoke one true statement. Let the first statement of Stanley be true. Hence, the other two must be false. Therefore, Stanley is not playing for Team-A. Owen is not a mid-fielder and Geoffrey is not playing for Team-C.
Owen's second statement is, therefore, true. Hence, his first and third statements must be false, which means that Owen is not a defender and Stanley is not a mid-fielder. Owen has to be a goalkeeper. Stanley should be a defender. Geoffrey must be a mid-fielder.
Hence, Geoffrey's last statement is true. But Geoffrey's first statement is also true. Since this is not possible, Stanley's first statement cannot be true.
Let the second statement of Stanley be true. Therefore. Owen is a mid-fielder. From his other two statements, we can say that Stanley is from Team-A and Geoffrey is from the Team-B. Hence, Owen is from the Team-C. Owen's second statement is true. His first and third statements are false. Geoffrey's second statement is true. His first and third statements must be false. Therefore, Stanley must be a goalkeeper and Geoffrey must be a defender. This is one possible case.
Let Stanley's third statement be true. Geoffrey must be from Team-C. According to his first statement, Stanley must be from Team-A. Therefore, Owen must be from Team-B. Owen is not a mid-fielder.
Owen's second statement and Geoffrey's second statement are false. The only case possible in which both Owen and Geoffrey tell one true statement each is when Owen's first statement and Geoffrey's third statement are true. Hence, Owen is a defender, Geoffrey is a mid-fielder and Stanley is a goalkeeper. This is another possible case.
Report a problem
Question for Practice Questions Level 1: Binary Logic
Try yourself:Which team is Owen from?
Explanation
Given that every player spoke exactly two false statements, hence they all spoke one true statement. Let the first statement of Stanley be true. Hence, the other two must be false. Therefore, Stanley is not playing for Team-A. Owen is not a mid-fielder and Geoffrey is not playing for Team-C.
Owen's second statement is, therefore, true. Hence, his first and third statements must be false, which means that Owen is not a defender and Stanley is not a mid-fielder. Owen has to be a goalkeeper. Stanley should be a defender. Geoffrey must be a mid-fielder.
Hence, Geoffrey's last statement is true. But Geoffrey's first statement is also true. Since this is not possible, Stanley's first statement cannot be true.
Let the second statement of Stanley be true. Therefore. Owen is a mid-fielder. From his other two statements, we can say that Stanley is from Team-A and Geoffrey is from the Team-B. Hence, Owen is from the Team-C. Owen's second statement is true. His first and third statements are false. Geoffrey's second statement is true. His first and third statements must be false. Therefore, Stanley must be a goalkeeper and Geoffrey must be a defender. This is one possible case.
Let Stanley's third statement be true. Geoffrey must be from Team-C. According to his first statement, Stanley must be from Team-A. Therefore, Owen must be from Team-B. Owen is not a mid-fielder.
Owen's second statement and Geoffrey's second statement are false. The only case possible in which both Owen and Geoffrey tell one true statement each is when Owen's first statement and Geoffrey's third statement are true. Hence, Owen is a defender, Geoffrey is a mid-fielder and Stanley is a goalkeeper. This is another possible case.
The possible cases are presented in the following table:
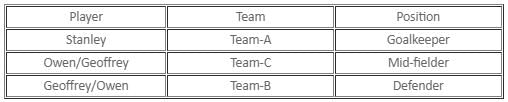
Hence, Owen can be from Team-C or Team-B, which means that it cannot be determined.
Report a problem
Question for Practice Questions Level 1: Binary Logic
Try yourself:Which of the following is true for the goalkeeper?
Explanation
Given that every player spoke exactly two false statements, hence they all spoke one true statement. Let the first statement of Stanley be true. Hence, the other two must be false. Therefore, Stanley is not playing for Team-A. Owen is not a mid-fielder and Geoffrey is not playing for Team-C.
Owen's second statement is, therefore, true. Hence, his first and third statements must be false, which means that Owen is not a defender and Stanley is not a mid-fielder. Owen has to be a goalkeeper. Stanley should be a defender. Geoffrey must be a mid-fielder.
Hence, Geoffrey's last statement is true. But Geoffrey's first statement is also true. Since this is not possible, Stanley's first statement cannot be true.
Let the second statement of Stanley be true. Therefore. Owen is a mid-fielder. From his other two statements, we can say that Stanley is from Team-A and Geoffrey is from the Team-B. Hence, Owen is from the Team-C. Owen's second statement is true. His first and third statements are false. Geoffrey's second statement is true. His first and third statements must be false. Therefore, Stanley must be a goalkeeper and Geoffrey must be a defender. This is one possible case.
Let Stanley's third statement be true. Geoffrey must be from Team-C. According to his first statement, Stanley must be from Team-A. Therefore, Owen must be from Team-B. Owen is not a mid-fielder.
Owen's second statement and Geoffrey's second statement are false. The only case possible in which both Owen and Geoffrey tell one true statement each is when Owen's first statement and Geoffrey's third statement are true. Hence, Owen is a defender, Geoffrey is a mid-fielder and Stanley is a goalkeeper. This is another possible case.
The possible cases are presented in the following table:
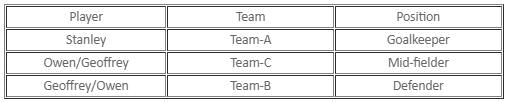
The name of the goalkeeper is Stanley.
Report a problem
Question for Practice Questions Level 1: Binary Logic
Try yourself:Which of the following statements is/are definitely true?
Explanation
Given that every player spoke exactly two false statements, hence they all spoke one true statement. Let the first statement of Stanley be true. Hence, the other two must be false. Therefore, Stanley is not playing for Team-A. Owen is not a mid-fielder and Geoffrey is not playing for Team-C.
Owen's second statement is, therefore, true. Hence, his first and third statements must be false, which means that Owen is not a defender and Stanley is not a mid-fielder. Owen has to be a goalkeeper. Stanley should be a defender. Geoffrey must be a mid-fielder.
Hence, Geoffrey's last statement is true. But Geoffrey's first statement is also true. Since this is not possible, Stanley's first statement cannot be true.
Let the second statement of Stanley be true. Therefore. Owen is a mid-fielder. From his other two statements, we can say that Stanley is from Team-A and Geoffrey is from the Team-B. Hence, Owen is from the Team-C. Owen's second statement is true. His first and third statements are false. Geoffrey's second statement is true. His first and third statements must be false. Therefore, Stanley must be a goalkeeper and Geoffrey must be a defender. This is one possible case.
Let Stanley's third statement be true. Geoffrey must be from Team-C. According to his first statement, Stanley must be from Team-A. Therefore, Owen must be from Team-B. Owen is not a mid-fielder.
Owen's second statement and Geoffrey's second statement are false. The only case possible in which both Owen and Geoffrey tell one true statement each is when Owen's first statement and Geoffrey's third statement are true. Hence, Owen is a defender, Geoffrey is a mid-fielder and Stanley is a goalkeeper. This is another possible case.
The possible cases are presented in the following table:
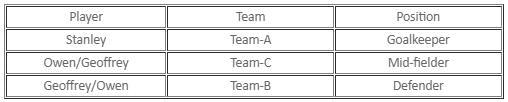
Hence, all are true.
Report a problem
Question for Practice Questions Level 1: Binary Logic
Try yourself:The person who supports Barcelona is
Explanation
After going through all statements made by Graeme, Harry, and Mathew, one can make out that Mathew's second statement is either a true statement of a truth-teller or a false statement of an alternator, irrespective of which Mathew's first and third statements have to be true. This gives us the following result:
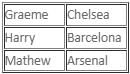
Based on above, we can determine that Graeme's first statement is false and second one is true. As the three of them have to be either a truth-teller, a liar, or an alternator, we can conclude that Graeme is an alternator and her third statement is hence false (which means Mathew is not an alternator). This leads us to the conclusion that Mathew is a truth-teller. Thus, Mathew's second statement can also be marked as true.
Hereafter, when we analyse Harry's statements, we realise that they all are false; so Harry must be a liar. With 'T' standing for true and 'F' for false, the nature of the statements will be as follows:
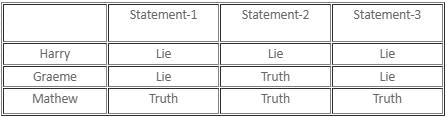
Hence, Harry supports Barcelona.
Report a problem
Question for Practice Questions Level 1: Binary Logic
Try yourself:Who among the following is a liar?
Explanation
After going through all statements made by Graeme, Harry, and Mathew, one can make out that Mathew's second statement is either a true statement of a truth-teller or a false statement of an alternator, irrespective of which Mathew's first and third statements have to be true. This gives us the following result:
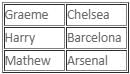
Based on above, we can determine that Graeme's first statement is false and second one is true. As the three of them have to be either a truth-teller, a liar, or an alternator, we can conclude that Graeme is an alternator and her third statement is hence false (which means Mathew is not an alternator). This leads us to the conclusion that Mathew is a truth-teller. Thus, Mathew's second statement can also be marked as true.
Hereafter, when we analyse Harry's statements, we realise that they all are false; so Harry must be a liar. With 'T' standing for true and 'F' for false, the nature of the statements will be as follows:
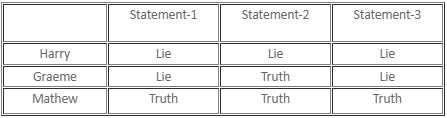
Harry is a liar.
Report a problem
Question for Practice Questions Level 1: Binary Logic
Try yourself:Which of the following statements is/are false?
Explanation
After going through all statements made by Graeme, Harry, and Mathew, one can make out that Mathew's second statement is either a true statement of a truth-teller or a false statement of an alternator, irrespective of which Mathew's first and third statements have to be true. This gives us the following result:

Based on above, we can determine that Graeme's first statement is false and second one is true. As the three of them have to be either a truth-teller, a liar, or an alternator, we can conclude that Graeme is an alternator and her third statement is hence false (which means Mathew is not an alternator). This leads us to the conclusion that Mathew is a truth-teller. Thus, Mathew's second statement can also be marked as true.
Hereafter, when we analyse Harry's statements, we realise that they all are false; so Harry must be a liar. With 'T' standing for true and 'F' for false, the nature of the statements will be as follows:
 All the above statements are false.
All the above statements are false.
Report a problem
Question for Practice Questions Level 1: Binary Logic
Try yourself:Who among the following supports Arsenal?
Explanation
After going through all statements made by Graeme, Harry, and Mathew, one can make out that Mathew's second statement is either a true statement of a truth-teller or a false statement of an alternator, irrespective of which Mathew's first and third statements have to be true. This gives us the following result:

Based on above, we can determine that Graeme's first statement is false and second one is true. As the three of them have to be either a truth-teller, a liar, or an alternator, we can conclude that Graeme is an alternator and her third statement is hence false (which means Mathew is not an alternator). This leads us to the conclusion that Mathew is a truth-teller. Thus, Mathew's second statement can also be marked as true.
Hereafter, when we analyse Harry's statements, we realise that they all are false; so Harry must be a liar. With 'T' standing for true and 'F' for false, the nature of the statements will be as follows:

Hence, Mathew supports Arsenal.
Report a problem