This EduRev document offers 20 Multiple Choice Questions (MCQs) from the topic Caselets (Level - 1). These questions are of Level - 1 difficulty and will assist you in the preparation of CAT & other MBA exams. You can practice/attempt these CAT Multiple Choice Questions (MCQs) and check the explanations for a better understanding of the topic.
Question for Practice Questions Level 1: Caselets - 2
Try yourself:Directions: Read the following information and answer the given question.
A doctor wanted to know the weight of 5 boys, each weighing less than 55 kg(Consider all the weights are natural numbers). The children would not let the doctor measure their weights on the weighing machine unless they were weighed in pairs. The weights (in kg) thus obtained were: 90, 92, 93, 94, 95, 96, 97, 98, 100 and 101. The names of the 5 children were Tinu, Minu, Chinu, Tipu and Tilu. Also, their weights were in the order Tilu > Tipu > Tinu > Minu > Chinu. The total weight of Tilu and Tipu is 101 kg, that of Minu and Chinu is 90 kg, and that of Tinu and Chinu is 92 kg.
Q. How many of them weighed less than 48 kg?
Explanation
Ranking of weights: Tilu > Tipu > Tinu > Minu > Chinu
Sum total of weights: Tilu + Tipu = 101 ... (1)
Sum total of weights: Minu + Chinu = 90 ... (2)
Sum total of weights: Tinu + Chinu = 92 ... (3)
Sum total of weights: 4(Tilu + Tipu + Tinu + Minu + Chinu) = 90 + 92 + 93 + 94 + 95 + 96 + 97 + 98 + 100 + 101
4(101 + Tinu + 90) = 956
Tinu = (956/4) - 191 = 48 kg
Hence, two people weighed less than 48 kg.
Report a problem
Question for Practice Questions Level 1: Caselets - 2
Try yourself:Directions: Read the following information and answer the given question.
A doctor wanted to know the weight of 5 boys, each weighing less than 55 kg(Consider all the weights are natural numbers). The children would not let the doctor measure their weights on the weighing machine unless they were weighed in pairs. The weights (in kg) thus obtained were: 90, 92, 93, 94, 95, 96, 97, 98, 100 and 101. The names of the 5 children were Tinu, Minu, Chinu, Tipu and Tilu. Also, their weights were in the order Tilu > Tipu > Tinu > Minu > Chinu. The total weight of Tilu and Tipu is 101 kg, that of Minu and Chinu is 90 kg, and that of Tinu and Chinu is 92 kg.
Q. What was the weight of Tinu?
Explanation
According to the question:
Ranking of weights: Tilu > Tipu > Tinu > Minu > Chinu
Sum total of weights: Tilu + Tipu = 101 kg
Sum total of weights: Minu + Chinu = 90 kg
Also, according to the question:
4(Tilu + Tipu + Tinu + Minu + Chinu) = 90 + 92 + 93 + 94 + 95 + 96 + 97 + 98 + 100 + 101
4(101 + Tinu + 90) = 956
Tinu = (956/4) - (101 + 90) = 48
Weight of Tinu = 48 kg
Report a problem
Question for Practice Questions Level 1: Caselets - 2
Try yourself:Directions: There are 300 students in the 2017-18 batch of MBA of IIM, Bangalore. Each student is either a boy or a girl, either doing a 'correspondence course' or a 'regular course' and is either an engineer or an accountant. The two Venn diagrams (below) give information about the number of students of the entire batch falling in different categories.
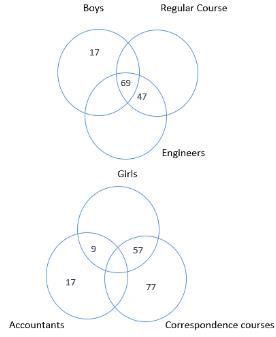
Q. Which of the following represents the lowest value?
1. Number of accountants who are doing a regular course
2. Number of boys who are accountants
3. Number of boys who are engineers and are doing a regular course
4. Number of accountants who are doing a correspondence course
Explanation

Option 1: Number of accountants who are doing a regular course = 17 + 9 = 26
Option 2: Number of boys who are accountants = 17 + 17 = 34
Option 3: Number of boys who are engineers and are doing a regular course = 69
Option 4: Number of accountants who are doing a correspondence course = 17 + 7 = 24
Report a problem
Question for Practice Questions Level 1: Caselets - 2
Try yourself:Directions: Read the information carefully to answer the question that follows.
Arun, Varun, Karun, Bhim and Shina had some red balls with them. When the teacher asked them about the number of red balls, one boy gave the following information.
1. The total number of red balls with all five boys is divisible by 2.
2. The number of balls with each boy had exactly 2 factors.
3. None of the boys had more than 28 balls.
4. No two boys had the same number of balls.
5. The total number of balls with any two of the given 5 boys is non-prime.
6. Varun had more red balls than twice the number of balls with Karun.
7. Karun had less red balls than balls with Bhim, while Varun had more red balls than balls with Arun.
8. The number of red balls with Bhim was less than one third of the number of red balls with Shina.
Q. What was the total sum of red balls with Bhim and Varun?
Explanation
Since the number of balls with each boy had exactly 2 factors, none of the boys had more than 28 balls and no two boys had same number of balls, so we have 2, 3, 5, 7, 11, 13, 17, 19 and 23 as options.
Since the total number of red balls with all five boys is divisible by 2, so one of them has 2 red balls.
Also, the total number of balls with any two of the given 5 boys is non-prime.
Now,
2 + 3 = 5 (Prime)
2 + 5 = 7 (Prime)
2 + 11 = 13 (Prime)
2 + 17 = 19 (Prime)
So, no boy had 3, 5, 11 and 17 balls.
Now, we have 2, 7, 13, 19 and 23 as options.
Now, the following is given.
Varun had more red balls than twice the balls with Karun.
The number of red balls with Bhim was less than one third the number of red balls with Shina.
Karun had less red balls than balls with Bhim.
The only condition which satisfies all the above conditions is Karun and Bhim having 2 and 7 balls.
So, Shina had 23 balls and since Varun had more balls than balls with Arun, so both of them have 19 and 13 balls each.
Required sum = 7 + 19 = 26
Report a problem
Question for Practice Questions Level 1: Caselets - 2
Try yourself:Directions: Read the information carefully to answer the question that follows.
Arun, Varun, Karun, Bhim and Shina had some red balls with them. When the teacher asked them about the number of red balls, one boy gave the following information.
1. The total number of red balls with all five boys is divisible by 2.
2. The number of balls with each boy had exactly 2 factors.
3. None of the boys had more than 28 balls.
4. No two boys had the same number of balls.
5. The total number of balls with any two of the given 5 boys is non-prime.
6. Varun had more red balls than twice the number of balls with Karun.
7. Karun had less red balls than balls with Bhim, while Varun had more red balls than balls with Arun.
8. The number of red balls with Bhim was less than one third of the number of red balls with Shina.
Q. For how many pairs was the sum of red balls a perfect square?
Explanation
Since the number of balls with each boy had exactly 2 factors, none of the boys had more than 28 balls and no two boys had same number of balls, so we have 2, 3, 5, 7, 11, 13, 17, 19 and 23 as options.
Since the total number of red balls with all five boys is divisible by 2, so one of them has 2 red balls.
Also, the total number of balls with any two of the given 5 boys is non-prime.
Now,
2 + 3 = 5 (Prime)
2 + 5 = 7 (Prime)
2 + 11 = 13 (Prime)
2 + 17 = 19 (Prime)
So, no boy had 3, 5, 11 and 17 balls.
Now, we have 2, 7, 13, 19 and 23 as options.
Now, the following is given.
Varun had more red balls than twice the balls with Karun.
The number of red balls with Bhim was less than one third the number of red balls with Shina.
Karun had less red balls than balls with Bhim.
The only condition which satisfies all the above conditions is Karun and Bhim having 2 and 7 balls.
So, Shina had 23 balls and since Varun had more balls than balls with Arun, so both of them have 19 and 13 balls each.
2 + 7 = 9
2 + 23 = 25
13 + 23 = 36
For 3 pairs, sum was a perfect square.
Report a problem
Question for Practice Questions Level 1: Caselets - 2
Try yourself:Directions: Read the information carefully to answer the question that follows.
Out of Raja, Deepak and Uday, one person was to be selected for the managing director's position. It was decided that all the employees of the company, excluding the candidates, will vote for them. Each employee could vote for a minimum of one and maximum of all three candidates. After the voting, the following was observed.
1. The difference between the number of employees who voted only for Raja and number of employees who voted for Deepak, but not for Uday, was zero.
2. 28 employees voted for only 2 contestants, while 19 employees voted for all 3 contestants.
3. If we subtract the number of employees who voted for Raja, but not for Deepak from the number of employees who voted for at least 2 contestants, we get 20 as the answer.
4. The number of employees who voted for both Deepak and Uday was 33, while the number of employees who voted for Uday, but not for Raja was 12 more than the number of employees who voted for all three contestants.
5. The number of employees who voted for Deepak was the same as the number of employees who voted of at least two contestants.
Q. How many employees voted for both Raja and Uday, but not for Deepak?
Explanation
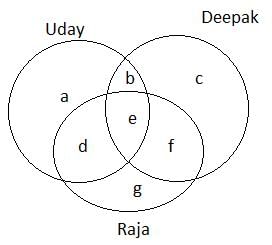
According to given condition,
g - (c + f) = 0
g = c + f ...(1)
b + d + f = 28 ...(2)
e = 19 ...(3)
g + d = e + b + d + f - 20 ...(4)
b + e + f - g = 20
33 - c = 20
c = 13
b + e = 33 ...(5)
a + b = 31 ...(6)
b = 14
a = 17
b + c + e + f = b + d + e + f ...(7)
c = d
Solving, we get
Required number = 13
Report a problem
Question for Practice Questions Level 1: Caselets - 2
Try yourself:Directions: Read the information carefully to answer the question that follows.
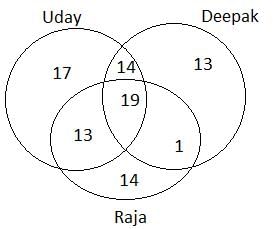
Out of Raja, Deepak and Uday, one person was to be selected for the managing director's position. It was decided that all the employees of the company, excluding the candidates, will vote for them. Each employee could vote for a minimum of one and maximum of all three candidates. After the voting, the following was observed.
1. The difference between the number of employees who voted only for Raja and number of employees who voted for Deepak, but not for Uday, was zero.
2. 28 employees voted for only 2 contestants, while 19 employees voted for all 3 contestants.
3. If we subtract the number of employees who voted for Raja, but not for Deepak from the number of employees who voted for at least 2 contestants, we get 20 as the answer.
4. The number of employees who voted for both Deepak and Uday was 33, while the number of employees who voted for Uday, but not for Raja was 12 more than the number of employees who voted for all three contestants.
5. The number of employees who voted for Deepak was the same as the number of employees who voted of at least two contestants.
Explanation
:

According to given condition,
g - (c + f) = 0
g = c + f … (1)
b + d + f = 28 … (2)
e = 19 ……(3)
g + d = e + b + d + f - 20 = 27 …..(4)
b + e = 33 ….(5)
a + b = 31 …..(6)
b + c + e + f = 47 …(7)
Solving, we get

Required number = 13 + 19 = 32
Report a problem
Question for Practice Questions Level 1: Caselets - 2
Try yourself:Directions: The question is based on the following table and information.
1. In 1984-85, the value of exports of manufactured articles exceeds the value of exports of raw materials by 100%.
2. In 1985-86, the ratio of % of exports of raw material to that of exports of manufactured articles is 3 : 4.
3. Exports of food in 1985-86 exceeds the 1984-85 figure by Rs. 1006 crore.
Percentage of Total Value of Exports in India
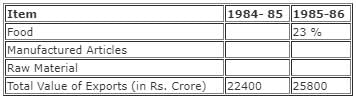
Q. The change in value of exports of manufactured articles from 1984-85 to 1985-86 is
Explanation
Value of food exports in 1985-86 = 0.23 × Rs. 25,800 crore = Rs. 5934 crore
Let the value of exports of raw material be 3y and that of manufactured articles be 4y.
So, 7y + Rs. 5934 crore = Rs. 25,800 crore
Or, y = Rs. 2838 crore
Thus, value of exports of manufactured articles in 1985-86 = 4 × Rs. 2838 crore = Rs. 11,352 crore
Value of food exports in 1984-85 = Rs. 5934 crore - Rs. 1006 crore = Rs. 4928 crore
Now, let the value of raw material exports in 1984-85 be z.
Thus, value of exports of manufactured articles in 1984-1985 be 2z.
Now, Rs. 4928 crore + 3z = Rs. 22,400 crore
Or, z = Rs. 5824 crore
Value of exports of manufactured articles in 1984-85 = 2z = 2 × Rs. 5824 crore = Rs. 11,648 crore
Thus, required value = Rs. (11648 - 11352) crore = Rs. 296 crore
Hence, option 1 is correct.
Report a problem
Question for Practice Questions Level 1: Caselets - 2
Try yourself:Directions: The question is based on the following table and information.
1. In 1984-85, the value of exports of manufactured articles exceeds the value of exports of raw materials by 100%.
2. In 1985-86, the ratio of % of exports of raw material to that of exports of manufactured articles is 3 : 4.
3. Exports of food in 1985-86 exceeds the 1984-85 figure by Rs. 1006 crore.
Percentage of Total Value of Exports in India

Q. During 1984-85, how much more raw material was exported as compared to food in terms of value?
Explanation
Food related exports in (1984-85) = food related exports in (1985-86) - Rs. 1006 crore = Rs. 0.23 × 25,800 crore - Rs. 1006 crore = Rs. 4928 crore
In 1984-85, exports of raw materials + exports of manufactured goods = Rs. (22400 - 4928) crore = Rs. 17,472 crore
And exports in manufactured goods = 2 × (exports of raw materials)
Exports of raw materials in 1984-85 = Rs. (17472/3) crore = Rs. 5824 crore
Difference between exports of raw materials and food exports = Rs. (5824 - 4928) crore = Rs. 896 crore
Hence, option (2) is correct.
Report a problem
Question for Practice Questions Level 1: Caselets - 2
Try yourself:Directions: Read the information carefully to answer the question that follows.
The premises of a school are to be renovated. The renovation is in terms of flooring. Certain areas are to be floored either with marble or wood. All classrooms/halls and pantry are rectangular. The area to be renovated comprises of a big hall measuring 25 m × 25 m, principal's room measuring 13 m × 17 m, a pantry measuring 14 m × 13 m, a recordkeeping cum server room measuring 21 m × 13 m and locker area measuring 29 m × 21 m. The total area of the school is 2000 square metres. The cost of wooden flooring is Rs. 100 per square metre and the cost of marble flooring is Rs. 150 per square metre. The locker area, recordkeeping cum server room and pantry are to be floored with marble. The principal's room and the hall are to be floored with wood. No other area is to be renovated in terms of flooring.
Q. As per given information, how much money will be spent on marble?
Explanation
Area to be floored with marble = Area of Pantry + Area of Recordkeeping cum server room + Area of Locker = (14 × 13) + (21 × 13) + (29 × 21) = 1064 m2
Total cost of renovation (Marble) = 1064 × 150 = Rs. 1,59,600
Report a problem
Question for Practice Questions Level 1: Caselets - 2
Try yourself:Directions: Read the information carefully to answer the question that follows.
The premises of a school are to be renovated. The renovation is in terms of flooring. Certain areas are to be floored either with marble or wood. All classrooms/halls and pantry are rectangular. The area to be renovated comprises of a big hall measuring 25 m × 25 m, principal's room measuring 13 m × 17 m, a pantry measuring 14 m × 13 m, a recordkeeping cum server room measuring 21 m × 13 m and locker area measuring 29 m × 21 m. The total area of the school is 2000 square metres. The cost of wooden flooring is Rs. 100 per square metre and the cost of marble flooring is Rs. 150 per square metre. The locker area, recordkeeping cum server room and pantry are to be floored with marble. The principal's room and the hall are to be floored with wood. No other area is to be renovated in terms of flooring.
Q. If the remaining area of the school is to be carpeted at a rate of Rs. 110/- per square metre, then how much will be the increment in the total cost of renovation of school premises?
Explanation
Total Area = 2000 m2
Total Area renovated with Marble and Wood = Area of Hall + Area of Principal's room + Area of Pantry + Area of Recordkeeping cum server room + Area of Locker = (25 × 25) + (13 × 17) + (14 × 13) + (21 × 13) + (29 × 21) = 1910 m2
Total Area to be carpeted = (2000 - 1910) m2 = 90 m2
Total cost of carpeting the remaining area = Rs. 90 × 110 = Rs. 9900
Report a problem
Question for Practice Questions Level 1: Caselets - 2
Try yourself:Directions: Study the given information and answer the following question.
A contractor built a residential colony where he constructed total 250 flats, which were of 3 types - 1 BHK, 2 BHK and 3 BHK. He offered these flats only to freedom fighters (FF), international level sportspersons (SP) and people below poverty line (PL).
In 1 BHK type flats, the ratio of persons who bought flats was 4 : 7 : 19 for FF : SP : PL. The total number of 1 BHK flats was 20 more than that of 3 BHK flats.
In 2 BHK type flats, the number of SP persons was 25% more than FF persons. The number of PL persons was 125% more than FF persons.
In 3 BHK type flats, the probability of selecting 1 PL person was 12/35. The number of FF and that of PL persons were the same. The total number of 3 BHK flats was more than 50 and less than 90.
Q. If we have to select 3 persons from the whole lot, what is the approximate probability that we get 1 from each group, i.e. 1 FF, 1 SP and 1 PL?
Explanation
Let m be the total number of 3 BHK flats. Hence, total 1 BHK flats = m + 20
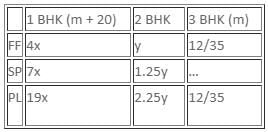
1 BHK (m + 20)2 BHK 3 BHK (m)FF4xy12/35SP7x1.25y…PL19x2.25y12/35
Let's first take 3 BHK. We know, P (PL) = 12/35 and total number of flats is between 50 and 90. So, the denominator should be a multiple of 35. Only 70 is between 50 and 90.
Hence, total 3 BHK flats = 70
Total PL flats in 3 BHK = 12 × 2 = 24
Total FF flats in 3 BHK = 24
Total SP flats in 3 BHK = 70 – 24 – 24 = 22
So, total 1 BHK flats = 70 + 20 = 90
We know, FF : SP : PL in 1 BHK is 4 : 17 : 19
Hence,
Total FF flats in 1 BHK = 90 × 4/30 = 12
Total SP flats in 1 BHK = 90 × 7/30 = 21
Total PL flats in 1 BHK = 90 × 19/30 = 57
Total flats = 250
So, total 2 BHK flats = 250 – 90 – 70 = 90, which are in ratio 1 : 1.25 : 2.25
Total FF flats in 2 BHK = 90 × 1/4.5 = 20
Total SP flats in 2 BHK = 90 × 1.25/4.5 = 25
Total PL flats in 2 BHK = 90 × 2.25/4.5 = 45
After putting all conditions, we get
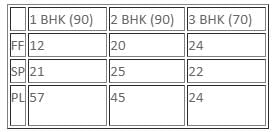
1 BHK (90)2 BHK (90)3 BHK (70)FF122024SP212522PL574524
Total FF = 12 + 20 + 24 = 56
Total SP = 21 + 25 + 22 = 68
Total PL = 57 + 45 + 24 = 126
Required probability = 56/250 × 68/249 × 126/248 = 0.03
Report a problem
Question for Practice Questions Level 1: Caselets - 2
Try yourself:Directions: Study the given information carefully and answer the following question.
3 groups A, B and C from a school went for a picnic. In each group, there were boys, girls and teachers.
In group A, number of boys is 3 more than that of girls. If we have to select one member from this group, then the probability of him being a teacher is 4/11.
In group B, number of girls is 50% more than that of boys. If 2 persons are selected from group B at random, then probability of both being teachers is 1/136. Total number of persons in group B is 17.
In group C, the ratio of teachers to boys is 1 : 3 and that of teachers to girls is 1 : 4. Total number of persons in this group is 48.
Q. The difference between the number of boys in group C and that in group B is what percent more/less than the sum of the numbers of teachers in groups A and B?
Explanation
Group A:
B = G + 3
Probability (T) = 4/11
Let's assume there are total 11 members and number of teachers is 4. It means B = 5 and G = 2.
Group B:
Total = 17
G = 1.5B
Let's assume T = 1, then B + G should be 16 but we can't have an integral value from G = 1.5B that will satisfy B + G = 16.
Let T = 2, then B + G = 17 - 2 = 15. From G = 1.5B, we get G = 9, B = 6.
Probability of 2 teachers = 2/17 × 1/16 = 1/136, which is given. Hence, it's correct.
Group C:
T : B = 1 : 3
T : G = 1 : 4
It means T : G : B = 3 : 12 : 9
But total = 48, hence T = 6, G = 24, B = 18
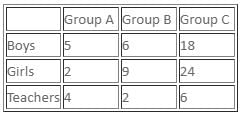
Difference between the number of boys in group C and that in group B = 18 - 6 = 12
Number of teachers in group A and B together = 4 + 2 = 6
∴ Required % = ((12-6)/6) × 100 = 100%
Report a problem
Question for Practice Questions Level 1: Caselets - 2
Try yourself:Directions: Study the given information carefully and answer the following question.
3 groups A, B and C from a school went for a picnic. In each group, there were boys, girls and teachers.
In group A, number of boys is 3 more than that of girls. If we have to select one member from this group, then the probability of him being a teacher is 4/11.
In group B, number of girls is 50% more than that of boys. If 2 persons are selected from group B at random, then probability of both being teachers is 1/136. Total number of persons in group B is 17.
In group C, the ratio of teachers to boys is 1 : 3 and that of teachers to girls is 1 : 4. Total number of persons in this group is 48.
Q. x boys from group B go to group A and 50% of teachers from group A go to group B. If one person is selected at random from group B and probability of him being a teacher is 1/4, then what is the value of x?
Explanation
Group A:
B = G + 3
Probability (T) = 4/11
Let's assume there are total 11 members, and the number of teachers is 4. It means B = 5 and G = 2.
Group B:
Total = 17
G = 1.5B
Let's assume T = 1, then B + G should be 16 but we can't have integral value from G = 1.5B that will satisfy B + G = 16.
Let T = 2, then B + G = 17 - 2 = 15. From G = 1.5B, we get G = 9, B = 6.
Probability of 2 teachers = 2/17 × 1/16 = 1/136, which is given. Hence, it's correct.
Group C:
T : B = 1 : 3
T : G = 1 : 4
It means T : G : B = 1 : 4 : 3
But total = 48, hence T = 6, G = 24, B = 18
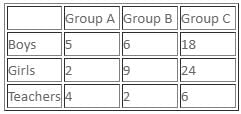
After:

It is clear that 2 teachers from group A go to group B.
Now, teachers in Group B = 4
P(T) = 1/4 (Given)
Hence, total members in group B will be 16.
It means number of boys = 3.
Hence, x = 3 boys from group B go to group A.
Report a problem
Question for Practice Questions Level 1: Caselets - 2
Try yourself:A survey of 170 families, 115 drink Coffee, 110 drink Tea and 130 drink Milk. Also, 85 drink Coffee and Milk, 75 drink Coffee and Tea, 95 drink Tea and Milk, 70 drink all the three. Find How many use Coffee and Milk but not Tea.
Explanation
Given,
Number of families who participate in survey = 170
Number of families who drink Coffee = 115
Number of families who drink Tea = 110
Number of families who drink Milk = 130
Number of families who drink Coffee and Milk = 85
Number of families who drink Coffee and Tea = 75
Number of families who drink Tea and Milk = 95
Number of families who drink Coffee, Milk and Tea = 70
Calculation:
Number of families who drink only Milk and Tea = 95 – 70 = 25
Number of families who drink only Coffee and Milk = 85 – 70 = 15
Report a problem
Question for Practice Questions Level 1: Caselets - 2
Try yourself:200 students appeared in a specific examination.
There were 80 students who failed in Mathematics.
160 students passed in Physics.
30 students failed in Chemistry.
30 students failed in Mathematics and Physics.
15 students failed in Mathematics and Chemistry.
10 students failed in Physics and Chemistry.
100 students passed in all three subjects.
Q. How many students failed in only one subject?
Explanation
Concept used:
The Venn diagram is constructed based on the number of students who failed the exam.
Calculation:
From the given information we get,
C + D + G + F = 30
G + E = 30
G + F = 15
D + G = 10
B + E + G + F = 80
From the data we can deduce the following:
A + E + G + D = 200 - 160 = 40
C + A + D = 20
A + E + B = 70
B + F + C = 60
Substituting and solving we get,
A = 5, B = 40, E = 25, G = 5, F = 10, C = 10, D = 5
Number of people who failed in only one subject = A + B + C = 5 + 40 + 10 = 55
Report a problem
Question for Practice Questions Level 1: Caselets - 2
Try yourself:Direction: Read the information carefully and answer the following questions:
In a school of 750 students, each student likes atleast one of the three colors- Red, Green and Blue. 109 students like only red color, 150 students like only green color and 125 students like only blue color. The number of students who like red and green colors only is 70% of the students who like only green color. The number of students who like red and blue colors only is 60% of the students who like only blue color. 100 students like all the colors.
Q. What is the difference between the number of students who like only one color and the number of students who like only two colors?
Explanation
Total number of students = 750

The number of students who like red and green colors only = 70% of 150 students
and The number of students who like red and blue colors only = 60% of 125 students
Calculation:
Let the number of students who like green and blue colors only be a.
Number of students who like red and green colors only = (70/100) × 150
⇒ 105 students
Number of students who like red and blue colors only = (60/100) × 125
⇒ 75 students
Then, The total number of students = 750
⇒ 109 + 150 + 125 + 100 + 105 + 75 + a = 750
⇒ 664 + a = 750
⇒ a = 750 – 664
⇒ a = 86 students
Now, The number of students who like only one color = 109 + 150 + 125
⇒ 384 students
and The number of students who like only two colors = 105 + 75 + 86
⇒ 266 students
Required difference = 384 – 266
⇒ 118
∴ 118 is the difference between the number of students who like only one color and the number of students who like only two colors.
Report a problem
Question for Practice Questions Level 1: Caselets - 2
Try yourself:Direction: Read the following information carefully and answer the following questions
In a school consisting of 700 students, a sports event is organized. There are a total of 4 sports i.e Baseball, Cricket, Hockey and Basketball. Each student participated in one sport.
i) Ratio between the number of boys and girls who participated in Cricket is 11 ∶ 13 and that of Hockey is 15 ∶ 13.
(ii) The number of girls who participated in baseball is 20 less than the number of boys and the number of boys who participated in cricket is 35 more than the number of boys who participated in Hockey.
(iii) The ratio between the number of boys and girls who participated in Basketball is 5 ∶ 3
(iv) The ratio of the number of girls and boys who participated in baseball is 7 ∶ 9 and the difference between the number of boys and girls who participated in cricket is 20.
Q. The number of boys who participated in baseball and cricket together is what percentage of number of girls who participated in the same sports?
Explanation
Common explanation:
Ratio between the number of boys and girls who participated in Cricket is 11 ∶ 13 and the difference between the number of boys and girls who participated in cricket is 20
∴ Let the number of boys and girls who participated in cricket be 11x and 13x respectively
⇒ 13x – 11x = 20
⇒ 2x = 20
⇒ x = 10
∴ Number of boys who participated in cricket = 11 × 10 = 110
Number of girls who participated in cricket = 13 × 10 = 130
Ratio between the number of boys and girls who participated in Hockey is 15 ∶ 13 and the number of boys who participated in cricket is 35 more than the number of boys who participated in Hockey.
Let the number of boys and girls who participated in Hockey be 15x and 13x respectively
∴ Number of boys who participated in Hockey = 110 – 35 = 75
⇒ 15x = 75
⇒ x = 5
∴ Number of girls who participated in Hockey = 13 × 5 = 65
The ratio of the number of girls and boys who participated in baseball is 7 ∶ 9 and the number of girls who participated in baseball is 20 less than the number of boys
∴ Let the number of boys and girls who participated in baseball be 9x and 7x respectively
⇒ 9x – 7x = 20
⇒ 2x = 20
⇒ x = 10
∴ Number of boys who participated in baseball = 9 × 10 = 90
Number of girls who participated in baseball = 7 × 10 = 70
Now, the students who took part in Basketball known that there are 700 students in the school
⇒ 700 – (110 + 130 + 75 + 65 + 90 + 70) = 700 – 540 = 160
The ratio between the number of boys and girls who participated in Basketball is 5 ∶ 3
∴ Let the number of boys and girls who participated in basketball be 5x and 3x respectively
⇒ 5x + 3x = 160
⇒ 8x = 160
⇒ x = 20
∴ Number of boys who participated in basketball = 5 × 20 = 100
Number of girls who participated in basketball = 3 × 20 = 60
Following table can be prepared from the above data:
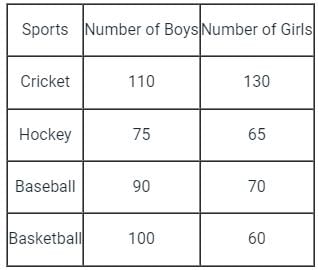 Solution:
Solution:
From the above table:
Total number of boys who participated in baseball and cricket = 90 + 110 = 200
Total number of boys who participated in baseball and cricket = 130 + 70 = 200
∴ Required percentage = (200/200) × 100 = 100%
∴ The number of boys who participated in baseball and cricket together is 100% of number of girls who participated in the same sports.
Report a problem
Question for Practice Questions Level 1: Caselets - 2
Try yourself:Directions: Based on the given passage, answer the questions that follow.
A invested Rs. 50000 in a company in the beginning of the year. After few months, B invested Rs. 40000 in the same company. At the end of the year, A received Rs. 12000 as his share of profit for the year. In the next year, A and B again invested the same amount as they did in the previous year for the whole year. After 3 months, C invested Rs. 60000 and received Rs. 4500 as his share of profit at the end of second year.
Q. In the third year, if A, B and C invested the same amount as before in the second of the year, what is C’s share in a profit of Rs. 60000?
Explanation
In third year,
A’s investment = Rs. 50000 for 12 months
B’s investment = Rs. 40000 for 12 months
C’s investment = Rs. 60000 for 12 months
Hence,
⇒ A’s share : B’s share : C’s share = 50000 : 40000 : 60000
⇒ A’s share : B’s share : C’s share = 5 : 4 : 6
∴ C’s share = (6/15) × 60000 = Rs. 24000
Report a problem
Question for Practice Questions Level 1: Caselets - 2
Try yourself:Direction: Read the following information carefully and answer the following questions.
A class has a total of 500 students. All the students are involved in exactly one of three different activities, i.e. Dancing, Singing, and Photography. The number of students in dancing is 20% of total students in the class and the ratio of boys to girls in dancing is 3: 7. The number of students in photography is 60% of the number of students in singing. The number of girls in Singing is 50 less than the number of boys in Singing. The number of girls in photography is 87.5% of the number of boys in Photography.
Q. Find the number of students involved in Photography.
Explanation
Calculation:
The total number of students is 500.
Students involved in dancing is 20% of the total students.
⇒ 20% of 500 = 100 students
Let the students involved in photography be P, those in dancing be D and students involved in singing be S.
⇒ P + S + D = 500 ----(1)
⇒ P + S = 500 - D
⇒ P + S = 400 ----(2)
It is given that students involved in photography is 60% of students involved in singing
⇒ P = 60 % of S ----(3)
put the value of P = 60 S/100 in equation (2)
⇒ 60 S /100 + S = 400
⇒ 16 S/10 = 400
⇒ S = 250
⇒ From equation (2) ,
⇒ P + S = 400
⇒ P + 250 = 400
⇒ P = 150
∴ Number of students involved in photography is 15
Report a problem













 Solution:
Solution:

















