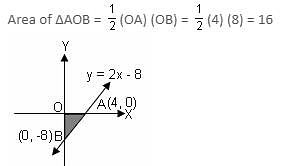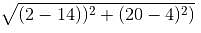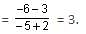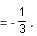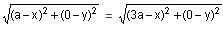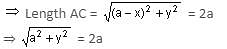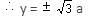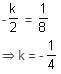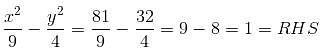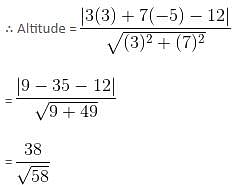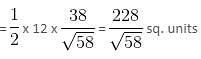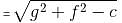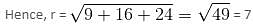This EduRev document offers 15 Multiple Choice Questions (MCQs) from the topic Coordinate Geometry (Level - 1). These questions are of Level - 1 difficulty and will assist you in the preparation of CAT & other MBA exams. You can practice/attempt these CAT Multiple Choice Questions (MCQs) and check the explanations for a better understanding of the topic.
Question for Practice Questions Level 1: Coordinate Geometry
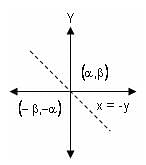
Try yourself:The image of the point (α, β) in the line x + y = 0 is
Explanation
P (α, β) lies in the 1st quadrant. Image of point (α, β) in the line x + y = 0 lies in IIIrd quadrant, i.e. (- β, - α)

Report a problem
Question for Practice Questions Level 1: Coordinate Geometry
Try yourself:In the diagram, the line with equation y = 2x - 8 crosses x-axis at A and y-axis at B. The area of ΔAOB is

Explanation
Point B is the y-intercept of y = 2x - 8, and so has coordinates (0, - 8).
Point A is the x-intercept of y = 2x - 8, so we set y = 0 and obtain 0 = 2x - 8
⇒ 2x = 8
⇒ x = 4
A has coordinates (4, 0).

Report a problem
Question for Practice Questions Level 1: Coordinate Geometry
Try yourself:If x-form (x, y) = (x2 + x, y2 - y) and y-form (x, y) = (x2 - 11 , y2) are two functions defined on a plane, then find the distance between the points x-form (-2, 5) and y-form (5, -2)
Explanation
x-form (x, y) = (x2 + x, y2 - y); For (-2, 5), coordinates of A are (2 , 20).
y-form (x, y) = (x2 - 11, y2); For (-5, 2), co-ordinates of B are (14, 4).
Distance between A and B is


AB = 20 units
Report a problem
Question for Practice Questions Level 1: Coordinate Geometry
Try yourself:Find the equation of the straight line passing through the point (-2, -3) and perpendicular to the line passing through (-2, 3) and (-5, -6).
Explanation
Report a problem
Question for Practice Questions Level 1: Coordinate Geometry
Try yourself:The lines a1x + b1y + c1 = 0 and a2x + b2y + c2 = 0 are perpendicular to each other if
Explanation
b1y = -a1x - c1
b2y = -a2x - c2
Slope of line 1 (m1) = -a1/b1
Slope of line 2 (m2) = -a2/b2
For lines to be perpendicular, m1m2 = -1
(-a1/b1)(-a2/b2) = -1
a1a2 = -b1b2
a1a2 + b1b2 = 0
Report a problem
Question for Practice Questions Level 1: Coordinate Geometry
Try yourself:Find the coordinates of the point which divides P1(1, -4) and P2(4, 2) externally in the ratio 1 : 4.
Explanation
Let P(X, Y) be the point which divides P1(1, -4) and P2(4, 2) externally in the ratio 1 : 4.
By section formula, X = {1 + (-1/4)(4)}/(1 - ¼) = 0
Y = {-4 + (-1/4) (2)}/(1 - ¼) = -6
Report a problem
Question for Practice Questions Level 1: Coordinate Geometry
Try yourself:The vertices of a triangle are at (0, 0), (8, 0) and (0, 14). The orthocentre of the triangle is at
Explanation
If the vertices of the triangle are at A(8, 0), B(0, 14) and O(0, 0), then [OA] ⊥ [OB]; hence, altitudes through A and B meet at O.
So, the orthocentre of the triangle is at (0, 0).
Report a problem
Question for Practice Questions Level 1: Coordinate Geometry
Try yourself:If A (a, 0) and B (3a, 0) are the vertices of an equilateral triangle ABC, then what are the coordinates of C?
Explanation
Report a problem
Question for Practice Questions Level 1: Coordinate Geometry
Try yourself:The equation of the straight line which passes through the point (3, 4) and makes an intercept on the y-axis twice as long as that on the x-axis is
Explanation
Let x-intercept = a and y-intercept = 2a
Using intercept form, we get
Equation of line,
(x/a) + (y/2a) = 1
2x + y = 2a
As it passes through a point (3, 4), therefore,
2(3) + 4 = 2a
a = 5
So, the required equation of line is 2x + y = 10.
Report a problem
Question for Practice Questions Level 1: Coordinate Geometry
Try yourself:The value of k for which the circles x2 + y2 - 3x + ky - 5 = 0 and 4x2 + 4y2 - 12x - y - 9 = 0 become concentric is
Explanation
Since the circles are concentric, so their centres will be the same.
The centre of circle x2 + y2 - 3x + ky - 5 = 0 is (3/2, -k/2).
The centre of circle 4x2 + 4y2 - 12x - y - 9 = 0 is (3/2, 1/8).
This implies,

Report a problem
Question for Practice Questions Level 1: Coordinate Geometry
Try yourself:What is the equation of a straight line which passes through the point of intersection of the straight lines x – 3y + 1 = 0 and 2x + 5y – 9 = 0 and has infinite slope?
Explanation
x – 3y + 1 = 0
⇒ 2x – 6y + 2 = 0 ... (i)
2x + 5y – 9 = 0 ... (ii)
(i) - (ii) gives:
-6y - 5y + 2 + 9 = 0
y = 1
Substitute the value of y in equation (i), we get
x = 2
So, the intersection point of x – 3y + 1 = 0 and 2x + 5y – 9 = 0 is (2, 1) and m = 1/0 (because the slope is infinite).
So, the required line is (y – 1) = (1/0)(x – 2), which gives x - 2 = 0 or x = 2.
Report a problem
Question for Practice Questions Level 1: Coordinate Geometry
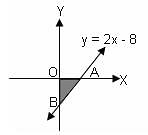
Try yourself:The curve  passes through the point
passes through the point
Explanation
On checking the options one by one, we get that only option (4) satisfies the given curve.
Putting x = 9 and y = 4√2, we get

Thus, option 4 is correct.
Report a problem
Question for Practice Questions Level 1: Coordinate Geometry
Try yourself:A triangle has 12 units base on the line 3x + 7y = 12. If the third vertex is at point (3, - 5), find the area of the triangle.
Explanation
The perpendicular distance of the vertex (3, -5) from the line is the altitude of the triangle.

Required area of triangle

Report a problem
Question for Practice Questions Level 1: Coordinate Geometry
Try yourself:The area of the circle x2 + y2 - 6x - 8y - 24 = 0 is
Explanation
Equation of a circle = x2 + y2 + 2gx + 2fy + c = 0
where r = radius of the circle 
Comparing with the given equation, g = -3, f = -4, c = -24

Area of a circle = πr2 = 49π sq. units
Report a problem
Question for Practice Questions Level 1: Coordinate Geometry
Try yourself:If u = a1x + b1y + c1 = 0, v = a2x + b2y + c2 and a1/a2 = b1/b2 = c1/c2 , then locus of the equation u + λv = 0, λ ∈ R is
Explanation
Since a1/a2 = b1/b2 = c1/c2 , = μ (say), therefore the straight lines u = 0 and v = 0 are coincident.
Also, u + λv = 0.
⇔ a1x + b1y + c1 + λ(a2x + b2y + c2) = 0
⇔ μ(a2x + b2y + c2) + λ(a2x + b2y + c2) = 0
⇔ (μ + λ)(a2x + b2y + c2) = 0
⇔ (μ + λ) v = 0
So, v = 0
Similarly, u = 0
Report a problem
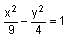 passes through the point
passes through the point