This EduRev document offers 10 Multiple Choice Questions (MCQs) from the topic Exponents & Logarithm (Level - 1). These questions are of Level - 1 difficulty and will assist you in the preparation of CAT & other MBA exams. You can practice/attempt these CAT Multiple Choice Questions (MCQs) and check the explanations for a better understanding of the topic.
Question for Practice Questions Level 1: Exponents & Logarithm
Try yourself:If log 3 = 0.47712, what will be the number of digits in 364?
Explanation
log 3 = 0.47712 …. (1)
log (364) = 64 x log 3
= 64 x 0.47712 (from equation1)
= 30.53568
Its characteristic is 30.
Hence, the number of digits in 364 is (30 + 1) = 31
Option (3) is correct.
Report a problem
Question for Practice Questions Level 1: Exponents & Logarithm
Try yourself:Solve the following equation for x:
log10 x - log10 √x = = 2 logx 10
Explanation
log10 x - 1/2 log10 x = 2 logx 10 ...(I)
or, 1/2 log10 x = 2 logx 10 ...(II)
Using base change rule (logb a = 1/loga b), equation (II) becomes:
1/2 log10 x = 2/log10 x
(log10 x)2 = 4
or, log10 x = ±2
x = 100 or x = 1/100
Report a problem
Question for Practice Questions Level 1: Exponents & Logarithm
Try yourself:Find the value of 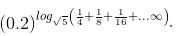
Explanation
Report a problem
Question for Practice Questions Level 1: Exponents & Logarithm
Try yourself:If pa = qb = rc and 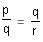 , then
, then 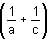 b =
b =
Explanation
Report a problem
Question for Practice Questions Level 1: Exponents & Logarithm
Try yourself:If 3x = 4y = 12z, find the value of z.
Explanation
3 = 12z/x ... (1)
4 = 12z/y ... (2)
Multiply (1) and (2);
12 = 12(z/x) + (z/y)

Report a problem
Question for Practice Questions Level 1: Exponents & Logarithm
Try yourself:The value of log4 3 × log5 4 x … x log9 8 × log3 9 is _______.
Explanation
log4 3 × log5 4 x … x log9 8 × log3 9
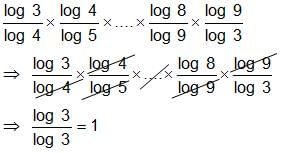
Report a problem
Question for Practice Questions Level 1: Exponents & Logarithm
Try yourself:Find a and b, if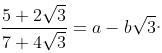
Explanation

(Comparing this with a - b √3 : a = 11, b = 6)
Report a problem
Question for Practice Questions Level 1: Exponents & Logarithm
Try yourself:If the values of log10 2, log10 3 and log10 7 are known, which one of the following cannot be evaluated?
Explanation
- log10 75 = log10 (3 x 52) = log10 3 + 2log10 5
- log10 252 = log10 (22 x 32 x 7) = 2 log10 2 + 2log10 3 + log10 7
- log10 98 = log10 (72 x 2) = 2 log10 7 + log10 2
- All of the above can be easily solved, but log10 770 (log10 7 x log10 11) cannot be solved because log10 11 is unknown.
- Hence, option (d) is correct.
Report a problem
Question for Practice Questions Level 1: Exponents & Logarithm
Try yourself:The possible values of x for the equation log2 x2 + logx 2 = 3 are
Explanation
log2 x2 + logx 2 = 3
⇒ 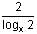 + logx 2 = 3
+ logx 2 = 3
⇒ 2 + (logx 2)2 - 3 logx 2 = 0
Put y = logx 2
⇒ y2 - 3y + 2 = 0
⇒ y = 1, 2
For y = 1, logx 2 = 1 or x = 2
For y = 2, logx 2 = 2 or x = √2
Hence, there are two valid values of x, i.e. x = 2, √2.
Report a problem
Question for Practice Questions Level 1: Exponents & Logarithm
Try yourself:A sequence is given by log7 2, log7 4, log7 16, log7 256, ........... The common ratio of this geometric progression is
Explanation
Given sequence can be written as follows.
log7 2, log7 22, log7 24, log7 28, ……….
It can be further written as
log7 2, 2 log7 2, 4 log7 2, 8 log7 2, ………. [log mn = n log m]
By dividing 2nd term by 1st term, we get common ratio, r = 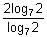 = 2
= 2
Report a problem
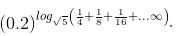
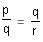 , then
, then 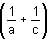 b =
b =
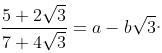

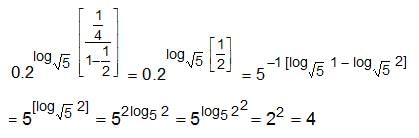

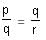
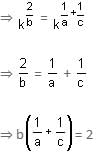

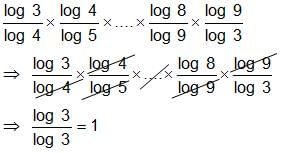

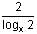 + logx 2 = 3
+ logx 2 = 3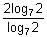 = 2
= 2



















