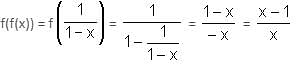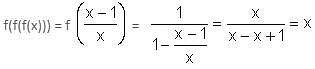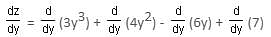This EduRev document offers 20 Multiple Choice Questions (MCQs) from the topic Functions (Level - 1). These questions are of Level - 1 difficulty and will assist you in the preparation of CAT & other MBA exams. You can practice/attempt these CAT Multiple Choice Questions (MCQs) and check the explanations for a better understanding of the topic.
Question for Practice Questions Level 1: Functions - 2
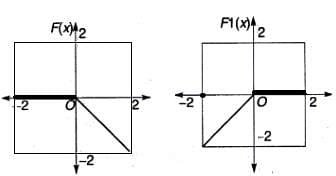
Try yourself:Directions: Answer the question based on the following information.
A function has been defined for a variable x, where domain of F(x) and F1(x) ∈ [-2, 2].

Choose the correct option.
Explanation
F(2) = -2 and F1(-2) = -2
F(-2) = 0 and F1(2) = 0
So, according to this,
F(x) = F1(-x) or F1(x) = F(-x)
Report a problem
Question for Practice Questions Level 1: Functions - 2
Try yourself:If f(x) = x3 + y3, g(x) = xy and h(x) = (x + y), then which of the following is the value of f(x)?
Explanation
x3 + y3 = (x + y)3 - 3xy (x + y)
= (x + y) [(x + y)2 - 3xy]
= h(x) [ {h(x)}2 - 3g(x) ]
Report a problem
Question for Practice Questions Level 1: Functions - 2
Try yourself:An exponential function is given by f(x) = a3x. If the point  lies on the graph of this function, then the value of 'a' is
lies on the graph of this function, then the value of 'a' is
Explanation
Given function is f(x) = a3x
As point  lies on the given curve, it must satisfy the given equation.
lies on the given curve, it must satisfy the given equation.

a = 7
Report a problem
Question for Practice Questions Level 1: Functions - 2
Try yourself:If f : R - {3} → R - {1} is defined by f(x) =  , then f is
, then f is
Explanation
Here, y = f(x)

Which is defined for y ∈ R - {1}
Hence f(x) is invertible.
∴ One - one and onto
Report a problem
Question for Practice Questions Level 1: Functions - 2
Try yourself:Which of the following options is necessarily true if f(x) = x3 - 4x + p and f(0) and f(1) have opposite signs?
Explanation
f(x) = x3 - 4x + p
f(0) = p
f(1) = 1 - 4 + p = p - 3
∵ f(0) and f(1) have opposite signs
∴ f(0) and f(1) < 0
p(p - 3) < 0
0 < p < 3
Report a problem
Question for Practice Questions Level 1: Functions - 2
Try yourself:If f(x) = ax2 + bx + c and c =  then the graph of y = f(x) will certainly
then the graph of y = f(x) will certainly
Explanation

This shows that root of equation are real and equal. Thus, the graph touches the x-axis and is hence tangential to the x-axis.
Thus, answer option 3 is correct.
Report a problem
Question for Practice Questions Level 1: Functions - 2
Try yourself:If f(x) = 3x - 5 and f(g(x)) = 2x, then g(x) equals
Explanation
Given: f(x) = 3x - 5 and f(g(x)) = 2(x)
f(g(x)) = 3g(x) - 5 = 2x
3g(x) - 5 = 2x
g(x) = (2x + 5)/3
Report a problem
Question for Practice Questions Level 1: Functions - 2
Try yourself:If f(a, b) = a2 + b3, g(a, b) = a + b, then what is the value of f(3, g(3, 4))?
Explanation
f(a, b) = a2 + b3
g(a, b) = a + b
g(3, 4) = 7
f(3, g(3, 4)) = f(3, 7) = 32 + 73 = 352
Report a problem
Question for Practice Questions Level 1: Functions - 2
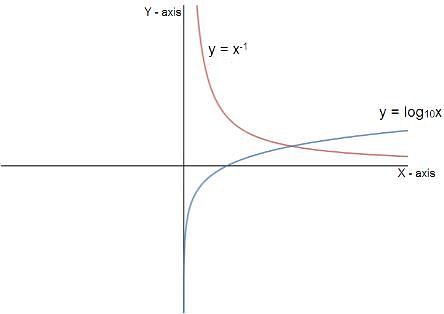
Try yourself:When the curves y = log10 x and y = x-1 are drawn in the x - y plane, how many times do they intersect for the values x ≥ 1?
Explanation
It is given that y = log10x & y = 1/x
Draw their graphs approximately and check.

Here, we see the graph has only 1 intersection point.
Report a problem
Question for Practice Questions Level 1: Functions - 2
Try yourself:Find the minimum value of x2 - 12x + 27.
Explanation
f (x) = x2 - 12x + 27 = x2 - 12x + 36 - 9
= (x - 6)2 - 9.
Since (x - 6)2 ≥ 0, the minimum value of the expression is - 9.
Report a problem
Question for Practice Questions Level 1: Functions - 2
Try yourself:A balloon, which always remains spherical, has a variable radius. Find the rate at which its volume is increasing with respect to its radius, when the radius is 7 cm.
Explanation
Let x be the radius and y be the volume of the balloon.
Then, y = 4/3πx3 dy/dx = 4πx2
 = 4π(7)2 = 196π cm2
= 4π(7)2 = 196π cm2
Hence, the volume is increasing with respect to its radius at the rate of 196 π cm2, when the radius is 7 cm.
Report a problem
Question for Practice Questions Level 1: Functions - 2
Try yourself:Find the two numbers such that their sum is 12 and the sum of their squares is minimum.
Explanation
Let the numbers be x and 12 - x.
∴ Sum of squares = x2 + (12 - x)2 = f(x), say.
∴ f` (x) = 2x + 2 (12 - x) (-1) = 4(x - 6)
∴ f`(x) = 0, only when x = 6.
The numbers are 6 and 6.
Report a problem
Question for Practice Questions Level 1: Functions - 2
Try yourself:The sum of two numbers is 2k. The numbers such that the sum of their squares is minimum, will be
Explanation
The sum of squares of two numbers is minimum when the numbers are equal.
Report a problem
Question for Practice Questions Level 1: Functions - 2
Try yourself:Refer to the following data to answer the question given below:
R(x, y) = and sq(x, y) =
and sq(x, y) = 
rem (x, y) = remainder when x is divided by y
q(x, y) = quotient when x is divided by y
sq(5, 10) is equal to
Explanation
sq(5, 10) =  [R(5, 10)]
[R(5, 10)]
Report a problem
Question for Practice Questions Level 1: Functions - 2
Try yourself:If f(x) =  then f[f[f(x)]] equals
then f[f[f(x)]] equals
Explanation
Report a problem
Question for Practice Questions Level 1: Functions - 2
Try yourself:Radius of a circle is increasing uniformly at the rate of 3 cm/sec. The rate of increase in area, when radius is 10 cm will be
Explanation
dr/dt = 3, we have A = πr2 ⇒ dA/dt = 2 π r (dr/dt)
⇒ (dA/dt)r = 10 = 2π x 10 x 3 = 60 π cm2/s
Report a problem
Question for Practice Questions Level 1: Functions - 2
Try yourself:Differentiate 3y3 + 4y2 - 6y + 7 w.r.t. y.
Explanation
Let z = 3y3 + 4y2 - 6y + 7
Differentiating both sides w.r.t. y,

= 9y2 + 8y - 6 + 0 = 9y2 + 8y - 6
Report a problem
Question for Practice Questions Level 1: Functions - 2
Try yourself:If f(x) is an even function, then the graph y = f(x) will be symmetrical about
Explanation
Report a problem
Question for Practice Questions Level 1: Functions - 2
Try yourself:If f (x) is an odd function, then the graph y = f(x) will be symmetrical about
Explanation
Report a problem
Question for Practice Questions Level 1: Functions - 2
Try yourself:Find the minimum value of the function f (x) = log2 (x2 – 2x + 5).
Explanation
The minimum value of the function would occur at the minimum value of (x2 – 2x + 5) as this quadratic function has imaginary roots.
For
y = x2 – 2x + 5
dy/dx = 2x – 2 = 0 ⇒ x = 1
⇒ x2 – 2x + 5 = 4.
Report a problem
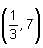 lies on the graph of this function, then the value of 'a' is
lies on the graph of this function, then the value of 'a' is
 , then f is
, then f is
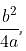 then the graph of y = f(x) will certainly
then the graph of y = f(x) will certainly
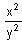 and sq(x, y) =
and sq(x, y) = 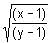
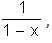 then f[f[f(x)]] equals
then f[f[f(x)]] equals


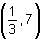 lies on the given curve, it must satisfy the given equation.
lies on the given curve, it must satisfy the given equation.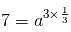
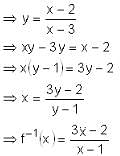
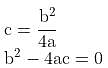
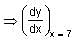 = 4π(7)2 = 196π cm2
= 4π(7)2 = 196π cm2 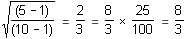 [R(5, 10)]
[R(5, 10)]