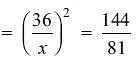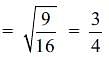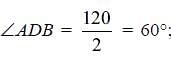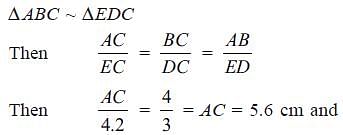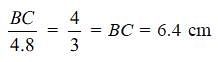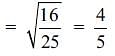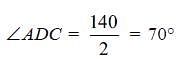This EduRev document offers 20 Multiple Choice Questions (MCQs) from the topic Geometry (Level - 1). These questions are of Level - 1 difficulty and will assist you in the preparation of CAT & other MBA exams. You can practice/attempt these CAT Multiple Choice Questions (MCQs) and check the explanations for a better understanding of the topic.
Question for Practice Questions Level 1: Geometry - 2
Try yourself:A vertical stick 20 m long casts a shadow 10 m long on the ground. At the same time, a tower casts the shadow 50 m long on the ground. Find the height of the tower.
Explanation
When the length of stick = 20 m, then length of shadow = 10 m i.e. in this case length = 2 x shadow.
With the same angle of inclination of the sun, the length of tower that casts a shadow of 50 m ⇒ 2 x 50 m = 100 m
i.e. height of tower = 100 m
Report a problem
Question for Practice Questions Level 1: Geometry - 2
Try yourself:The area of similar triangles, ABC and DEF are 144 cm2 and 81 cm2 respectively. If the longest side of larger ΔABC be 36 cm, then the longest side of smaller ΔDEF is
Explanation
For similar triangles fi (Ratio of sides)2 = Ratio of areas
Then as per question

{Let the longest side of ΔDEF = x}

Report a problem
Question for Practice Questions Level 1: Geometry - 2
Try yourself:The areas of two similar Ds are respectively 9 cm2 and 16 cm2. Find the ratio of their corresponding sides.
Explanation
Ratio of corresponding sides

Report a problem
Question for Practice Questions Level 1: Geometry - 2
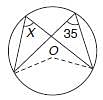
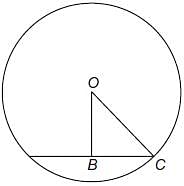
Try yourself:If O is the centre of circle, find ∠x

Explanation
∠x = 35°; because angles subtended by an arc, anywhere on the circumference are equal.
Report a problem
Question for Practice Questions Level 1: Geometry - 2
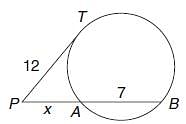
Try yourself:Find the value of x in the given figure.

Explanation
By the rule of tangents, we get
122 = (x + 7) x ⇒ 144 = x2 + 7x
⇒ x2 + 7x – 144 = 0
⇒ x2 + 16x – 9x – 144 = 0
⇒ x(x + 16) – 9(x + 16)
⇒ x = 9 or –16
–16 can’t be the length, hence this value is discarded, thus, x = 9
Report a problem
Question for Practice Questions Level 1: Geometry - 2
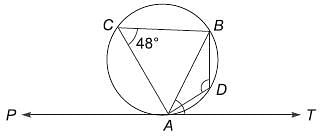
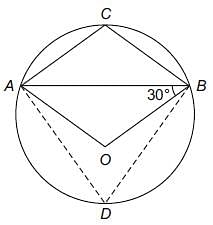
Try yourself:In the given figure, find ∠ADB.

Explanation
ADBC is a cyclic quadrilateral as all its four vertices are on the circumference of the circle. Also, the opposite angles of the cyclic quadrilateral are supplementary.
Therefore, ∠ADB = 180 – 48° = 132°
Report a problem
Question for Practice Questions Level 1: Geometry - 2
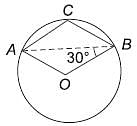
Try yourself:In the following figure, O is the centre of the circle and ∠ABO = 30°, find ∠ACB.

Explanation

OB = OA = radius of the circle
∠AOB = 180 – (30 + 30)
{Sum of angles of a triangle = 180°)
⇒ 120°
Then

because the angle subtended
by a chord at the centre is twice of what it
can subtend at the circumference. Again, ABCD is a cyclic quadrilateral;
So ∠ACB = 180° – 60° = 120° (because opposite angles of cyclic quadrilateral are supplementary).
Report a problem
Question for Practice Questions Level 1: Geometry - 2
Try yourself:In the figure, AB is parallel to CD and RD | | SL || TM || AN, and BR : RS : ST : TA = 3 : 5 : 2 : 7. If it is known that CN = 1.333 BR. Find the ratio of BF : FG : GH : HI : IC

Explanation
Since the lines AB and CD are parallel to each other, and the lines RD and AN are parallel, it means that the triangles RBF and NCI are similar to each other.
Since the ratio of CN:BR = 1.333, if we take BR as 3, we will get CN as 4. This means that the ratio of BF:CI would also be 3:4. Also, the ratio of BR:
RS:ST:TA = BF:FG:GH:HI = 3:5:2:7 (given). Hence, the correct answer is 3:5:2:7:4.
Report a problem
Question for Practice Questions Level 1: Geometry - 2
Try yourself:In the figure, DABC is similar to DEDC.

If we have AB = 4 cm,
ED = 3 cm, CE = 4.2 and
CD = 4.8 cm, find the value of CA and CB
Explanation
Report a problem
Question for Practice Questions Level 1: Geometry - 2
Try yourself:Two isosceles Ds have equal angles and their areas are in the ratio 16 : 25. Find the ratio of their corresponding heights.
Explanation
(Ratio of corresponding sides)2 = Ratio of area of similar triangles
∴ Ratio of corresponding sides in this question

Report a problem
Question for Practice Questions Level 1: Geometry - 2
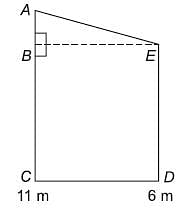
Try yourself:Two poles of height 6 m and 11 m stand vertically upright on a plane ground. If the distance between their foot is 12 m, find the distance between their tops.
Explanation

BC = ED = 6 m
So AB = AC – BC = 11 – 6 = 5 m
CD = BE = 12 m
Then by Pythagoras theorem:
AE2 = AB2 + BE2 ⇒ AE = 13 m
Report a problem
Question for Practice Questions Level 1: Geometry - 2
Try yourself:Find the length of a chord that is at a distance of 12 cm from the centre of a circle of radius 13 cm.
Explanation
In the DOBC, OB = 12 cm, OC = radius = 13 cm.
Then using Pythagoras theorem;
BC2 = OC2 – OB2 = 25; BC = 5 cm
Length of the chord = 2 x BC = 2 x 5 = 10 cm

Report a problem
Question for Practice Questions Level 1: Geometry - 2
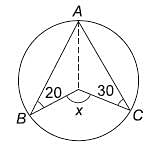
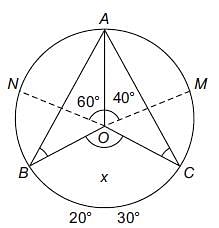
Try yourself:Find the value of ∠x in the given figure.

Explanation

∠AOM = 2∠ABM and
∠AON = 2∠ACN
because angle subtended by an arc at the centre of the circle is twice the angle subtended by it on the circumference on the same segment.
∠AON = 60° and ∠ AOM = 40°
∠X = ∠AON + ∠AOM
(∵ vertically opposite angles).
∠ X = 100°
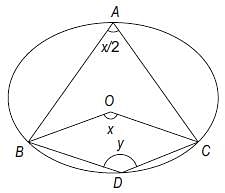
Alternately, you could also solve this using the following process:

In the given figure, join the points BD and CD. Then, in the cyclic quadrilateral ABDC, the sum of angles x/2 and y would be 180o. Hence, y = 180 – x/2. Also, the sum of the angles OBD + OCD = 180 – 20 - 30
= 130°. Therefore, x + y = 230 (as the sum of the angles of the quadrilateral OBDC is 360). Solving, the two equations, we get x = 100.
Report a problem
Question for Practice Questions Level 1: Geometry - 2
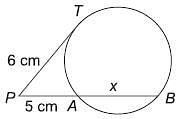
Try yourself:Find the value of x in the given figure.

Explanation
By the rule of tangents, we know:
62 = (5 + x)5 ⇒ 36 = 25 + 5x ⇒ 11 = 5x ⇒ x = 2.2 cm
Report a problem
Question for Practice Questions Level 1: Geometry - 2
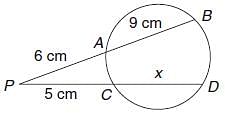
Try yourself:Find the value of x in the given figure.

Explanation
By the rule of chords, cutting externally, we get
⇒ (9 + 6)6 = (5 + x)5 ⇒ 90 = 25 + 5x ⇒ 5x = 65
⇒ x = 13 cm
Report a problem
Question for Practice Questions Level 1: Geometry - 2
Try yourself:In the given figure AB is the diameter of the circle and ∠PAB = 25°. Find ∠TPA.

Explanation
∠APB = 90° (angle in a semicircle = 90°)
∠PBA = 180 – (90 + 25) = 65°
∠TPA = ∠PBA (the angle that a chord makes
with the tangent, is subtended by the chord on the circumference in the alternate segment).
= 65°
Note: This is also called as the Alternate Segment Theorem.
Report a problem
Question for Practice Questions Level 1: Geometry - 2
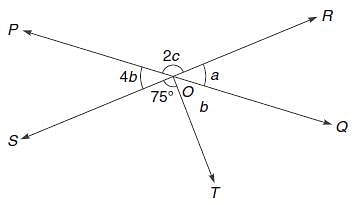
Try yourself:In the given figure, two straight lines PQ and RS intersect each other at O. If ∠SOT = 75°, find the value of a, b and c.

Explanation
From the given figure we have:
4b + 2c = 180 (1)
a + b = 105 (2)
4b = a (3)
Solving these equations, we get that b = 21°; a = 84°; c = 48°.
Report a problem
Question for Practice Questions Level 1: Geometry - 2
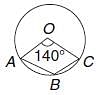
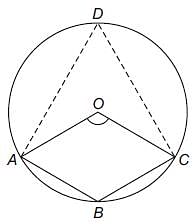
Try yourself:In the following figure, it is given that o is the centre of the circle and ∠AOC = 140°. Find ∠ABC.

Explanation


(because the angle subtended
by an arc on the circumference is half of what it subtends at the centre). ABCD one cyclic quadrilateral
So ∠ABC = 180° – 70° = 110° (because opposite.angles of a cyclic quadrilateral are supplementary).
Report a problem
Question for Practice Questions Level 1: Geometry - 2
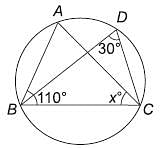
Try yourself:In the following figure, find the value of x

Explanation
∠BAC = 30° (∵ angles subtended by an arc anywhere on the circumference in the same segment are equal).
In DBAC; ∠x = 180° – (110° + 30°) = 40°
(∵ sum of angles of a triangle = 180°)
Report a problem
Question for Practice Questions Level 1: Geometry - 2
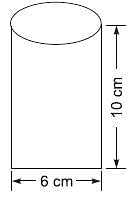
Try yourself:Find the perimeter of the given figure.

Explanation
Perimeter of the figure = 10 + 10 + 6 + 6π = 26 + 6π
Report a problem