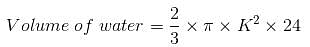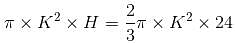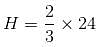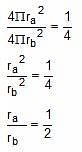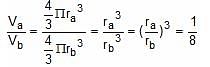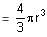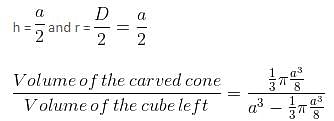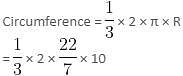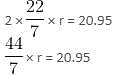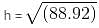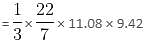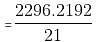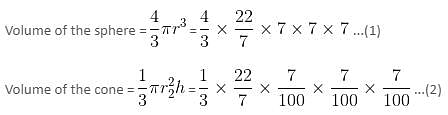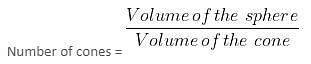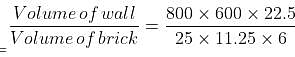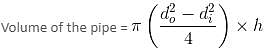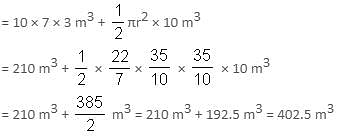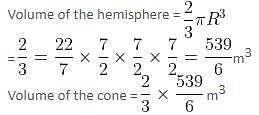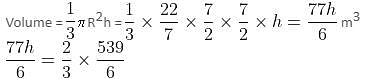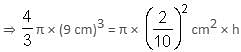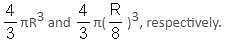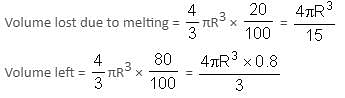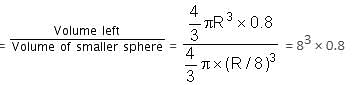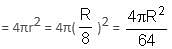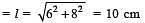This EduRev document offers 20 Multiple Choice Questions (MCQs) from the topic Mensuration (Level - 1). These questions are of Level - 1 difficulty and will assist you in the preparation of CAT & other MBA exams. You can practice/attempt these CAT Multiple Choice Questions (MCQs) and check the explanations for a better understanding of the topic.
Question for Practice Questions Level 1: Mensuration - 2
Try yourself:A right circular cone of radius K cm and height 24 cm rests on the base of a right circular cylinder of radius K cm (their bases lie in the same plane, as shown in the figure). The cylinder is filled with water to a height of 24 cm. If the cone is then removed, to which height will the water fall?

Explanation
Report a problem
Question for Practice Questions Level 1: Mensuration - 2
Try yourself:The curved surface areas of two spheres are in the ratio of 1 : 4. Find the ratio of their volumes.
Explanation
Let the two spheres be A and B.


Report a problem
Question for Practice Questions Level 1: Mensuration - 2
Try yourself:The ratio of the volume of a sphere to its surface area is
Explanation
Volume of a sphere

Surface area = 4πr2

Ratio of the volume to the surface area = r : 3
Report a problem
Question for Practice Questions Level 1: Mensuration - 2
Try yourself:A right-circular cone is carved out of a cube having the same height and radius, equal to half the side of the cube. What is the ratio of the volume of the carved cone to that of the cube left after carving?
Explanation
Given height and diameter:


Report a problem
Question for Practice Questions Level 1: Mensuration - 2
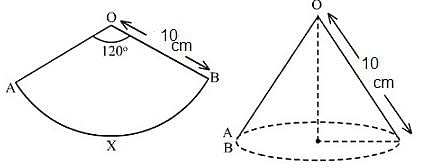
Try yourself:The sector of a circle with radius 10 cm and angle 120° is rolled up such that the two bounding radii are joined together to form a cone. Find the volume of the cone.
Explanation
Report a problem
Question for Practice Questions Level 1: Mensuration - 2
Try yourself:A sphere is melted and recast into smaller right cones of height 7 centimeters and radius 7 centimeters. If the radius of the sphere is 7 meters, then how many cones can be made?
Explanation
Radius of the sphere, r = 7 meters
Radius of the cone, r2 = 7 centimeters = 0.07 meters
Height of the cone, h = 7 centimeters = 0.07 meters


Solving,
Number of cones = 4 × 106
Report a problem
Question for Practice Questions Level 1: Mensuration - 2
Try yourself:Water flows at a rate of 10 m per minute from a cylindrical pipe, 5 mm in diameter. How long will it take to fill up a conical vessel whose diameter of the base is 40 cm and depth is 24 cm?
Explanation
Volume of the conical vessel = (1/3) × π × (20)2 × 24 = 3200π cm3
Volume flown in 1 minute = (π × (2.5/10)2 × 1000) = 62.5π cm3
Therefore, time taken = 3200π/62.5π = 51 min 12 sec
Report a problem
Question for Practice Questions Level 1: Mensuration - 2
Try yourself:A wall 8 m long, 6 m high and 22.5 cm thick is made up of bricks, each measuring 25 cm × 11.25 cm × 6 cm. Find the number of bricks required.
Explanation
Number of bricks required

= 6400
Report a problem
Question for Practice Questions Level 1: Mensuration - 2
Try yourself:A piece of metal pipe is 7 cm long with inner diameter of the cross section as 4 cm. If the outer diameter is 4.5 cm and the metal weighs 8 gm/cu cm, the weight of the pipe is
Explanation
Report a problem
Question for Practice Questions Level 1: Mensuration - 2
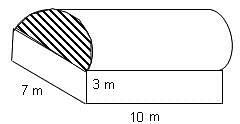
Try yourself:A building is in the form of a cuboid mounted by a semi-circular portion as shown. The inner measurements of the cuboid are 10 m × 7 m × 3 m and the radius of semi-circular portion is 3.5 m. Find the volume of the building.

Explanation
Radius of semi-circle = 3.5 m
Volume of the building = Volume of cubical portion + Volume of vertical cross-section

Report a problem
Question for Practice Questions Level 1: Mensuration - 2
Try yourself:A toy is made in the form of a hemisphere surmounted by a right circular cone whose circular base coincides with the plane surface of the hemisphere. The base radius of the cone is 3.5 m and its volume is (2/3)rd of the volume of the hemisphere. Calculate its height.
Explanation
Radius of the hemisphere = Base radius of the cone = 3.5 m

Let the height of the cone be h metres.

⇒ h = 4.67 m
Report a problem
Question for Practice Questions Level 1: Mensuration - 2
Try yourself:A sphere of diameter 18 cm made up of copper is melted and converted into a wire of diameter 4 mm. Find the length of the wire (in metres).
Explanation
Volume of the sphere = Volume of the wire (cylinder)

⇒ h = 24,300 cm = 243 metres
Report a problem
Question for Practice Questions Level 1: Mensuration - 2
Try yourself:A solid metal sphere is melted and smaller spheres, all with the same radius, are formed. 20% of the material is lost in this process. The radius of each smaller sphere is 1/8 the radius of the original sphere. If 20 litres of paint was needed to paint the original sphere, then how many litres of paint would be required to paint all the smaller spheres?
Explanation
Report a problem
Question for Practice Questions Level 1: Mensuration - 2
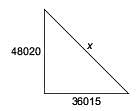
Try yourself:In a right angled triangle, find the hypotenuse if base and perpendicular are respectively 36015 cm and 48020 cm.
Explanation

Let hypotenuse = x cm
Then, by Pythagoras theorem:
x2 = (48020)2 + (36015)2
x ⇒ 60025 cm
Report a problem
Question for Practice Questions Level 1: Mensuration - 2
Try yourself:The inner circumference of a circular track is 440 cm. The track is 14 cm wide. Find the diameter of the outer circle of the track.
Explanation
Let inner radius = r; then 2π r = 440
∴ r = 70
Radius of outer circle = 70 + 14 = 84 cm ∴ Outer diameter = 2 × Radius = 2 × 84 = 168
Report a problem
Question for Practice Questions Level 1: Mensuration - 2
Try yourself:The outer circumference of a circular track is 220 meter. The track is 7 meter wide everywhere. Calculate the cost of levelling the track at the rate of 50 paise per square meter.
Explanation
Let outer radius = R; then inner radius = r = R – 7
2πR = 220 ⇒ R = 35 m;
r = 35 – 7 = 28 m
Area of track = π R2 – πr2 ⇒ p(R2 – r2)
= 1386 m2
Report a problem
Question for Practice Questions Level 1: Mensuration - 2
Try yourself:A pit 7.5 meter long, 6 meter wide and 1.5 meter deep is dug in a field. Find the volume of soil removed in cubic meters.
Explanation
Volume of soil removed = l × b × h = 7.5 × 6 × 1.5 = 67.5 m3
Report a problem
Question for Practice Questions Level 1: Mensuration - 2
Try yourself:The length, breadth and height of a room are in the ratio of 3 : 2 : 1. If its volume be 1296 m3, find its breadth
Explanation
Let the common ratio be = x
Then; length = 3x, breadth = 2x and height = x
Then; as per question 3x · 2x · x = 1296 ⇒ 6x3 = 1296
⇒ x = 6 m
Breadth = 2x = 12 m
Report a problem
Question for Practice Questions Level 1: Mensuration - 2
Try yourself:The whole surface of a rectangular block is 8788 square cm. If length, breadth and height are in the ratio of 4 : 3 : 2, find length.
Explanation
Let the common ratio be = x
Then, length = 4x, breadth = 3x and height = 2x
As per question;
2(4x · 3x + 3x · 2x + 2x · 4x) = 8788
2(12x2 + 6x2 + 8x2) = 8788 ⇒ 52x2 = 8788
⇒ x = 13 Length = 4x = 52 cm
Report a problem
Question for Practice Questions Level 1: Mensuration - 2
Try yourself:Find curved and total surface area of a conical flask of radius 6 cm and height 8 cm.
Explanation
Slant length 
Then curved surface area = πrl = π × 6 × 10⇒ 60p
And total surface area = πrl + πr2 ⇒ π ((6 × 10) + 62)
= 96π cm2
Report a problem