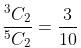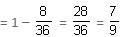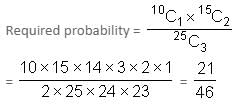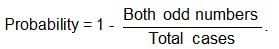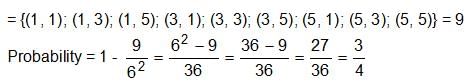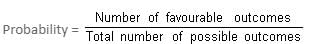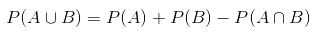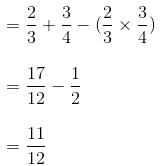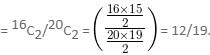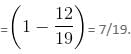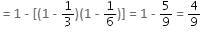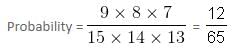This EduRev document offers 20 Multiple Choice Questions (MCQs) from the topic Probability (Level - 1). These questions are of Level - 1 difficulty and will assist you in the preparation of CAT & other MBA exams. You can practice/attempt these CAT Multiple Choice Questions (MCQs) and check the explanations for a better understanding of the topic.
Question for Practice Questions Level 1: Probability - 2
Try yourself:What are the odds against drawing 2 red balls from a bag containing 3 red and 2 white balls?
Explanation
Probability of selecting two red balls = 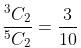
Odds in favour = 3 : 7
Odds against = 7 : 3
Report a problem
Question for Practice Questions Level 1: Probability - 2
Try yourself:Three unbiased coins are tossed. What is the probability of getting at most two tails?
Explanation
S = {TTT, TTH, THT, HTT, THH, HTH, HHT, HHH }.
E = {HHT, HTH, THH, HTT, THT, TTH, HHH}.
Therefore, P(E) = 7/8
Report a problem
Question for Practice Questions Level 1: Probability - 2
Try yourself:In a single throw of two dice, find the probability that neither a doublet nor a total of 10 will appear.
Explanation
Total outcomes = 36
Favourable outcomes for getting a doublet or a total of 10 = [(1, 1), (2, 2), (3, 3), (4, 4), (5, 5), (6, 6), (4, 6), (6, 4)]
Probability = 8/36
Probability that neither a doublet nor a total of 10 will appear
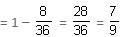
Hence, answer option 1 is correct.
Report a problem
Question for Practice Questions Level 1: Probability - 2
Try yourself:The number lock of a suitcase has 4 wheels, each labelled with ten digits, i.e. from 0 to 9. The lock opens with a sequence of four digits with no repeats. What is the probability of a person getting the sequence to open the suitcase?
Explanation
There are 10C4 × 4! = 5040 sequences of 4 distinct digits, out of which there is only one sequence in which the lock opens.
Required probability = 1/5040
Report a problem
Question for Practice Questions Level 1: Probability - 2
Try yourself:Three dice are rolled together. What is the probability of getting the same number on the three?
Explanation
Total number of possible cases = 63 = 216
Favourable number of cases = 6
Probability = 6/216 = 1/36
Report a problem
Question for Practice Questions Level 1: Probability - 2
Try yourself:In a class, there are 15 boys and 10 girls. Three students are selected at random. Find the probability that 1 girl and 2 boys are selected.
Explanation
Number of ways of choosing 1 girl out of 10 = 10C1
Number of ways of choosing 2 boys out of 15 = 15C2
Total number of ways of choosing 3 students out of 25 (15 + 10) = 25C3
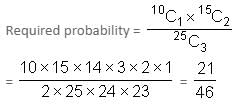
Report a problem
Question for Practice Questions Level 1: Probability - 2
Try yourself:Two dice are thrown. Find the probability that the product of two numbers received is even.
Explanation
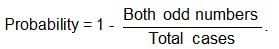
Total cases = 62
Both odd numbers
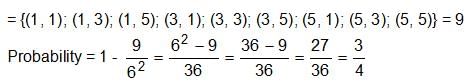
Report a problem
Question for Practice Questions Level 1: Probability - 2
Try yourself:A biased coin is tossed 700 times. Heads appears 300 times and tails appears 400 times. If the coin is tossed again, the probability of getting heads is
Explanation
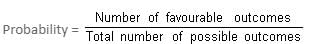
Number of favourable outcomes = 300, as heads has appeared 300 times.
Total number of possible outcomes = 700, as the coin is tossed 700 times.
⇒ Probability = 300/700 = 3/7
Report a problem
Question for Practice Questions Level 1: Probability - 2
Try yourself:The probability that A can solve a problem is 2/3 and the probability that B can solve the problem is 3/4. The probability that at least one of A and B will be able to solve the problem is
Explanation
Probability that at least one of A and B will solve the problem
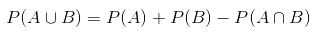
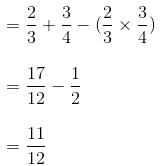
Report a problem
Question for Practice Questions Level 1: Probability - 2
Try yourself:There are 20 pens in a bag. 4 pens are defective. Two pens are chosen at random from the bag. The probability that at least one of these is defective is
Explanation
P(None is defective)
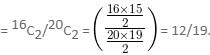
P(at least one is defective)
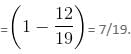
Report a problem
Question for Practice Questions Level 1: Probability - 2
Try yourself:The chances of winning of two race horses are 1/3 and 1/6. What is the probability that at least one will win, if the horses are running in different races?
Explanation
Probability that at least one horse will win = 1 - Probability that neither horse will win
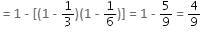
Report a problem
Question for Practice Questions Level 1: Probability - 2
Try yourself:What is the probability of getting a sum of 6 from two throws of a dice?
Explanation
S = Sample space = 36.
E = Event of getting the sum as 6.
Favorable outcomes = {(2,4), (4,2), (1,5), (5,1), (3,3)}.
So, n(E) = 5.
P(E) = 5/36.
Report a problem
Question for Practice Questions Level 1: Probability - 2
Try yourself:A coin is tossed five times. Find the probability of getting 2 heads and 3 tails.
Explanation
Total number of cases when a coin is flipped five times = 32
Favourable number of cases (2 heads and 3 tails) = 5C2 or 5C3 = 10
Required probability = 10/32 = 5/16
Report a problem
Question for Practice Questions Level 1: Probability - 2
Try yourself:A bag contains 6 white and 9 black balls. If three balls are drawn at random, then find the probability that all of them are black.
Explanation
Total number of outcomes = 15C3
Number of favourable outcomes = 9C3
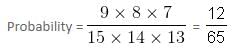
Report a problem
Question for Practice Questions Level 1: Probability - 2
Try yourself:Two dice are rolled simultaneously. Find the probability of getting a multiple of 2 on one die and a multiple of 3 on the other die.
Explanation
E = {(2, 3), (2, 6), (4, 3), (4, 6), (6, 3), (6, 6), (3, 2), (3, 4), (3, 6), (6, 2), (6, 4)}
n(E) = 11
n(s) = 36
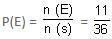
Report a problem
Question for Practice Questions Level 1: Probability - 2
Try yourself:The letters of the word 'LEADING' are placed at random in a row. What is the probability that three vowels come together?
Explanation
Total number of sample spaces = 7!
Total number of favourable outcomes = 3! × 5!
Required probability = (3! × 5!)/7!
= 1/7
Report a problem
Question for Practice Questions Level 1: Probability - 2
Try yourself:The probability that in a group of 3 people, at least two will have the same birthday is
Explanation
Let A be the event that at least two people have the same birthday.
Then,

Report a problem
Question for Practice Questions Level 1: Probability - 2
Try yourself:In throwing a fair dice, what is the probability of getting the number ‘3’?
Explanation
Out of a total of 6 occurrences, 3 is one possibility = 1/6.
Report a problem
Question for Practice Questions Level 1: Probability - 2
Try yourself:Find the chance of throwing at least one ace in a simple throw with two dice.
Explanation
Event definition is:
(1 and 1) or (1 and 2) or (1 and 3) or (1 and 4) or
(1 and 5) or (1 and 6) or (2 and 1) or (3 and 1) or
(4 and 1) or (5 and 1) or (6 and 1)
Total 11 out of 36 possibilities = 11/36
Report a problem
Question for Practice Questions Level 1: Probability - 2
Try yourself:From a pack of 52 cards, two are drawn at random. Find the chance that one is a knave and the other a queen.
Explanation
Knave and queen or Queen and Knave → 4/52 × 4/51 + 4/52 × 4/51 = 8/663
Report a problem