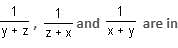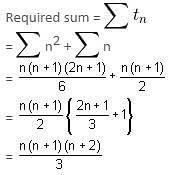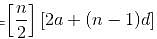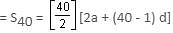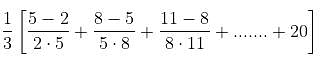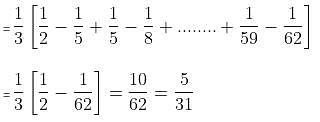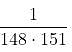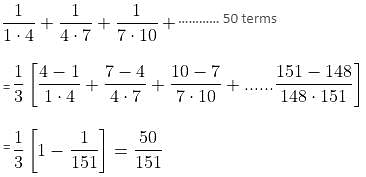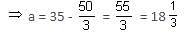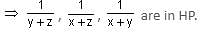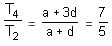This EduRev document offers 10 Multiple Choice Questions (MCQs) from the topic Progressions, Sequences & Series (Level - 1). These questions are of Level - 1 difficulty and will assist you in the preparation of CAT & other MBA exams. You can practice/attempt these CAT Multiple Choice Questions (MCQs) and check the explanations for a better understanding of the topic.
Question for Practice Questions Level 1: Progressions, Sequences & Series - 1
Try yourself:Find the value of 12 + 1 + 22 + 2 + 32 + 3 + ... + n2 + n.
Explanation
The nth term of the given series is tn = n2 + n, n = 1, 2, 3, ..., n

Report a problem
Question for Practice Questions Level 1: Progressions, Sequences & Series - 1
Try yourself:Susan had arranged to pay off her debt of $3,600 to CASA Bank in 40 monthly installments in the form of an A.P. When 30 of the installments had been repaid, she died leaving one third of the debt unpaid. What was the value of the first installment?
Explanation
Report a problem
Question for Practice Questions Level 1: Progressions, Sequences & Series - 1
Try yourself:
Explanation
Report a problem
Question for Practice Questions Level 1: Progressions, Sequences & Series - 1
Try yourself:Find the value of  ..........… 50 terms.
..........… 50 terms.
Explanation
50th term =
Then,

Report a problem
Question for Practice Questions Level 1: Progressions, Sequences & Series - 1
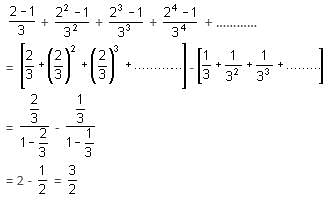
Try yourself:Find the sum of the infinite series: 1/3 + 3/9 + 7/27 + 15/81 + ............
Explanation
The given series can be written as:

Report a problem
Question for Practice Questions Level 1: Progressions, Sequences & Series - 1
Try yourself:If a, b, c and d are in GP, then (a - c)2 + (b - c)2 + (b - d)2 is equal to
Explanation
If a, b, c and d are in GP, then
b2 = ac, c2 = bd and ad = bc.
Given equation is:
a2 + c2 - 2ac + b2 + c2 - 2bc + b2 + d2 - 2bd
= [a2 + 2b2 + 2c2 + d2 - 2ac - 2bc - 2bd]
= [a2 + d2 + 2ac + 2bd - 2ac - 2bc - 2bd]
= [a2 + d2 - 2ad] = (a - d)2
Report a problem
Question for Practice Questions Level 1: Progressions, Sequences & Series - 1
Try yourself:The ninth term of an AP is 5 more than the sixth term. If the eleventh term of that AP is 35, then what is its first term?
Explanation
t9 = t6 + 5
⇒ a + 8d = a + 5d + 5
⇒ d = 5/3
t11 = a + 10d = 35

Report a problem
Question for Practice Questions Level 1: Progressions, Sequences & Series - 1
Try yourself:If x, y, z are in AP, then 
Explanation
x, y, z are in AP.
∴ 2y = (z + x)
Add (z + x) both sides.
2y + (z + x) = 2(z + x)
⇒ 2(z + x) = (y + z) + (x + y)
⇒ (y + z), (z + x), (x + y) are in AP.

Report a problem
Question for Practice Questions Level 1: Progressions, Sequences & Series - 1
Try yourself:The sum of 5 numbers in AP is 75 and the product of the greatest and the least of them is 161. What is the greatest number?
Explanation
Let the numbers be a - 2d, a - d, a, a + d, a + 2d.
Then, 5a = 75
a = 15
(a - 2d).(a + 2d) = 161
This implies, d = +4
Greatest term = 15 + 2 x 4 = 23
The greatest term would be the 5th term, if d = +4, and the 1st term, if d = -4.
Report a problem
Question for Practice Questions Level 1: Progressions, Sequences & Series - 1
Try yourself:The sum of the 9th, 14th and 18th terms of an AP is equal to the sum of the 20th and 24th terms. What is the ratio of the 4th term to the 2nd term?
Explanation
T9 + T14 + T18 = T20 + T24
⇒ 3a + 38d = 2a + 42d
⇒ a = 4d

Report a problem
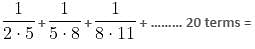
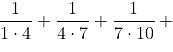 ..........… 50 terms.
..........… 50 terms.