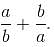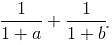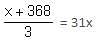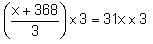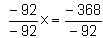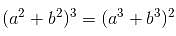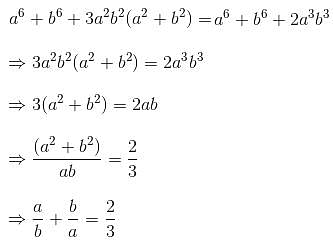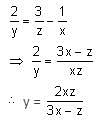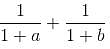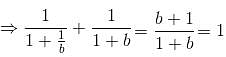This EduRev document offers 10 Multiple Choice Questions (MCQs) from the topic Quadratic Equations & Linear Equations (Level - 1). These questions are of Level - 1 difficulty and will assist you in the preparation of CAT & other MBA exams. You can practice/attempt these CAT Multiple Choice Questions (MCQs) and check the explanations for a better understanding of the topic.
Question for Practice Questions Level 1: Quadratic Equations & Linear Equations - 1
Try yourself:Total integer pair(s) (x, y) satisfying the equation x + y = xy is/are
Explanation
The equation is x + y = xy. The only two integer pairs satisfying this are (0, 0) and (2, 2).
Hence, there are 2 pairs.
Report a problem
Question for Practice Questions Level 1: Quadratic Equations & Linear Equations - 1
Try yourself:If A = 2 and B + P + F = 24, what are the values of Q and S? Consider whole numbers only.
A + B = Z, Z + P = T, T + A = F, F + S = Q, Q - T = 7
Explanation
Since it is known that A + B = Z, it follows that A + B + P = T.
We also know that T + A = F.
So, in the equation B + P + F = 24, we can replace F with T + A.
The equation then becomes B + P + T + A = 24 or B + P + T = 22, since A = 2.
Then, we have
B + P + 2 = T ... (i)
Since B + P + T = 22
-B - P + 22 = T ... (ii)
So, from equations (i) and (ii),
24 = 2T
So, T = 12
Now, 12 + A = 14 = F and Q - 12 = 7
So, Q = 19
Therefore, S = 5
Report a problem
Question for Practice Questions Level 1: Quadratic Equations & Linear Equations - 1
Try yourself:Which of the following is the correct value of x for the equation 
Explanation
Report a problem
Question for Practice Questions Level 1: Quadratic Equations & Linear Equations - 1
Try yourself:Let x and y be real numbers, such that (x2 - y2)(x2 - 2xy + y2) = 3 and x - y = 1. What is the value of xy?
Explanation
From the given information,
3 = (x2 - y2)(x2 - 2xy + y2)
3 = (x - y)(x + y)(x - y)2 = x + y (Because, it is given that x - y = 1)
Hence, 2x = (x + y) + (x - y) = 3 + 1 = 4 and 2y = (x + y) - (x - y) = 3 - 1 = 2
x = 2 and y = 1, so xy = 2.
Report a problem
Question for Practice Questions Level 1: Quadratic Equations & Linear Equations - 1
Try yourself:If p, q and r are the roots of the cubic equation x3 - 3x2 + 5x + k = 2 and pqr = 1, then find the value of k.
Explanation
If p, q and r are the roots of the cubic equation x3 - 3x2 + 5x + k - 2 = 0, then the product of the roots are as follows.
pqr = 2 - k (Using the formula of product of roots of a cubic equation)
k = 2 - 1
k = 1
Report a problem
Question for Practice Questions Level 1: Quadratic Equations & Linear Equations - 1
Try yourself:Find the value of x3 + y3 + z3 - 3xyz when x + y + z = 9 and xy + yz + zx = 11.
Explanation
(x3 + y3 + z3 - 3xyz) = (x + y + z)(x2 + y2 + z2 - xy - yz - zx)
= (x + y + z)[(x + y + z)2 - 3(xy + yz + zx)]
= 9(92 - 3 x 11) = 9(81 - 33) = 432
Report a problem
Question for Practice Questions Level 1: Quadratic Equations & Linear Equations - 1
Try yourself:If (a2 + b2)3 = (a3 + b3)2, then find the value of 
Explanation
Report a problem
Question for Practice Questions Level 1: Quadratic Equations & Linear Equations - 1
Try yourself:1/2 (a + b + c){(a - b)2 + (b - c)2 + (c - a)2} is equal to
Explanation
1/2 (a + b + c){(a - b)2 + (b - c)2 + (c - a)2}
1/2 (a + b + c){a2 + b2 – 2ab + b2 + c2 – 2bc + c2 + a2 – 2ca}
= (a + b + c)(a2 + b2 + c2 - ab - bc - ca)
= a3 + b3 + c3 - 3abc
Report a problem
Question for Practice Questions Level 1: Quadratic Equations & Linear Equations - 1
Try yourself:What is the value of y if 1/x + 2/y = 3/z ?
Explanation
Solving, we get:

Report a problem
Question for Practice Questions Level 1: Quadratic Equations & Linear Equations - 1
Try yourself:If x = ay and y = bx, where the values of x and y cannot be zero, find the value of 
Explanation
x = ay ... (i)
y = bx ... (ii)
Put the value of x in (ii).
y = b(ay)
⇒ a = 1/b ...(iii)
According to the question,

Put the value of 'a' from (iii).

Report a problem