This EduRev document offers 10 Multiple Choice Questions (MCQs) from the topic Speed, Time & Distance (Level - 1). These questions are of Level - 1 difficulty and will assist you in the preparation of CAT & other MBA exams. You can practice/attempt these CAT Multiple Choice Questions (MCQs) and check the explanations for a better understanding of the topic.
Question for Practice Questions Level 1: Speed, Time & Distance - 1
Try yourself:A train takes 8 seconds to pass a pole when it runs at a speed of 36 km/hr. Find the length of the train in metres.
Explanation
From question,
Length of the train (L) will be S × T.
L = (36 km/h) × (8 sec) = 36 × 1000/3600 × 8 = 80 m
Report a problem
Question for Practice Questions Level 1: Speed, Time & Distance - 1
Try yourself:Two trains running at speeds of 36 kmph and 54 kmph, respectively cross each other in 10 sec, if they run in opposite directions. When they run in the same direction, a person sitting in the faster train observes that he crossed the other train in 20 seconds. Find the lengths of the two trains.
Explanation
Let length of slower train-1 be L1 and length of faster train-2 be L2.
Relative speed when trains run in opposite directions = (54 + 36) × 5/18 = 25 m/s
So, 10 = (L1 + L2)/25
L1 + L2 = 250 ........(1)
Relative speed when trains run in the same direction = (54 - 36) × 5/18 = 5 m/s
Now,
20 = L1/5
L1 = 100 m ..........(2)
Put (2) in (1),
L2 = 150 m
Report a problem
Question for Practice Questions Level 1: Speed, Time & Distance - 1
Try yourself:The speeds of A and B are in the ratio 2 : 3. Starting from the same position, A takes 10 minutes more than the time taken by B to reach a certain destination. If A had walked at double the speed, then he would have covered the same distance in
Explanation
Given, both of them travel the same distance.
∴ Speed will be inversely proportional to time.
So, A and B will take 3x minutes and 2x minutes, respectively, to cover the same distance.
Given, 3x – 2x = 10
x = 10
So, A will take 30 minutes to cover the distance.
If A doubles his speed, then the time taken will be halved i.e. 15 minutes.
Report a problem
Question for Practice Questions Level 1: Speed, Time & Distance - 1
Try yourself:Without stoppages, a train travels with an average speed of 40 km/hr, while with stoppages, it covers the same distance with an average speed of 30 km/hr. What is the time (in minutes per hour) for which the train stops?
Explanation
Let the distance be the LCM of 40 and 30, i.e. 120 km.
So, without stoppages, time taken by train = 120/40 = 3 hr
With stoppages, time taken by train = 120/30 = 4 hr
Thus, in a total time of 4 hours, duration for which the train stops = 4 - 3 = 1 hr
Thus, in a total time of 1 hour, it would stop for 1/4 hour, i.e. 15 minutes.
Report a problem
Question for Practice Questions Level 1: Speed, Time & Distance - 1
Try yourself:An express train travelling at a speed of 72 km/hr crosses a goods train travelling at a speed of 45 km/hr in the opposite direction in half a minute. If the express train were to overtake the goods train while moving in the same direction, then how long would it take to do so? (Assume that the trains continue to travel at the same respective speeds as mentioned earlier.)
Explanation
Report a problem
Question for Practice Questions Level 1: Speed, Time & Distance - 1
Try yourself:The Sinhagad Express left Pune at noon sharp. Two hours later, the Deccan Queen started from Pune in the same direction. The Deccan Queen overtook the Sinhagad Express at 8 p.m. Find the average speed of the two trains over this journey if the sum of their average speeds is 70 km/h.
Explanation
The ratio of time for the travel is 4:3 (Sinhagad to Deccan Queen). Hence, the ratio of speeds would be 3:4.
Since, the sum of their average speeds is 70 kmph, their respective speeds would be 30 and 40 kmph respectively.
Use alligation to get the answer as 34.28 kmph.
Report a problem
Question for Practice Questions Level 1: Speed, Time & Distance - 1
Try yourself:Ram and Bharat travel the same distance at the rate of 6 km per hour and 10 km per hour respectively. If Ram takes 30 minutes longer than Bharat, the distance travelled by each is
Explanation
Since, the ratio of speeds is 3:5, the ratio of times would be 5:3.
The difference in the times would be 2 (if looked at in the 5:3 ratio context.)
Further, since Ram takes 30 minutes longer, 2 corresponds to 30.
Hence, using unitary method, 5 will correspond to 75 and 3 will correspond to 45 minutes.
Hence at 10 kmph, Bharat would travel 7.5 km.
Report a problem
Question for Practice Questions Level 1: Speed, Time & Distance - 1
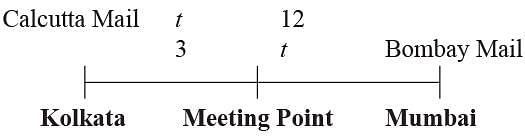
Try yourself:Two trains, Calcutta Mail and Bombay Mail, start at the same time from stations Kolkata and Mumbai respectively towards each other. After passing each other, they take 12 hours and 3 hours to reach Mumbai and Kolkata respectively. If the Calcutta Mail is moving at the speed of 48 km/h, the speed of the Bombay Mail is
Explanation
If you assume that the initial stretch of track is covered by the two trains in time t each, the following figure will give you a clearer picture.

From the above figure, we can deduce that, t/3 = 12/t.
Hence, t2 = 36, gives us t = 6.
Hence, the distance between Kolkata to the starting point is covered by the Calcutta Mail in 6 hours, while the same distance is covered by the Bombay Mail in 3 hours.
Hence, the ratio of their speeds would be 1:2. Hence, the Bombay Mail would travel at 96 kmph.
Report a problem
Question for Practice Questions Level 1: Speed, Time & Distance - 1
Try yourself:Lonavala and Khandala are two stations 600 km apart. A train starts from Lonavala and moves towards Khandala at the rate of 25 km/h. After two hours, another train starts from Khandala at the rate of 35 km/h. How far from Lonavala will they will cross each other?
Explanation
When the train from Khandala starts off, the train from Lonavala will already have covered 50 kms.
Hence, 550 km at a relative speed of 60 kmph will take 550/60 hrs.
From this, you can get the answer as:
50 + (550/60) * 25 = 279.166 km.
Report a problem
Question for Practice Questions Level 1: Speed, Time & Distance - 1
Try yourself:Alok walks to a viewpoint and returns to the starting point by his car and thus takes a total time of 6 hours 45 minutes. He would have gained 2 hours by driving both ways. How long would it have taken for him to walk both ways?
Explanation
Since he gains 2 hours by driving both ways (instead of walking one way) the time taken for driving would be 2 hours less than the time taken for walking.
Hence, he stands to lose another two hours by walking both ways.
Hence his total time should be 8 hrs 45 minutes.
Report a problem


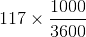 =
= 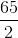 m/sec
m/sec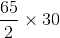 = 975 metres
= 975 metres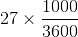 =
= 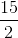 m/sec
m/sec 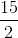 × Time taken (in seconds)
× Time taken (in seconds) 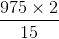 = 130 seconds
= 130 seconds