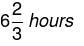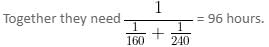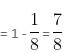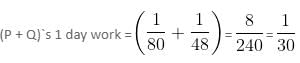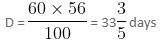This EduRev document offers 10 Multiple Choice Questions (MCQs) from the topic Time & Work (Level - 1). These questions are of Level - 1 difficulty and will assist you in the preparation of CAT & other MBA exams. You can practice/attempt these CAT Multiple Choice Questions (MCQs) and check the explanations for a better understanding of the topic.
Question for Practice Questions Level 1: Time & Work - 1
Try yourself:A and B can do a piece of work in 10 days and A alone can do it in 15 days. In how many days can B alone do it?
Explanation
Total time taken by A and B together to finish the work = 10 days
And time taken by A alone to finish the work = 15 days
∴ A and B together can do 1/10 of the work in one day and A can do 1/15 of the work in a day.
Work done by B in one day
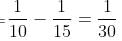
So, B takes 30 days to do the work alone.
Report a problem
Question for Practice Questions Level 1: Time & Work - 1
Try yourself:20 men can complete a work in 50 days, working for 5 hours a day. After 15 days from the start of work, 10 men quit. How many hours per day do the remaining men have to work so as to complete the work on time?
Explanation
Total Work = Number of workers × number of days × number of hours = 20 × 50 × 5 = 5000 units
Let remaining 10 men have to work n hours a day. So, remaining 10 workers work for 35 days.
Total Work = Work done by 20 workers in '15' days working 5 hours a day + Work done by 10 workers in 35 days working n hours a day.
5000 units = 20 × 15 × 5 + 10 × 35 × n
n = 10 hours
Report a problem
Question for Practice Questions Level 1: Time & Work - 1
Try yourself:A contractor employs 200 men to build a dam. They finish 5/6 part of the work in 10 weeks. Due to rain, the work remains suspended for 4 weeks and also half of the work already done is washed away. When the work is resumed, only 140 men turn up. The total time in which the contractor is able to complete the work is (Assuming there are no further disruptions)
Explanation
Report a problem
Question for Practice Questions Level 1: Time & Work - 1
Try yourself:A contractor was asked to build a garage. He employed a number of men of equal efficiency. They could finish the job in 6 hours if they worked simultaneously, but he told them to begin one after the other, such that the intervals between their starting times should be equal. After the last worker had begun working, a time interval of the same length elapsed and the job was finished. Each one of the workers worked till the completion of the job. If the first man to begin worked 5 times as long as the last one to begin, in how many hours was the garage built?
Explanation
Since the workers began working one after the other, the interval between their starting times is the same. The first to begin worked five times as long as the last to begin. The number of workers is equal to 5.
If the last worker to begin worked for x hours, then the total working hours = x + 2x + 3x + 4x + 5x = 15x
The men could have finished the work in 6 hours, had they begun at the same time, i.e. 15x = 5 × 6 or x = 2
The job lasted for 5x = 10 hours.
Report a problem
Question for Practice Questions Level 1: Time & Work - 1
Try yourself:An inlet pipe A lets water in a tank at 2 litres per minute and another pipe B lets water in at 3 litres per minute. There is an outlet pipe at the bottom, which can empty the tank in 10 hours. If all the three pipes were kept on, then the tank would be filled in 8 hours. What is the capacity of the tank?
Explanation
In 8 hours, the outlet pipe can empty 8/10 of the tank.
So, in 8 hours, both the inlet pipes together will fill 18/10 of the tank.
18/10 tank = (2 + 3 litres) × 60 × 8 litres = 2400 litres
Capacity of the tank
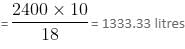
Report a problem
Question for Practice Questions Level 1: Time & Work - 1
Try yourself:Tap 'x' can fill the tank in 8 hours. Tap 'y' can empty it in 12 hours. Both the taps were opened for 4 hours and then, tap 'y' was closed. How much more time will it take to fill the tank completely?
Explanation
In 1 hour, pipe 'x' can fill 1/8 part of the tank.
In 1 hour, pipe 'y' can empty 1/12 part of the tank.
In 1 hour, both pipes can fill = 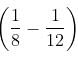 part = 1/24 part of the tank.
part = 1/24 part of the tank.
In 4 hours, both x and y can fill 1/6 part of the tank.
So to fill 5/6th of the tank, tap x will take 5/6 × 8 = 20/3 = 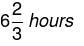
Report a problem
Question for Practice Questions Level 1: Time & Work - 1
Try yourself:Water flows from a pipe of sectional area 500 cm2 at the rate of 8 m/min. How long would it take to fill a tank whose dimensions are 6 m × 4 m × 4 m?
Explanation
Let the required time be p hours.
Then, Volume of water flowing through pipe in p hours = Volume of the cistern
⇒ 500 × 10-4 × 8 × 60 × p = 6 × 4 × 4
⇒ p = 4
Report a problem
Question for Practice Questions Level 1: Time & Work - 1
Try yourself:A and B, working 8 hours a day, can do a piece of work in 20 days and 30 days, respectively. On weekends, they work for only 1 hour and on weekdays, they work for 4 hours. If they start working together on Sunday, then on which day will they finish the task? (Assume that weekend includes Saturday and Sunday)
Explanation
A needs 160 hours and B needs 240 hours to complete the work separately.
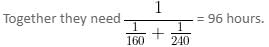
In 1 week, they will work for (2 × 1 + 5 × 4) = 22 hours.
In 4 weeks, they will work for 88 hours.
On Tuesday of the fifth week, they will finish their work.
Report a problem
Question for Practice Questions Level 1: Time & Work - 1
Try yourself:P can do a piece of work in 80 days. He works at it for 10 days and then Q alone finishes the remaining work in 42 days. The two together would have completed the work in
Explanation
Report a problem
Question for Practice Questions Level 1: Time & Work - 1
Try yourself:A group of 60 men can complete a piece of work in a certain number of days. If 10 more men join them, then the work can be completed in 8 days less. How many days will be required to complete the same work by 100 men?
Explanation
Let the amount of work done by 1 man in 1 day be w.
Let the total number of days taken initially to complete the work be d.
Let the amount of total work be W.
So, 60dw = W ...(i)
Now, when 70 men do the work, it takes 8 days less.
So, 70w(d - 8) = W ...(ii)
Equating (i) and (ii), we get:
60d = 70(d - 8)
d = 56
So, W = w × 60 × 56
Now, let 100 men take D days to complete the work.
So, 100 × D × w = W = w × 60 × 56
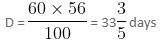
Report a problem






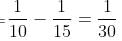
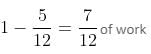
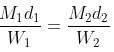
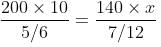
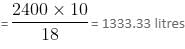
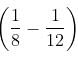 part = 1/24 part of the tank.
part = 1/24 part of the tank.