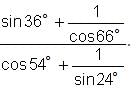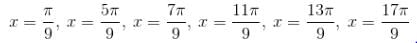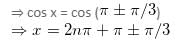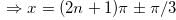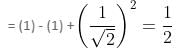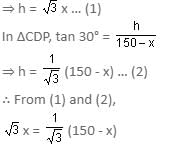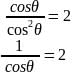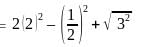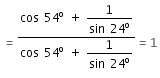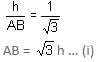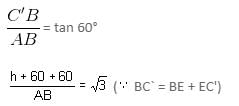This EduRev document offers 10 Multiple Choice Questions (MCQs) from the topic Trigonometry (Level - 1). These questions are of Level - 1 difficulty and will assist you in the preparation of CAT & other MBA exams. You can practice/attempt these CAT Multiple Choice Questions (MCQs) and check the explanations for a better understanding of the topic.
Question for Practice Questions Level 1: Trigonometry - 1
Try yourself:If cot (x + 27°) = tan y, then which of the following equations is true?
Explanation
cot (90 - θ) = tan θ
So, tan y = cot (90° - y)
Hence, cot (x + 27°) = cot (90° - y)
x + 27° = 90° - y
x + y = 90° - 27° = 63°
Report a problem
Question for Practice Questions Level 1: Trigonometry - 1
Try yourself:Solve for x: 2 cos (3x) - 1 = 0; where, x ∈ (0, 2π)
Explanation
2 cos 3x - 1 = 0
⇒ cos 3x = 1/2 = cos 60°
The general solution of above equation is

The solution in the interval (0, 2π) are
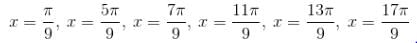
Hence, correct answer that match the given options are 20°, 100°
Report a problem
Question for Practice Questions Level 1: Trigonometry - 1
Try yourself:The value of cos 24° + cos 55° + cos 125° + cos 204° + cos 300° is
Explanation
The value of cos 24° + cos 55° + cos 125° + cos 204° + cos 300° ?
We know that, cos(180° ± θ) = - cosθ
⇒ cos 24° + cos 55° + cos(180° - 55°) + cos(180° + 24°) + cos(360° - 60°)
= cos 24° + cos 55° - cos 55° - cos 24° + cos 60°
= cos 60° = 1/2
Report a problem
Question for Practice Questions Level 1: Trigonometry - 1
Try yourself:Solve the equation 2 sin2 x + 3 cos x = 0.
Explanation
2 sin2 x + 3 cos x = 0
⇒ 2(1 - cos2 x) + 3 cos x = 0
⇒ 2 - 2 cos2 x + 3 cos x = 0
⇒ 2 cos2 x - 3 cos x - 2 = 0
⇒ 2 cos2 x - 4 cos x + cos x - 2 = 0
⇒ 2 cos x(cos x - 2) + 1(cos x - 2) = 0
⇒ (cos x - 2)(2 cos x + 1) = 0
Either cos x - 2 = 0 or 2 cos x + 1 = 0
But cos x - 2 = 0
i.e. cos x = 2, which is not possible.
Now, from 2 cos x + 1 = 0, we get:
cos x = -1/2
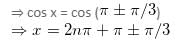
Therefore, general solution of the equation is:
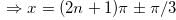
Report a problem
Question for Practice Questions Level 1: Trigonometry - 1
Try yourself:Find the value of cos2 15° - cos2 30° + cos2 45° - cos2 60° + cos2 75°.
Explanation
cos2 15° - cos2 30° + cos2 45° - cos2 60° + cos2 75° = (cos2 15° + cos2 75°) - (cos2 30° + cos2 60°) + cos2 45°
= [cos2 15° + cos2 (90° - 15°)] - [cos2 30° + cos2 (90° - 30°)] + cos2 45°
= [cos2 15° + sin2 15°] - [cos2 30° + sin2 30°] + cos2 45° [∵ cos (90° - θ) = sin θ]
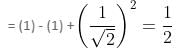
Report a problem
Question for Practice Questions Level 1: Trigonometry - 1
Try yourself:Two pillars of equal height stand on either side of a road, which is 150 m wide. At a point on the road between the pillars, the angles of elevation of their tops are 60° and 30°. Find the height of the pillars.
Explanation
Let AB and CD be the two pillars of equal height 'h' m.
If P is the point between them, then
∠APB = 60° and ∠CPD = 30°
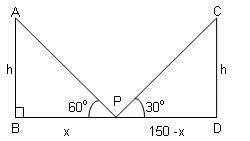
Let BP = x m
⇒ PD = (150 - x) m
In ΔABP, tan 60° =
⇒ h = √3x … (1)
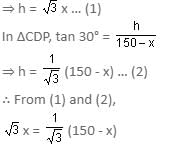
⇒ 3x = 150 - x or 4x = 150
∴ x = 37.5 and h = √3x = (1.732)37.5 = 64.95 m
Report a problem
Question for Practice Questions Level 1: Trigonometry - 1
Try yourself:If cosθ = 2cos2θ , then 2sec2θ – cos2θ + tan2θ =
Explanation
Report a problem
Question for Practice Questions Level 1: Trigonometry - 1
Try yourself:Find the value of
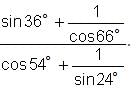
Explanation

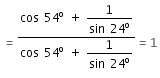
(∵ sin (90° - θ) = cos θ and cos (90° - θ) = sin θ)
Report a problem
Question for Practice Questions Level 1: Trigonometry - 1
Try yourself:The angle of elevation of a cloud from a point 60 m above a lake is 30° and the angle of depression of its image in lake is 60°. The height of the cloud is
Explanation
Let A be the point of observation and C be the position of the cloud. Let DE be the surface of the lake and C' be the reflection of C in the lake.
∠CAB = 30°
And ∠C'AB = 60°
Let BC = h m
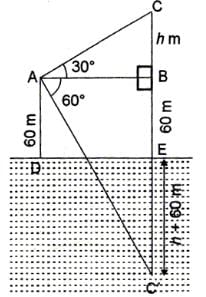
In right-angled ΔABC, BC/AB = tan 30°
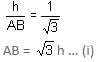
In right-angled ΔABC',
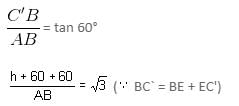
h = 60 m
Height of cloud = 120 m
Report a problem
Question for Practice Questions Level 1: Trigonometry - 1
Try yourself:Solve for the number of solution of the equation: sin(x) + cos(x) = 1 on the interval 0° ≤ x < 360°.
Explanation
sin(x) + cos(x) = 1
Squaring both side,
(sin(x) + cos(x))2 = 12
[sin2(x) + cos2(x)] + 2sin(x)cos(x) = 1 (Using identity: (a + b)2 = a2 + b2 + 2ab)
1 + 2sin(x)cos(x) = 1
2sin(x)cos(x) = 0
sin(x)cos(x) = 0
From the last line above, either sine is zero or cosine is zero, so solutions are:
x = 0°, 90°, 180°, 270°
Checking the value of 'x' in the above equation,
x = 0°, 90° satisfies.
x = 180° and 270° does not satisfies.
Hence, total number of solution = 2
Report a problem