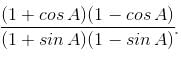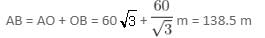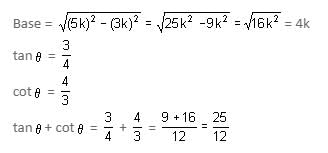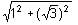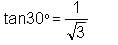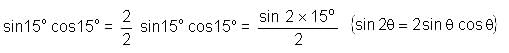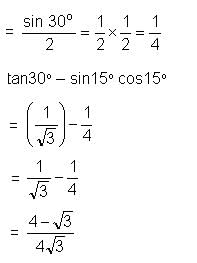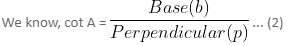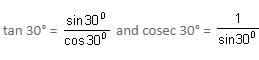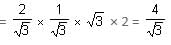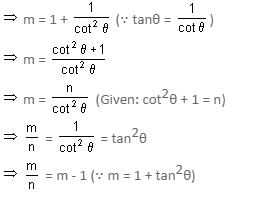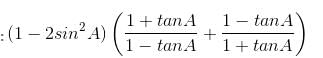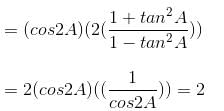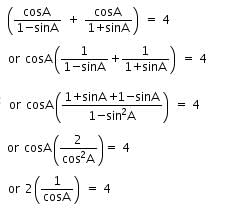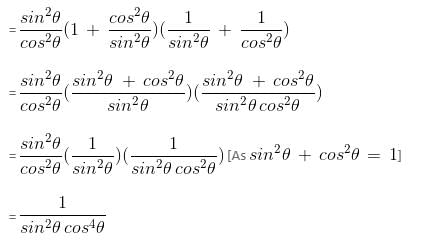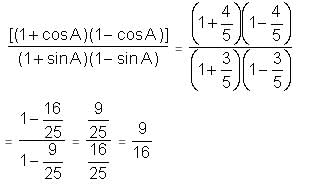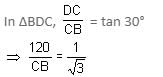This EduRev document offers 15 Multiple Choice Questions (MCQs) from the topic Trigonometry (Level - 1). These questions are of Level - 1 difficulty and will assist you in the preparation of CAT & other MBA exams. You can practice/attempt these CAT Multiple Choice Questions (MCQs) and check the explanations for a better understanding of the topic.
Question for Practice Questions Level 1: Trigonometry - 2
Try yourself:From a 60 m high building, the angles of depression of two cars on the opposite ends of the building are observed to be 60° and 30°. Find the distance between the cars, if the line joining them passes through the foot of the building.
Explanation
Suppose OP is the building, and A and B are the two cars. Then, OP = 60, PAO = 60° and PBO = 30°
From the right triangle OBP, tan 30° = 60/OB
OB = 60 √m ...(i)
Also, from the right triangle AOP, tan 60° = 60/OA
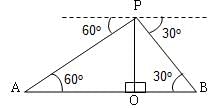
OA = 60/√3 ....(ii)
Thus, from (i) and (ii),
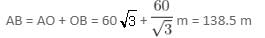
Report a problem
Question for Practice Questions Level 1: Trigonometry - 2
Try yourself:If 10 sinθ = 6, then tanθ + cotθ =
Explanation
If 10 sinθ = 6,
sinθ = 6/10 = 3/5
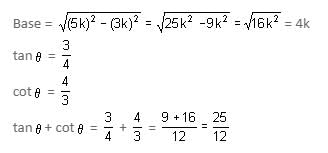
Report a problem
Question for Practice Questions Level 1: Trigonometry - 2
Try yourself:A right triangle PQR is right-angled at Q. If tan R = 1/√3, then which of the following is the value of sin R?
Explanation
In a right-angled triangle PQR with ∠Q = 90°:
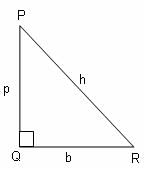
sin R = p/h , cos R = b/h, tan R = p/b, cosec R = h/p , sec R = h/b and cot R = b/p.
Here, p stands for perpendicular, b stands for base and h stands for hypotenuse.
Now, in ΔPQR, tan R = 1/√3 ……… (1)
Also, tan R = p/b……… (2)
On comparing (1) and (2), we get
p = 1 and b = √3
Using Pythagoras theorem:
h2 = p2 + b2
h = 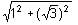
h = 2
Thus, p = 1 and h = 2
So, sin R = p/h = 1/2.
Report a problem
Question for Practice Questions Level 1: Trigonometry - 2
Try yourself:If sin 30° = 1/2 , the value of expression tan 30° - sin 15° cos 15° is
Explanation
Report a problem
Question for Practice Questions Level 1: Trigonometry - 2
Try yourself:In a right triangle ABC, right-angled at B, cot2 A = 9/16. What is the value of cos A?
Explanation
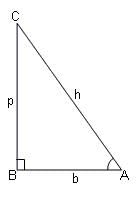
In right ΔABC,
∠B = 90°, cot2 A = 9/16
Taking square root on both sides, we get
cot A = 3/4… (1)
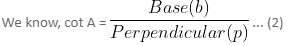
From (1) and (2), we get
b/p = 3/4
⇒ b = 3k and p = 4k
Now, using Pythagoras theorem,
AC2 = AB2 + BC2
h2 = p2 + b2
= (4k)2 + (3k)2
= 16k2 + 9k2
= 25k2
h = 5k
cos A = b/h = 3/5
Report a problem
Question for Practice Questions Level 1: Trigonometry - 2
Try yourself:Find the value of sec 30° cot 30° tan 30° cosec 30°.
Explanation

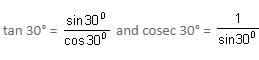
Therefore, sec 30° = 2/√3 = cosec 30° = 2, tan 30° = 1/√3 and cot 30° = √3
Hence, sec 30° tan 30° cot 30° cosec 30°
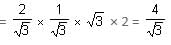
Report a problem
Question for Practice Questions Level 1: Trigonometry - 2
Try yourself:If m = 1 + tan2θ and n = 1 + cot2θ, then m/n equals
Explanation
1 + tan2θ = sec2θ,
1 + cot2θ = cosec2θ
and cotθ = 1/tanθ
Given:
m = 1 + tan2θ
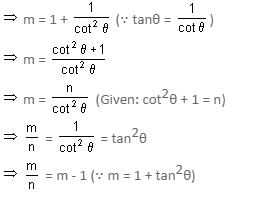
Report a problem
Question for Practice Questions Level 1: Trigonometry - 2
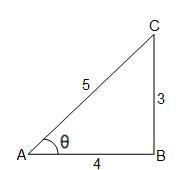
Try yourself:If sinθ = 3/5, then find the value of (cosθ + tanθ + cotθ).
Explanation
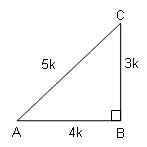
When sinθ = 3/5, we can draw a triangle as shown in the figure.
sinθ = CB/AC = 3/5 (given)
cosθ = AB/AC = 4/5
tanθ = BC/AB = 3/4
cotθ = AB/BC = 4/3
cosθ + tanθ + cotθ = (4/5) + (3/4) + (4/3)
= (48 + 45 + 80)/60 = 173/60
Report a problem
Question for Practice Questions Level 1: Trigonometry - 2
Try yourself:
Explanation
Report a problem
Question for Practice Questions Level 1: Trigonometry - 2
Try yourself: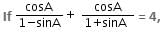 then what is the value of A?
then what is the value of A?
Explanation
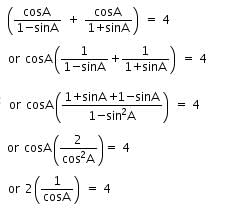
or sec A = 2
or sec A = sec 60°
or A = 60°
Therefore, option (1) is correct.
Report a problem
Question for Practice Questions Level 1: Trigonometry - 2
Try yourself:From the top of a 10 m high building, the angle of elevation of the top of a tower is 45° and the angle of depression of its foot is 60°. How will you represent this situation diagrammatically?
Explanation
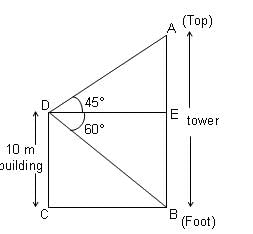
The observer is at point 'D'.
Report a problem
Question for Practice Questions Level 1: Trigonometry - 2
Try yourself:The reduced form of cos6 x + sin6 x + 3 cos2 x.sin2 x is _______________.
Explanation
We know that,
cos2 x + sin2 x = 1
Taking the third power,
(cos2 x + sin2 x)3 = cos6 x + sin6 x + 3 cos2 x sin4x + 3 sin2 x cos4 x = 1
i.e. cos6 x + sin6 x + 3 cos2 x sin2 x (sin2 x + cos2x) = 1
cos6 x + sin6 x + 3 cos2 x sin2 x = 1
Report a problem
Question for Practice Questions Level 1: Trigonometry - 2
Try yourself:tan2θ (1 + cot2θ) (cosec2θ + sec2θ)
Explanation
tan2θ (1 + cot2θ) (cosec2θ + sec2θ)
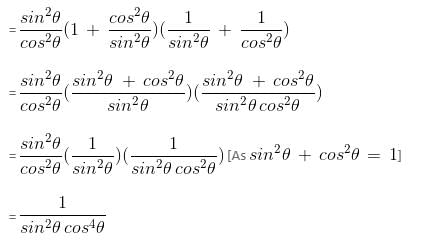
Report a problem
Question for Practice Questions Level 1: Trigonometry - 2
Try yourself:If in a right triangle, tan A = 3/4 , then find the value of
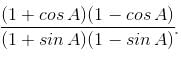
Explanation
tan A = 3/4
⇒ sin A = 3/5 and cos A = 4/5
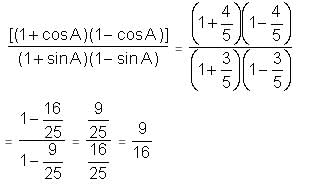
Report a problem
Question for Practice Questions Level 1: Trigonometry - 2
Try yourself:From two points A and B on the opposite sides of a tower, the angles of elevation to the top of the tower are 45° and 30°, respectively. If the height of the tower is 120 m, then find the distance between A and B, corrected to two decimal places.
Explanation
Let the length of the tower be CD.
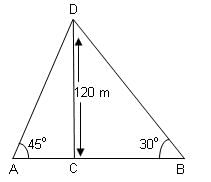
CD = 120 m
∠DAC = 45° and DBC = 30°
In ΔADC,
DC/AC = tan 45°
120/AC = 1
AC = 120 m
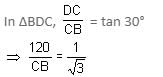
CB = 120 × 1.732
CB = 207.84 m
Thus, distance between points A and B
= AC + CB = 120 + 207.84 = 327.84 m
Report a problem

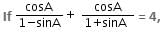 then what is the value of A?
then what is the value of A?