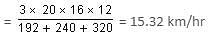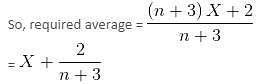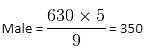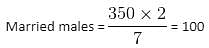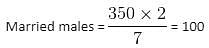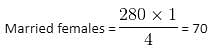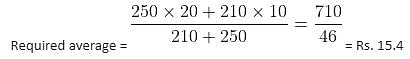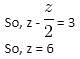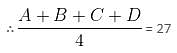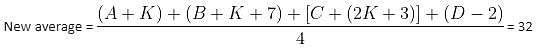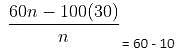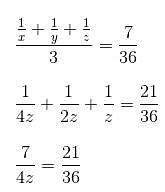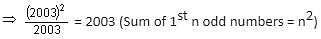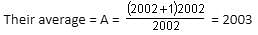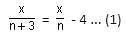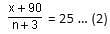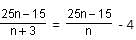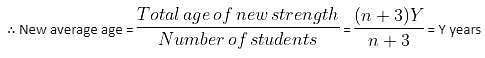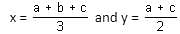This EduRev document offers 20 Multiple Choice Questions (MCQs) from the topic Averages (Level - 2). These questions are of Level - 2 difficulty and will assist you in the preparation of CAT & other MBA exams. You can practice/attempt these CAT Multiple Choice Questions (MCQs) and check the explanations for a better understanding of the topic.
Question for Practice Questions Level 2: Averages - 2
Try yourself:The average of x and y is 4 and both x and y are positive integers. How many pairs of (x, y) satisfy this condition?
Explanation
Here, total sum of x + y should be equal to 8 and for that, the pairs of x and y are (1, 7), (2, 6), (3, 5), (4, 4), (7, 1), (6, 2) and (5, 3).
Hence, there are total 7 pairs.
Report a problem
Question for Practice Questions Level 2: Averages - 2
Try yourself:The average speed of a cyclist who covers first, second and third km at speeds of 20 km/hr, 16 km/hr and 12 km/hr, respectively, is
Explanation


Direct formula:
Average speed = 3abc/(ab+ bc+ca)
(where a, b, c are the different speeds for different km)
Report a problem
Question for Practice Questions Level 2: Averages - 2
Try yourself:The average age of a class of n boys is X years. Three new boys join the class whose ages are X - 1, X + 1 and X + 2 years, respectively. What is the new average age of the class?
Explanation
Average age of class of n boys = X
Total age of n boys = nX
After 3 students join the class, total age of (n + 3) boys
= nX + X - 1 + X + 1 + X + 2
= nX + 3X + 2
= (n + 3)X + 2

Report a problem
Question for Practice Questions Level 2: Averages - 2
Try yourself:The average age of a family of 5 members is 22 years. If the age of the youngest member is 10 years, then what was the average age of the family at the birth of the youngest member?
Explanation
Sum of ages of 5 members = 5 × 22 = 110 years
The youngest member is of 10 years.
Now, excluding the youngest member, sum of ages of the rest 4 members = 110 - 10 = 100 years
10 years ago, sum of ages = 100 - (4 × 10) = 60
Thus, average of 4 members = 60/4 = 15 years
Report a problem
Question for Practice Questions Level 2: Averages - 2
Try yourself:The average weight of a class of 35 students is 47.5 kg. If the weight of the teacher is included, the average rises by 500 g. The weight of the teacher is
Explanation
Average weight of 35 students = 47.5 kg
Total weight of 35 students = 35 × 47.5 = 1662.5 kg
Average weight of 36 people = 47.5 + 0.5 = 48 kg
Total weight of 36 people = 36 × 48 = 1728
Therefore, weight of the teacher = 1728 - 1662.5 = 65.5 kg
Report a problem
Question for Practice Questions Level 2: Averages - 2
Try yourself:The average marks of students A, B and C are 48. Another student (D) joins the group and the new average becomes 44 marks. If again, another student (E), who has three marks more than D, joins the group, the average of students B, C, D and E becomes 43 marks. How many marks did A get in the exam?
Explanation
A + B + C = 48 × 3 = 144 ............(i)
A + B + C + D = 44 × 4 = 176 ............(ii)
(ii) - (i) gives, D = 176 - 144 = 32
Marks of E = 32 + 3 = 35
B + C + D + E = 43 × 4 = 172
B + C + D = 172 - 35 = 137 .........(iii)
(ii) - (iii) gives,
A = 176 - 137
A = 39
Report a problem
Question for Practice Questions Level 2: Averages - 2
Try yourself:In a party the ratio of male and female is 5 : 4, the ratio of married and bachelor males is 2 : 5 and the ratio of married and unmarried females is 1 : 3. Total persons in the party are 630. If a man contributes Rs. 20 and a female Rs. 10, then what is the average contribution (in Rs.) per head by unmarried persons?
Explanation
Total persons = 630
Male : Female = 5 : 4

Females = 630 - 350 = 280


Bachelor males = 350 - 100 = 250


Unmarried females = 280 - 70 = 210

Report a problem
Question for Practice Questions Level 2: Averages - 2
Try yourself:Average of three numbers is x. Instead of the first number if we take only half of that number, the average will be x - 1. If twice the first number is taken in place of the first number, what will be the average?
Explanation
If half of the first number is removed, the average decreases by 1, that means, the total decreases by 3.We assume that the number is z.

Therefore, if we take 2z instead of z, the total will increase by 6 and the average increases by 2.
So, it will be x + 2.
Report a problem
Question for Practice Questions Level 2: Averages - 2
Try yourself:Total expenses of a boarding house are partly fixed and partly varying linearly with the number of boarders. The average expense per boarder is Rs. 700 when there are 25 boarders, and Rs. 600 when there are 50 boarders. What will be the average expense per boarder when there are 100 boarders?
Explanation
Let x be the fixed cost and y be the variable cost.
17,500 = x + 25y ……..(i)
30,000 = x + 50y ……..(ii)
Solving the equations (i) and (ii), we get
x = 5,000, y = 500
Now, if the average expense of 100 boarders be `A`, then
100 × A = 5,000 + 500 × 100
∴ A = 550
Report a problem
Question for Practice Questions Level 2: Averages - 2
Try yourself:The average of four numbers is 27. If the first number is increased by K, the second by (K + 7), the third by (2K + 3) and the fourth is decreased by 2, then the new average of the four numbers will become 32. Find the value of K.
Explanation
It is given that average of the four numbers is 27.
Let A, B, C and D be the four numbers.

A + B + C + D = 108 … (1)
Also, A is increased by K; A + K.
B is increased by K + 7; B + K + 7.
C is increased by 2K + 3; C + 2K + 3.
D is decreased by 2; D – 2.

⇒ A + B + C + D + 4K = 128 – 8 = 120
⇒ 108 + 4K = 120 {From equation (1)}
⇒ 4K = 12
K = 3
Report a problem
Question for Practice Questions Level 2: Averages - 2
Try yourself:Amol was asked to calculate the arithmetic mean of ten positive integers, each of which had two digits. By mistake, he interchanged the two digits, say a and b, in one of these ten integers i.e. ab. As a result, his answer for the arithmetic mean was 1.8 more than what it should have been. Then, b - a is equal to
Explanation
The original number is ab.
Let the sum of the rest nine terms be x.
Average before the digits were interchanged = [(x/10) + (10a + b)/10]
Average after the digits were interchanged = [(x/10) + (10b + a)/10]
Given;
[(x/10) + (10b + a)/10] - [(x/10) + (10a + b)/10] = 1.8
(b - a) - (b - a)/10 = 1.8
9(b - a)/10 = 1.8
(b - a) = 2
Report a problem
Question for Practice Questions Level 2: Averages - 2
Try yourself:In an exam, the average score of the candidates was found to be 60. After deducting computational errors, the scores of 100 candidates had to be changed from 80 to 50 each, and the overall average score of students had to be reduced by 10. What was the total number of students in the class?
Explanation
Let there be n students in the class.
Total marks = 60n
After deducting computational errors,
we have:

⇒ 60n - 3000 = 50n
⇒ 10n = 3000
⇒ n = 300
So, there were 300 students in the class.
Report a problem
Question for Practice Questions Level 2: Averages - 2
Try yourself:Mr. Rajan takes three numbers. Out of these three numbers, the second is twice the third and the first is twice the second. The average of the reciprocal of the numbers is 7/36. Find the sum of all the three numbers.
Explanation
Let the three numbers be x, y and z.
Now, according to the question,
y = 2z and x = 2y = 4z
Also, average of the reciprocal = 7/36

After solving this, we get:
z = 3
Then,
x = 12
y = 6
Sum of all three numbers = 21
Report a problem
Question for Practice Questions Level 2: Averages - 2
Try yourself:A publisher incurs a fixed expense of Rs. 2,000 towards composing and other activities in printing books. A variable cost of Rs. 2.25 per book is incurred towards paper, binding charges etc. What is the average cost per book if 40,000 copies are printed?
Explanation
Fixed expense = Rs. 2,000
Variable cost per book = Rs. 2.25
Then, variable cost for 40,000 books = Rs. 2.25 40,000 = Rs. 90,000
Total cost of 40,000 books = Rs. 90,000 + Rs. 2,000 = Rs. 92,000
Average cost per book = 92,000/40,000 = Rs. 2.30
OR
The average cost per book = 2.25 + 2000/40000= 2.30
Report a problem
Question for Practice Questions Level 2: Averages - 2
Try yourself:There are some consecutive numbers and 'x' is the average of all the numbers, except the first number. If 'y' is the average of all the numbers, except the last number, then what is the value of x - y?
Explanation
In both the cases, the number of items is the same.
Since the average is the middle number, the middle number in the first case is just one more than that in the second case.
So, x - y = 1
Report a problem
Question for Practice Questions Level 2: Averages - 2
Try yourself:P = {1, 2, 3, 4… 2n + 1} is a set, where n is a positive integer and n > 2000. If A is the average of all the even numbers of the set P and B is the average of all the odd numbers of the set P, then what is the difference between A and B?
Explanation
2n + 1 is always odd, what ever may be the value of n.
So, P is a set of consecutive numbers starting and ending with odd numbers.
Out of total (2n + 1) terms, we have (n + 1) number of odd terms and n number of even terms.
Let us take n = 2002
Total odd numbers = 2003 and their average = B = Sum of 1st 2003 odd numbers, divided by 2003

Total even numbers = 2002

So, difference between them = 0
Or,
A is the average of 2, 4, 6,..........., 2n = [n(n + 1)]/n = n + 1
B is the average of 1, 3, 5,........., 2n + 1 = (n + 1)2/(n + 1) = n + 1
A - B = 0
Report a problem
Question for Practice Questions Level 2: Averages - 2
Try yourself:An enterprise got a bonus and decided to share it in equal parts between the workers. Three more workers joined the enterprise. Hence, each of them got 4 rupees less. The administration had found the possibility to increase the total sum of the bonus by 90 rupees and as a result, each worker including the three new workers got 25 rupees. How many total workers are there now?
Explanation
Let total bonus = x and number of workers = n
Each worker gets x/n
Condition (1):

Condition (2):

Solving (2), we get
x = 25n - 15
From (1), we get

25n2 - 15n = 25n2 - 15n + 75n - 45 - 4n2 - 12n
4n2 - 63n + 45 = 0
n = 15 (as n cannot be in fractions)
Total workers now = n + 3 = 18
Report a problem
Question for Practice Questions Level 2: Averages - 2
Try yourself:The present average age of n boys in Class VIII is Y years. Three new boys join the class, whose ages are Y - 1, Y - 2 and Y + 3 years. What will be the new average age (in years) of the class, when all the students are promoted to Class X(tenth)?
Explanation
Given average age of class of n boys is Y years.
Total age of n boys = n × Y = nY years
Three new boys that join the class are of ages (Y - 1), (Y - 2) and (Y + 3) years.
New total age of the boys will be
[nY + (Y - 1) + (Y - 2) + (Y + 3)] years = nY + 3Y = (n + 3)Y

The students will be in Class X after 2 years.
So, average age of the class after 2 years = (Y + 2) years
Alternate method:
Sum of the ages of the three new boys = 3Y
⇒ The average age of the class does not change.
⇒ Average age will be Y years.
So, when they are promoted to Class X (i.e. gap of 2 years), the average age will be (Y + 2) years.
Report a problem
Question for Practice Questions Level 2: Averages - 2
Try yourself:A salesman gets a bonus of Rs. (3x + 7), if he sells articles worth Rs. x2. Apart from this, he receives a basic salary, which is 50 times his total bonus. In the month of January, the value of his sale was Rs. 100, in February, it was Rs. 400, and from March to December, it was Rs. 900 each month. Find his average salary per month for the year.
Explanation
His bonus in January = 3 × 10 + 7 = Rs. 37
His bonus in February = 3 × 20 + 7 = Rs. 67
His bonus per month from March to December = 3 × 30 + 7 = Rs. 97
Total bonus = 37 + 67 + 10 × 97 = Rs. 1074
Total basic salary = 50 × 1074 = Rs. 53,700

Report a problem
Question for Practice Questions Level 2: Averages - 2
Try yourself:x is the average of three different integers, y is the average of minimum and maximum integers among the three. If x is two more than y, what is the difference between x and the third integer, which is neither minimum nor maximum?
Explanation
Assume a, b and c are the numbers. a > b > c

a + b + c = 3x
a + c = 3x – b
2y = 3 x – b
2(x – 2) = 3x – b
2x – 4 = 3x – b
x – b = - 4
So, the difference between x and b is 4.
Report a problem