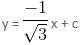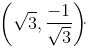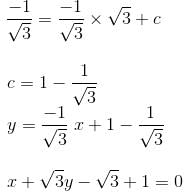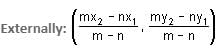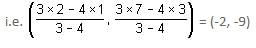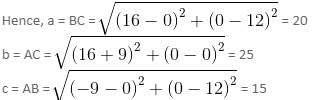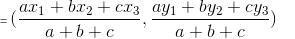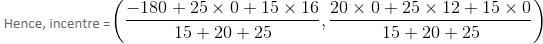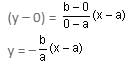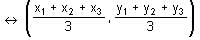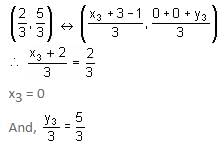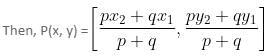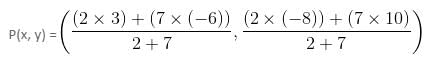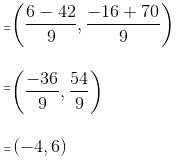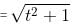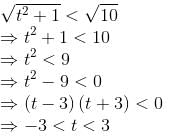This EduRev document offers 20 Multiple Choice Questions (MCQs) from the topic Coordinate Geometry (Level - 2). These questions are of Level - 2 difficulty and will assist you in the preparation of CAT & other MBA exams. You can practice/attempt these CAT Multiple Choice Questions (MCQs) and check the explanations for a better understanding of the topic.
Question for Practice Questions Level 2: Coordinate Geometry - 2
Try yourself:What kind of a quadrilateral is formed by the vertices (0, 0), (4, 3), (3, 5) and (-1, 2)?
Explanation
Let the points be A(0, 0), B(4, 3), C(3, 5) and D(-1, 2)
Let A and B be the easy points then,
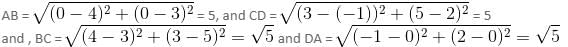
The sides are equal. So, the quadrilateral is at least a parallelogram.
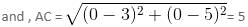
and (AC)2 ≠ (AB)2 + (BC)2
Therefore, the quadrilateral is not rectangle.
So, the given quadrilateral is a parallelogram.
Report a problem
Question for Practice Questions Level 2: Coordinate Geometry - 2
Try yourself:If a, b, c are in A.P. then the fixed point through which the straight line ax + 2by + c = 0 will always pass, is
Explanation
Since, a, b, c are in A.P.
So, 2b = a + c.
Now, only (1, -1) satisfies the equation.
Report a problem
Question for Practice Questions Level 2: Coordinate Geometry - 2
Try yourself:In the above figure, if O(0, 0) is the centre of the circle, then which of the following points lies outside the circle?
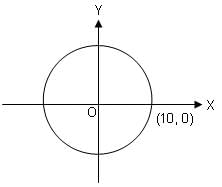
Explanation
A point will be outside the given circle if its distance from the centre, i.e. origin O, is more than 10.
Now, the distance of point (-7, -8) from O is 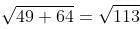 , which is more than 10.
, which is more than 10.
So, point (-7, -8) lies outside the given circle.
Hence, option (1) is correct.
Report a problem
Question for Practice Questions Level 2: Coordinate Geometry - 2
Try yourself:Find the equation of a straight line which contains the point 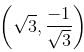 with inclination 150o.
with inclination 150o.
Explanation
Report a problem
Question for Practice Questions Level 2: Coordinate Geometry - 2
Try yourself:Find the point which divides the line joining the points A (1, 3) and B (2, 7) in the ratio of 3 : 4 externally.
Explanation
Report a problem
Question for Practice Questions Level 2: Coordinate Geometry - 2
Try yourself:If C is the centroid of the triangle PQR and the coordinates of points P, Q, R and C respectively are (x, 1), (0, y), (1/2, 0) and (1/2, 1/3), find the measure of angle PQR.
Explanation
The centroid of ΔPQR has coordinates (1/2, 1/3).
Therefore, 1/2 = (x + 0 + 1/2)/3 and 1/3 = (1 + y + 0)/3
So, x = 1 and y = 0
Angle PQR is equal to angle between line PQ and line QR.
Slope of PQ (m1)= (0 - 1)/(0 - 1) = 1
Slope of QR (m2)= (0 - 0)/((1/2) - 0) = 0
Angle between line PQ and line QR = tan θ = (m1 - m2)/(1 + m1m2) = (1 - 0)/(1 + (0)(1)) = 1
tan θ = 1
θ = 45°
Report a problem
Question for Practice Questions Level 2: Coordinate Geometry - 2
Try yourself:In the xy-plane, which of the following points is the greatest distance from the origin?
Explanation
The square of the distance from the origin of (x, y) is x2 + y2.
This values for the different points given in options are 9, (4 + 9), (1 + 9) and 9, respectively. Among these, 4 + 9 is the greatest.
Report a problem
Question for Practice Questions Level 2: Coordinate Geometry - 2
Try yourself:The projection (the foot of perpendicular) from (x, y) on the x-axis is
Explanation
The foot of perpendicular of a point on the x-axis always has abscissa equal to the perpendicular distance of the point from the y-axis and ordinate 0.
The projection or foot of perpendicular of (x, y) on the x-axis is (x, 0).
Report a problem
Question for Practice Questions Level 2: Coordinate Geometry - 2
Try yourself:If a, b and c are the sides of a triangle, and a2 + b2 + c2 = ab + bc + ca, then the triangle is
Explanation
a2 + b2 + c2 = ab + bc + ac
(a - b)2 + (b - c)2 + (c - a)2 = 0 ...(1)
Since the sum of squares is zero, each term should be zero.
⇒ (a - b)2 = 0, (b - c)2 = 0, (c - a)2 = 0
⇒ a = b = c
Hence, the triangle is equilateral.
Report a problem
Question for Practice Questions Level 2: Coordinate Geometry - 2
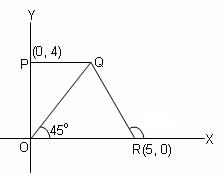
Try yourself:In the given figure, if PQ is parallel to OR, then what is the area of quadrilateral PQRO?
Explanation
Since ∠POR = 90° and ∠QOR = 45°, POQ is also equal to 45°.
So, ∠PQO = 45° and ∠QPO = 90°
Therefore, ΔQPO is an isosceles right-angled triangle.
So, OP = PQ = 4 units and OR = 5 units.
Now, OPQR is a trapezium with PQ and OR as its parallel sides.
So, area = ½(PQ + OR) × OP = ½ × (4 + 5) × 4 = 18 sq. units
Report a problem
Question for Practice Questions Level 2: Coordinate Geometry - 2
Try yourself:The point that divides the line joining the points (1, 2) and (3, 4) internally in the ratio of 1 : 1 lies in the
Explanation
Since the coordinates of both the points are positive, the line joining them lies in the first quadrant. The division of the line in the ratio of 1 : 1 means that the mid-point of this line also lies in the first quadrant, with both coordinates positive.
Report a problem
Question for Practice Questions Level 2: Coordinate Geometry - 2
Try yourself:The line (1 + K)X + (3 – K)Y = 2(1 + 3K) passes through a fixed point P for any value of K. Find the co-ordinates of P.
Explanation
(1 + K)X + (3 – K)Y = 2(1 + 3K)
Check the options.
Option (2): L.H.S. = (1 + K)(5) + (3 – K)(–1)
= 5 + 5K – 3 + K
= 2 + 6K
= 2(1 + 3K) = R.H.S.
Report a problem
Question for Practice Questions Level 2: Coordinate Geometry - 2
Try yourself:The vertices of a square S have coordinates (-1, -2), (-1, 1), (2, 1) and (2, -2). What are the coordinates of the point where the diagonals of S intersect?
Explanation
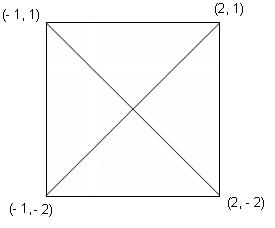
The diagonals of a square bisect each other.
So, the point at which the diagonals meet will be the midpoint of a line joining a pair of opposite vertices.
As can be seen from the figure, (-1, -2) and (2, 1) are opposite vertices.
Their midpoint has coordinates ((-1 + 2)/2, (-2 + 1)/2), or (1/2, -1/2).
Report a problem
Question for Practice Questions Level 2: Coordinate Geometry - 2
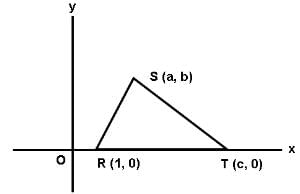
Try yourself:In the rectangular coordinate system shown below, the area of triangle RST is _______.
Explanation
x–coordinates of R and T are 1 and c, respectively. So, the length of RT = (c – 1).
Length of the altitude from S = Its distance from the x–axis = Its y–coordinate = b
So, the area of ΔRST = b(c – 1)/2
Report a problem
Question for Practice Questions Level 2: Coordinate Geometry - 2
Try yourself:The incentre of a triangle formed by the lines y = 0, 3x + 4y = 48 and 3y - 4x = 36 is
Explanation
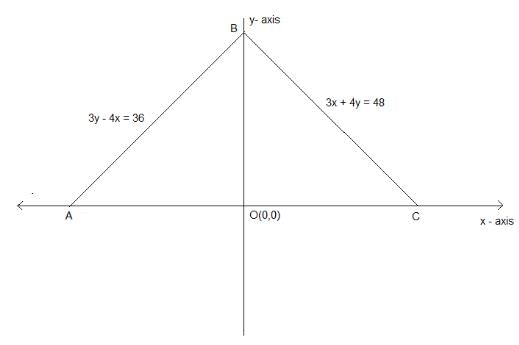
Point C(x3 ,y3) is the intersection of 3x + 4y = 48 with y = 0.
So, the coordinates of C are (16, 0).
Point A(x1 ,y1) is the intersection of 3y - 4x = 36 with y = 0.
So, the coordinates of A are (-9, 0).
Point B(x2 ,y2) is the intersection of 3x + 4y = 48 and 3y - 4x = 36.
So, the coordinates of B are (0, 12).
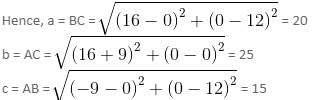
Coordinates of the incentre
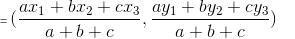
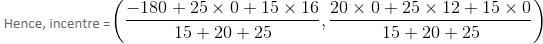
= (1, 5)
Report a problem
Question for Practice Questions Level 2: Coordinate Geometry - 2
Try yourself:Two points (a, 0) and (0, b) are joined by a straight line. Another point on this line is
Explanation
The equation of the line passing through (a, 0) and (0, b) is:
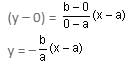
On putting the options, we get to know that option (1) is correct.
Report a problem
Question for Practice Questions Level 2: Coordinate Geometry - 2
Try yourself:If the coordinates of the centroid of a triangle are (2/3, 5/3) and the coordinates of two vertices of the triangle are (-1, 0) and (3, 0), then what are the coordinates of the third vertex of the triangle?
Explanation
Coordinates of centroid (G)
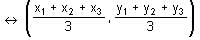
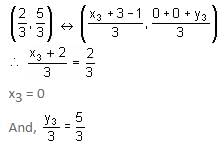
y3 = 5
∴ (x3, y3) = (0, 5)
Report a problem
Question for Practice Questions Level 2: Coordinate Geometry - 2
Try yourself:A line segment with end points A(-6, 10) and B(3, -8) is divided in the ratio 2 : 7 by a point P. Find the coordinates of point P.
Explanation
Report a problem
Question for Practice Questions Level 2: Coordinate Geometry - 2
Try yourself:If point (t, 1) is located inside the circle x2 + y2 = 10, then t must lie between
Explanation
As (t, 1) is located inside the given circle, its distance from the centre, i.e. origin, should be less than the radius, i.e. √10 units.
∴ Distance between (t, 1) and origin
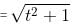
so,
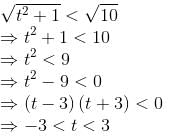
Report a problem
Question for Practice Questions Level 2: Coordinate Geometry - 2
Try yourself:Find the inclination and perpendicular distance of a line represented by (x/2) + (√3y/2) = 12√5 from the origin.
Explanation
Equation of the line (x/2) + (√3y/2) = 12√5 can also be written as:
x cos 60° + y sin 60° = 12√5
Comparing this with the normal form of equation, x cos θ + y sin θ = p, we get the inclination as 60° and the perpendicular distance from the origin as 12√5 units.
Report a problem

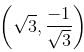 with inclination 150o.
with inclination 150o.



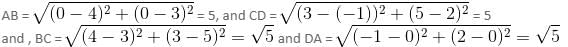
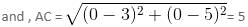
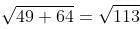 , which is more than 10.
, which is more than 10.