This EduRev document offers 10 Multiple Choice Questions (MCQs) from the topic Exponents & Logarithm (Level - 2). These questions are of Level - 2 difficulty and will assist you in the preparation of CAT & other MBA exams. You can practice/attempt these CAT Multiple Choice Questions (MCQs) and check the explanations for a better understanding of the topic.
Question for Practice Questions Level 2: Exponents & Logarithm - 1
Try yourself:If loga p = 2.3, the value of 3 loga 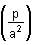 is
is
Explanation
3 loga p/a2)
= 3[loga p – loga a2] [∵ log m/n = log m – log n]
= 3[loga p – 2 loga a] [∵ log mn = n log m]
= 3[2.3 – 2 × 1] [∵ logm m = 1]
= 3 × 0.3
= 0.9
Report a problem
Question for Practice Questions Level 2: Exponents & Logarithm - 1
Try yourself:If 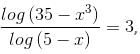 then the value of x could be
then the value of x could be
Explanation
log (35 - x3)/log (5 - x) = 3
⇒ log (35 - x3) = 3 log (5 - x)
⇒ (35 - x3) = (5 - x)3
i.e. 35 - x3 = 125 - x3 - 15x(5 - x)
⇒ 15x2 - 75x + 90 = 0
Or, 3x2 - 15x + 18 = 0
⇒ (3x - 9)(x - 2) = 0
⇒ Either x = 3 or x = 2
Report a problem
Question for Practice Questions Level 2: Exponents & Logarithm - 1
Try yourself:If log x3 + log 6a = log 162 + log a, find the value of x.
Explanation
log x3 = log 162 + log a - log 6a
= log [162a ÷ 6a]
= log 27
log x3 = log 27
i.e. x3 = 27
x = 3
Report a problem
Question for Practice Questions Level 2: Exponents & Logarithm - 1
Try yourself:If x3/7 = 423, the value of log x3 is
Explanation
Given: x3/7 = 423
On taking log of both the sides, the equation becomes:

It is nearest to 18.38.
So, option 3 is correct answer.
Report a problem
Question for Practice Questions Level 2: Exponents & Logarithm - 1
Try yourself:Find the solution of the equation log7 log5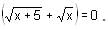
Explanation
Report a problem
Question for Practice Questions Level 2: Exponents & Logarithm - 1
Try yourself:What will you get after simplifying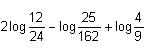 ?
?
Explanation
2log(12/24) - log(25/162) + log(4/9)
= 2log(1/2) - log25 + log162 + log4 - log9
= 2log1 - 2log2 - 2log5 + log(34 x 2) + 2log2 - log32
= -2log2 - 2log5 + 4log3 + log2 + 2log2 - 2log3
= 2log3 - 2log5 + log2
= log9 + log2 - log25
= log(9 × 2) - log25
= log18 - log25
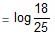
Hence, option (d) is correct.
Report a problem
Question for Practice Questions Level 2: Exponents & Logarithm - 1
Try yourself:The least value of the expression 2 log10 (x) - logx (0.01), for x > 1 is
Explanation
2log10 x - logx (0.01)
= 2log10 x - logx 10-2
= 2log10 x + 2logx 10
= 2[log10 x + logx 10] ≥ 2.2 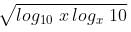 ≥ 4
≥ 4
As A.M. ≥ G.M. of two positive values.
Report a problem
Question for Practice Questions Level 2: Exponents & Logarithm - 1
Try yourself:Find the value of log10(tan 1°) + log10(tan 2°) + … + log10(tan 89°).
Explanation
log10(tan 1°) + log10(tan 2°) + log10(tan 3°) + … + log10(tan 88°) + log10(tan 89°)
= log10((tan 1°)(tan 89°)) + log10((tan 2°)(tan 88°)) + ... + log10(tan 45°)
= log10((tan 1°)(cot 1°)) + log10((tan 2°)(cot 2°)) + ... + log10(tan 45°)
= log10 1 + log10 1 + … + log10 1 = 0
Report a problem
Question for Practice Questions Level 2: Exponents & Logarithm - 1
Try yourself:If f(n) = log2 3 × log3 4 × log4 5 ….. logn – 1 n, then the value of 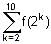 is
is
Explanation
Report a problem
Question for Practice Questions Level 2: Exponents & Logarithm - 1
Try yourself:The value of log2 3.log3 4.log4 5........ log98 99.log99 100 is
Explanation
By using base change formula:
log3 4 = (log2 4)/(log2 3)
log4 5 = (log2 5)/(log2 4)
...
log99 100 = (log2 100)/(log2 99)
Putting these values in the expression, we get the value of the expression as log2 100.
Hence, answer option c is correct.
Report a problem
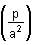 is
is
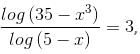 then the value of x could be
then the value of x could be
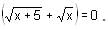
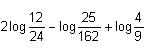 ?
?
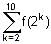 is
is


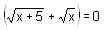
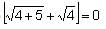

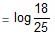
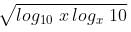 ≥ 4
≥ 4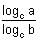 to rewrite f(n) in terms of logarithms to the base 2.
to rewrite f(n) in terms of logarithms to the base 2.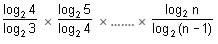 = log2 n
= log2 n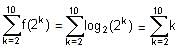 = 2 + 3 + 4 + ……. + 10 = 54
= 2 + 3 + 4 + ……. + 10 = 54













