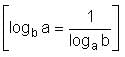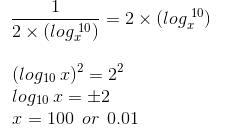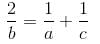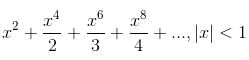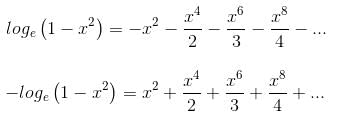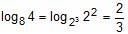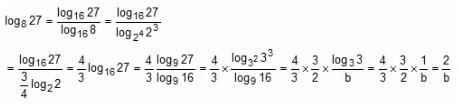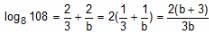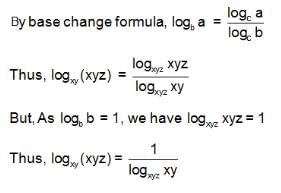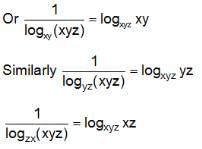This EduRev document offers 15 Multiple Choice Questions (MCQs) from the topic Exponents & Logarithm (Level - 2). These questions are of Level - 2 difficulty and will assist you in the preparation of CAT & other MBA exams. You can practice/attempt these CAT Multiple Choice Questions (MCQs) and check the explanations for a better understanding of the topic.
Question for Practice Questions Level 2: Exponents & Logarithm - 2
Try yourself:If x + 1/x = 3, then the value of 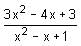 is
is
Explanation
Report a problem
Question for Practice Questions Level 2: Exponents & Logarithm - 2
Try yourself:If 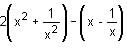 – 7 = 0, then two values of x are
– 7 = 0, then two values of x are
Explanation
Report a problem
Question for Practice Questions Level 2: Exponents & Logarithm - 2
Try yourself:Find the value of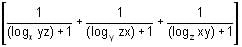 .
.
Explanation
Report a problem
Question for Practice Questions Level 2: Exponents & Logarithm - 2
Try yourself:Which of the following is true?
Explanation
log11 1650 = log11 (11 × 150) = log11 11 + log11 150 = 1 + log11 150
Now, as 112 = 121 and as 121 < 150, we have log11 150 > 2.
Thus, log11 1650 > 1 + 2.
Or, log11 1650 > 3
log13 1950 = log13 (13 × 150) = log13 13 + log13 150 = 1 + log13 150
Now, as 132 = 169 and as 169 > 150, we have log13 150 < 2.
Thus, log13 1950 < 1 + 2 or log13 1950 < 3.
⇒ log13 1950 < log11 1650
Hence, answer option a is correct.
Report a problem
Question for Practice Questions Level 2: Exponents & Logarithm - 2
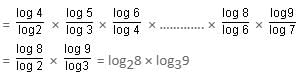
Try yourself:If x = log24 + log35 + log46 + log57 + log68 + log79, then which of the following is true?
Explanation
Report a problem
Question for Practice Questions Level 2: Exponents & Logarithm - 2
Try yourself:If1/3 log3 M + 3 log3 N = 1 + log0.008 5, then
Explanation
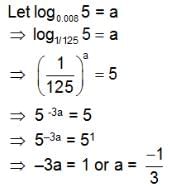
The given equation boils down to the following.
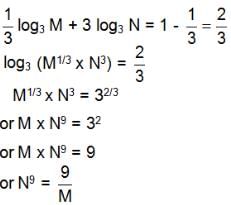
Hence, answer option b is correct.
Report a problem
Question for Practice Questions Level 2: Exponents & Logarithm - 2
Try yourself:If 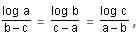 then find the value of aa bb cc.
then find the value of aa bb cc.
Explanation
Let 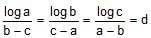
Thus, loga = (b - c)d; logb = (c - a)d; logc = d(a - b)
Now, let aabbcc = f
Or, log(aabbcc) = logf
Or, a loga + b logb + c logc = logf
Plugging in the valued of loga, logb & logc in terms of d in the above equation,
we get
a (b - c)d + b(c - a)d + c(a - b)d = logf
or 0 = log f
or, f = 1
∴ aabbcc = 1
Report a problem
Question for Practice Questions Level 2: Exponents & Logarithm - 2
Try yourself:If log10 x - log10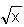 = 2 logx 10, then x is equal to
= 2 logx 10, then x is equal to
Explanation
Report a problem
Question for Practice Questions Level 2: Exponents & Logarithm - 2
Try yourself:If log (a + c), log (c - a), log (a - 2b + c) are in A.P, then
Explanation
log (a + c), log (c - a), log (a - 2b + c) are in A.P.
log (c - a) - log (a + c) = log (a - 2b + c) - log (c - a)

c2 + a2 - 2ac = a2 + c2 + 2ac - 2ab - 2bc
4ac = 2ab + 2bc
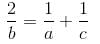
So, a, b, c are in H. P.
Report a problem
Question for Practice Questions Level 2: Exponents & Logarithm - 2
Try yourself:Arrange the following in descending order:
A = 1822, B = 2218, C = 2117
Explanation
A = 1822, B = 2218, C = 2117
We know that ab > ba, where a < b and a, b ≥ 3.
Thus, 1822 > 2218
Moreover, 1822 > 2218 > 2117
Thus, the required sequence is ABC. Hence, option (a) is correct.
Report a problem
Question for Practice Questions Level 2: Exponents & Logarithm - 2
Try yourself:The sum of the series x2 + 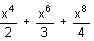 + ..., |x| < 1, is
+ ..., |x| < 1, is
Explanation
Report a problem
Question for Practice Questions Level 2: Exponents & Logarithm - 2
Try yourself:Find the value of x in log (x - 2) + log (x - 1) = log 20 - 1.
Explanation
The given equation is equivalent to:
log (x - 2)(x - 1) = log 20 - log 10
log (x - 2)(x - 1) = log 2
(x - 2)(x - 1) - 2 = 0
x2 - 3x + 2 - 2 = 0
x(x - 3) = 0
x = 0 or x = 3
x = 0 is not admissible since logarithm of a negative number (when used in the given equation) is not defined.
∴ x = 3
Report a problem
Question for Practice Questions Level 2: Exponents & Logarithm - 2
Try yourself:If log12 27 = a and log9 16 = b, then find log8 108.
Explanation
Report a problem
Question for Practice Questions Level 2: Exponents & Logarithm - 2
Try yourself: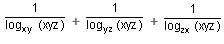 equals
equals
Explanation
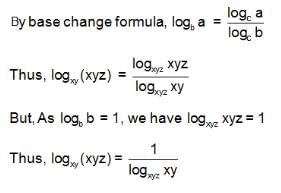
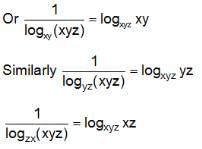
Thus, the expression becomes
logxyz xy + logxyz yz + logxyz xz
= logxyz (x2y2z2) = logxyz(xyz)2 = 2logxyz xyz = 2
Report a problem
Question for Practice Questions Level 2: Exponents & Logarithm - 2
Try yourself:Let u = (log2 x)2 - 6 log2 x + 12, where x is a real number. Then, the equation xu = 256 has
Explanation
u = (log2 x)2 - 6 log2 x + 12 & xu = 256 = 28 = 44 = 162 = 2561
If x = 2 ⇒ u = (log2 2)2 - 6 log2 2 + 12
u = 1 - 6 + 12 = 7 (Not possible)
If x = 4 ⇒ u = (log2 4)2 - 6 log2 4 + 12
= (2 log2 2)2 - 12 log2 2 + 12
= 4 - 12 + 12 = 4 (Possible)
If x = 16 ⇒ u = (log2 16)2 - 6 log2 16 + 12
u = 16 - 24 + 12
u = 4 (Not possible)
If x = 256 ⇒ u = (8 log2 2)2 - 48 log2 2 + 12
= 64 - 48 + 12
u = 28 (Not possible)
x can have exactly one solution.
Report a problem
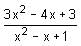 is
is
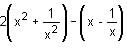 – 7 = 0, then two values of x are
– 7 = 0, then two values of x are
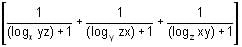 .
.
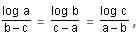 then find the value of aa bb cc.
then find the value of aa bb cc.
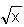 = 2 logx 10, then x is equal to
= 2 logx 10, then x is equal to
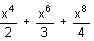 + ..., |x| < 1, is
+ ..., |x| < 1, is
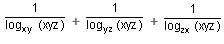 equals
equals

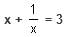
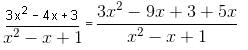
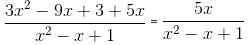
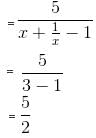
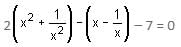
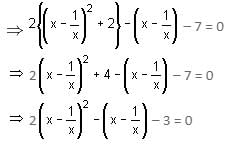
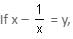
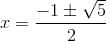
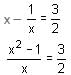
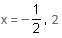
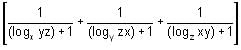
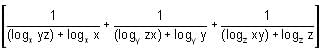
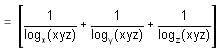
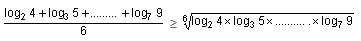
 ≥ 67/6.
≥ 67/6.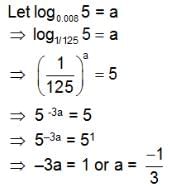
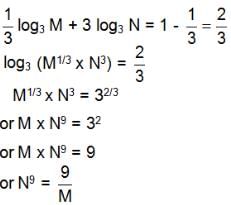
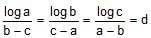
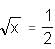 log10 x
log10 x log10 x = 2logx 10
log10 x = 2logx 10 log10 x = 2logx 10 … (i)
log10 x = 2logx 10 … (i)