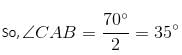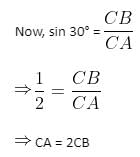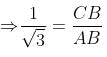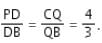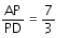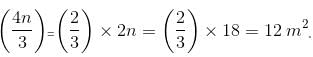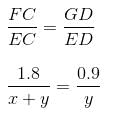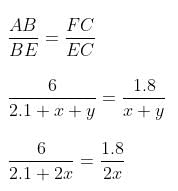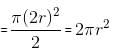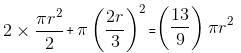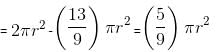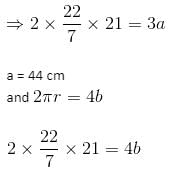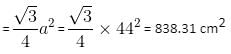This EduRev document offers 20 Multiple Choice Questions (MCQs) from the topic Geometry (Level - 2). These questions are of Level - 2 difficulty and will assist you in the preparation of CAT & other MBA exams. You can practice/attempt these CAT Multiple Choice Questions (MCQs) and check the explanations for a better understanding of the topic.
Question for Practice Questions Level 2: Geometry - 2
Try yourself:If segments AB, BC and CD subtend angles of 80°, 60° and 70°, respectively, at the centre O of a circle, then the measure of an acute angle between AC and BD would be _____.
Explanation
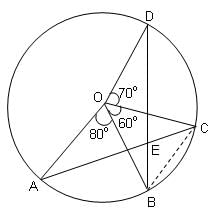
As shown in the figure, the required acute angle is $\displaystyle \angle$AEB.
∠ACB = 1/2(∠AOB) = (1/2)(80°) = 40°
[∵ the angle subtended by an arc or a chord of a circle at the centre is double the angle subtended by it at any point on the remaining part of the circle.]
Similarly:
∠DBC = (1/2)(∠DOC) = (1/2)(70°) = 35°
∴ ∠AEB = ∠ECB + ∠EBC =∠ACB +∠DBC [∵ ∠AEB is the exterior angle of ΔBEC.]
= 40° + 35° = 75°
Report a problem
Question for Practice Questions Level 2: Geometry - 2
Try yourself:In the given figure, O is the centre of the circle, ∠BOC = 70° and AB is perpendicular to OC. Find the measure of angle OCA.
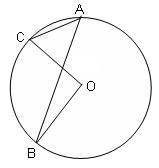
Explanation
We know that the angle made by a chord at the centre is twice that made by it at any point on the circle.
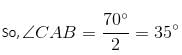
It is also given that AB is perpendicular to OC. Let us suppose they intersect at M.
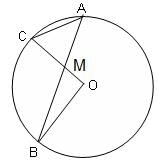
Now, in triangle AMC:
∠AMC + ∠ACM + ∠CAM = 180°
i.e.
90° + 35° + ∠ACM = 180°
∠ACM = 180° - 125° = 55°
∠ACM = ∠ACO
So, ∠OCA = 55°
Report a problem
Question for Practice Questions Level 2: Geometry - 2
Try yourself:What is the smallest possible radius of a circle such that it is possible to place 6 points on its circumference with an integral distance between any two adjacent points?
Explanation
The smallest radius means the smallest circumference. The circumference is 2πr. For six equidistant points with distance between them to be an integer, this integer has to be the smallest, i.e. 1. Therefore, the circumference is 6 units.
So, 2πr = 6 or r = 3/π.
Report a problem
Question for Practice Questions Level 2: Geometry - 2
Try yourself:In the given figure, AB is a diameter of the circle, line BC is tangent to the circle, ∠BAC = 30° and length of CD = √3 units. Find the radius of the circle.
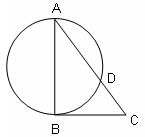
Explanation
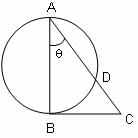
In ΔACB, ∠BAC = θ = 30°
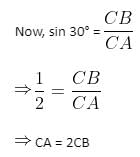
As AB is a diameter, CB2 = CD.CA.
Thus, CB2 = 2CD.CB, which implies CB = 2.CD =2√3
Again, in ΔACB, ∠BAC = θ = 30°, so tan 30° = CB/AB
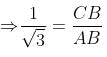
We obtain, AB = √3 x CB = √3 x 2√3 = 6
Hence, radius of the circle = 6/2 = 3 units
Option 1 is the answer.
Report a problem
Question for Practice Questions Level 2: Geometry - 2
Try yourself:What is the perimeter of triangle ABC?
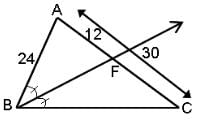
Explanation
Now, from the property of angle bisector theorem, an angle bisector divides opposite sides in the same ratio as the side containing the angle.

Perimeter of ΔABC = AB + BC + CA = 24 + 36 + 30 = 90 units
Report a problem
Question for Practice Questions Level 2: Geometry - 2
Try yourself:ABCDE is a regular pentagon inscribed in the given circle. What is the measure of the acute angle θ between AC and BD?

Explanation
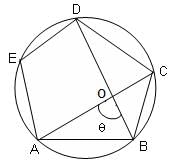
We know that ABCDE is a regular pentagon.
Therefore, all its sides are equal and each angle measures 108°.
Now, in ΔBCD, ∠BCD = 108°
∴ ∠BDC = ∠DBC = 36°
Similarly, in ΔABC, ∠BAC = $%5Cangle$ACB = 36°
∴ ∠AOB = θ = ∠DBC + ∠ACB = 36° + 36° = 72° {∵ ∠AOB is the exterior angle of ΔOBC}
Report a problem
Question for Practice Questions Level 2: Geometry - 2
Try yourself:In the given figure, if AC is a diameter of the circle and the angles CAD, BAC, BCA and ACD form an arithmetic progression with angle CAD = 15°, then which of the following options is the measure of angle BCA?
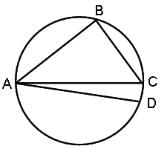
Explanation
In cyclic quadrilateral ABCD, ∠CAD + ∠BAC + ∠BCA + ∠ACD = 180° and these angles form an AP with the first term equal to 15°.
15 + 15 + d + 15 + 2d + 15 + 3d = 180
6d = 120
d = 20
Hence, the common difference is 20° and ∠BCA = 15 + 2d = 55°.
Report a problem
Question for Practice Questions Level 2: Geometry - 2
Try yourself:A tangent to a circle of radius 3 cm from an external point P is of length 4 cm. Find the shortest distance of point P from a point on the circumference of the circle.
Explanation
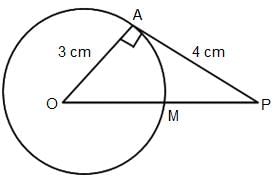
Given above is the figure based on the data provided in the question.
In triangle OAP,
OP2 = 32 + 42
OP = 5 cm
Also, OP = OM + MP
So, MP = (5 - 3) cm = 2 cm
Report a problem
Question for Practice Questions Level 2: Geometry - 2
Try yourself:Three circles, each with a radius of 10 cm, are drawn tangent to one another so that their centres are all in a straight line. These circles are inscribed in a rectangle which is inscribed in another circle. The area of the largest circle is ________.
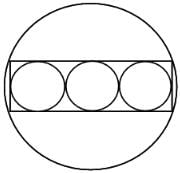
Explanation
By symmetry, the centre of the largest circle is the centre of the smaller circle in the middle. By making the constructions as shown and with appropriate representation of the lengths, we get r2 = 302 + 102 = 1000. Thus, A = πr2 = π(1000) = 1000π cm2.
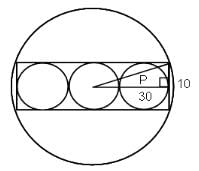
Report a problem
Question for Practice Questions Level 2: Geometry - 2
Try yourself:In the figure, ABCDEF is a regular hexagon and ∠AOF = 90°. FO is parallel to ED. What is the ratio of the area of the triangle AOF to that of the hexagon ABCDEF?
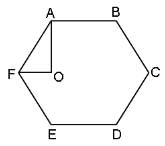
Explanation
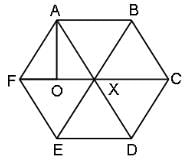
After joining all the opposite vertices (let them meet at point X), we find that right triangle AOF ≌ Right triangle AOX.
⇒ Area of ΔAOX = Area of ΔAOF

Report a problem
Question for Practice Questions Level 2: Geometry - 2
Try yourself:In the figure (not drawn to scale), P is a point on AB such that AP : PB = 4 : 3. PQ is parallel to AC and QD is parallel to CP. In ΔARC, ∠ARC = 90° and in ΔPQS, ∠PSQ = 90°. The length of QS is 6 cm. What is the ratio of AP : PD?

Explanation
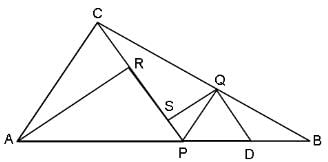
According to the given information, AP/PB =4/3
PQ || AC and QD || CP.
Triangles ABC and PBQ are similar (by AAA).
Therefore,
CQ/QB = 4/3
Similarly, triangles PBC and DBQ are similar and 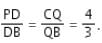
If AP = 4x and PB = 3x, then DB = 9x/7 and PD = 12x/7
So,
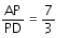
Report a problem
Question for Practice Questions Level 2: Geometry - 2
Try yourself:In the figure given below, AB is a diameter of the circle, TD is a tangent to the circle and AB = 2AD. If AHD = 36° and DBA = 30°, then what is the measure of CDT?
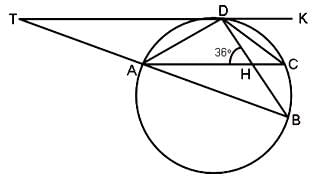
Explanation
∠BDA = 90°, ∠AHD = 36°, AB = 2AD
∠DBA = 30°
So, DCA = 30° (because angles by the same segment at the circumference are equal)
Now, we know that triangle ABD is a right triangle.
So, ∠DAB = 60° and∠DBA = 30°
∠TDA =∠DBA (Angles in alternate segment)
Report a problem
Question for Practice Questions Level 2: Geometry - 2
Try yourself:What is the maximum number of dogs that can be tied in a spherical hall such that all the dogs are equidistant from each other?
Explanation
Let the dogs be tied at P, Q, R and S, where P, Q and R are in one plane, and S is in a different plane.
Note: PS = QS = RS = PQ = QR = RS
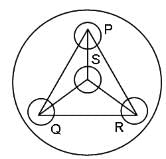
ΔPQS, ΔPSR and ΔQSR are congruent and equilateral.
Report a problem
Question for Practice Questions Level 2: Geometry - 2
Try yourself:In the diagram given below,
∠ABC = 90° = ∠DCH = ∠DOE = ∠EHK = ∠FKL = ∠GLM = $∠LMN
AB = BC = 2CH = 2CD = EH = FK = 2HK = 4KL = 2LM = MN
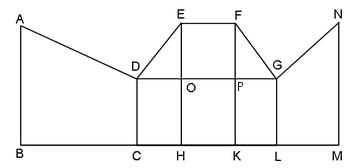
What is the measure of ∠FGO?
Explanation
According to the given condition, AB = 2CD.
⇒ KP = CD = PF = AB/2
Also, AB = 4KL
⇒ KL = PG = AB/4
Now, in the right triangle FPG,
tan (∠FGO) = PF/PG = 2
So, none of the options is satisfying the above equation.
Report a problem
Question for Practice Questions Level 2: Geometry - 2
Try yourself:In the figure (not drawn to scale), A, B and C are three points on a circle with centre O. The chord BA is extended to a point T, such that CT becomes a tangent to the circle at point C. If ∠ATC = 30° and ∠ACT = 50°, find the measure of angle ∠BOA.
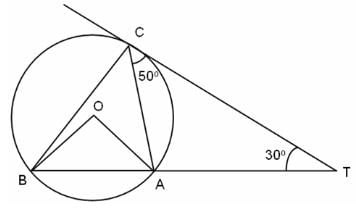
Explanation
According to the given information: ∠CAT = 100° and ∠BAC = 80°
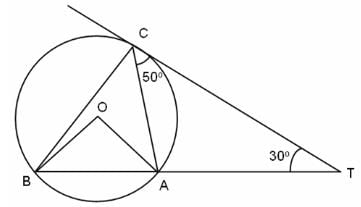
∠ABC = 50° = ∠ACT ( Angles are in the alternate segment)
∠BCA = 180° - (80° + 50°) = 180° - 130° = 50°
Hence, ∠BOA = 2 x∠BCA = 100°
Report a problem
Question for Practice Questions Level 2: Geometry - 2
Try yourself:The bisectors of the four angles of a parallelogram are drawn. An acute angle of the parallelogram is 60° and the adjacent sides are 8 and 6 units. What is the area of the quadrilateral whose vertices are the points of intersection of the bisectors?
Explanation
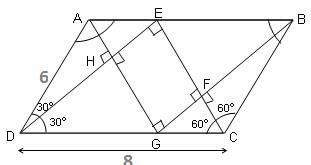
An acute angle of the parallelogram is 60° (given).
Therefore, ∠ADC and ∠ABC = 60°
Thus, ∠BAD and ∠BCD = 120°
EFGH forms a rectangle in the above given figure.
Consider ΔDEC, DC = 8, EC = 4 and ED = 4√3 (By 30°, 60°, 90° theorem)
Considering ΔBFC, BC = 6, FC = 3 and FB = 3√3 (By 30°, 60°, 90° theorem)
Considering ΔAHD, AD = 6; therefore, AH = 3 and DH = 3√3
Now, side of the rectangle, EH = DE – DH = 4√3 – 3√3 = √3 and EF = EC – FC = 4 – 3 = 1
Area of rectangle EFGH = √3 square units
Report a problem
Question for Practice Questions Level 2: Geometry - 2
Try yourself:Let E be the midpoint of median AD of ABC. Let DB be produced to P, such that DB = BP and let DC be produced to Q, such that DC = CQ. Let EP cuts AB at L and EQ cuts AC at M. What is the area of pentagon BLEMC, if area of ABC is 18 m2?
Explanation
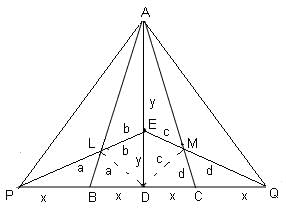
Join AP & AQ.
Now, let Area of ΔABC = 2n
Area of ΔABD = Area of ΔADC = 1/2 Area of ΔABC = n
As PD = BC = DQ;
Area of ΔAPD = Area of ΔABC = Area of ΔADQ = 2n
Area of ΔPED = Area of ΔPAE = 1/2 Area of ΔPAD = n
Similarly, Area of ΔEDQ = Area of ΔQEA = 1/2 Area of ΔQDA = n
Now,
Area of ΔLPB = Area of ΔLBD = a; Area of ΔLDE = Area of ΔLEA = b;
Area of ΔMDC = Area of ΔMQC = d; Area of ΔAEM = Area of ΔEDM = c
Area of ΔPDE = 2a + b = n
Area of ΔABD = 2b + a = n
Solving above two equations; we get, a = b = (n/3)
Similarly; we get c = d = (n/3)
Area of pentagon = a + b + c + d =
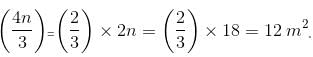
Report a problem
Question for Practice Questions Level 2: Geometry - 2
Try yourself:A father and his son were waiting at a bus stop in the evening. There was a lamp post behind them. The lamp post, the father and his son stood on the same straight line. The father observed that the shadows of his head and his son's head were incident at the same point on the ground. If the heights of the lamp post, the father and his son were 6 m, 1.8 m and 0.9 m, respectively, and the father was standing 2.1 m away from the post, then how far (in m) was the son standing from his father?
Explanation
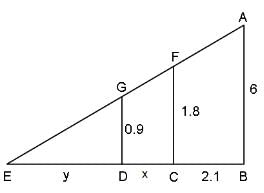
In ΔEDG and in ΔFEC:
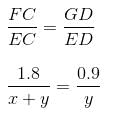
1.8y = 0.9x + 0.9y
0.9y = 0.9x
x = y
Now, in ΔABE and ΔFCE:
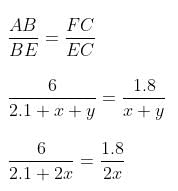
12x = 3.78 + 3.6x
8.4x = 3.78
x = 0.45 m
Report a problem
Question for Practice Questions Level 2: Geometry - 2
Try yourself:Three horses are grazing within a semi-circular field as shown in the diagram and AB is the diameter of the semi-circular field with centre at O. The horses are tied up at P, R and S such that PO and RO are the radii of semicircles with centres at P and R, respectively and S is the centre of the circle touching the two semi-circles with diameters AO and OB. The horses tied at P and R can graze within the respective semi-circles and the horse tied at S can graze within the circle centred at S. What is the percentage of area of the semi-circle with diameter AB that cannot be grazed by the horses?
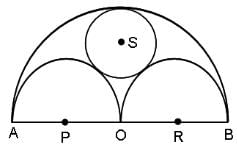
Explanation
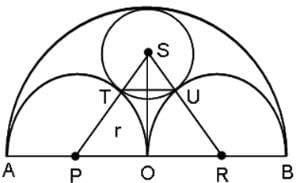
We can see that OP = OR
Suppose ST = y and PT = r
then SU = ST = y and PO = RO = RU = PT = r
So, RS = r + y and OS = 2r - y
In right angle ΔSOR
OS2 + OR2 = RS2
⇒ (2r - y)2 + r2 = (r + y)2
⇒ 4r2 + y2 - 4ry + r2 = r2 + y2 + 2ry
⇒ 4r2 - 4ry = 2ry

Area of the bigger semi-circular field
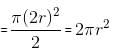
Total area of the grazing surface for horses =
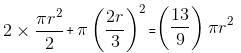
Then the non-grazing part of the field
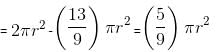
Report a problem
Question for Practice Questions Level 2: Geometry - 2
Try yourself:The circumference of a circle equals the perimeter of a triangle of equal sides and also the perimeter of a square. The areas covered by the circle, the triangle and the square are c, t and s, respectively. Which of the following relations is true?
Explanation
2πr = 3a = 4b (where r is the radius of the circle, a is the side of the triangle and b is the side of the square).
Now, take any values of r, a and b, which satisfy the given equation.
Let r = 21 cm,
Therefore, 2πr = 3a
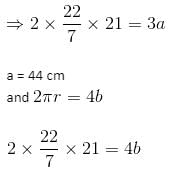
b = 33 cm
Therefore, area of circle =πr2 = (22/7) x 441 = 1386 cm2
Area of triangle
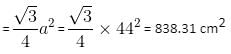
Area of square = b2 = 332 = 1089 cm2
In each case, one will find that: Area of circle > Area of square > Area of triangle
Or c > s > t
Report a problem