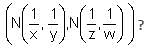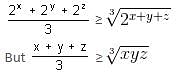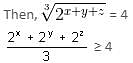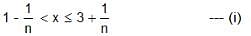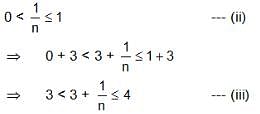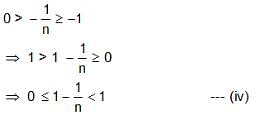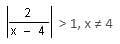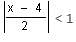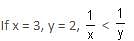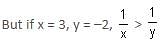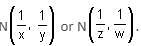This EduRev document offers 10 Multiple Choice Questions (MCQs) from the topic Inequalities (Level - 2). These questions are of Level - 2 difficulty and will assist you in the preparation of CAT & other MBA exams. You can practice/attempt these CAT Multiple Choice Questions (MCQs) and check the explanations for a better understanding of the topic.
Question for Practice Questions Level 2: Inequalities - 1
Try yourself:What values of 'x' satisfy the inequality x2/3 + x1/3 - 2 ≤ 0?
Explanation
x2/3 + x1/3 - 2 ≤ 0
Or (x1/3 - 1)(x1/3 + 2) ≤ 0
Or -8 ≤ x ≤ 1
Report a problem
Question for Practice Questions Level 2: Inequalities - 1
Try yourself:If f(x) = x3 - 4x + p and f(0) and f(1) have opposite signs, then which of the following is necessarily true?
Explanation
f(0) = p and f(1) = p - 3
Since f(0) and f(1) have opposite signs, so if p < 0, then p - 3 > 0, i.e. p > 3, which is not possible.
Or, p > 0 and p - 3 < 0
⇒ p < 3
⇒ 0 < p < 3
Hence, answer option 2 is correct.
Report a problem
Question for Practice Questions Level 2: Inequalities - 1
Try yourself:a2 + b2 is always
Explanation
As (a - b)2 is never negative.
a2 + b2 - 2ab is greater than or equal to zero.
Therefore, we can say that a2 + b2 ≥ 2ab.
Report a problem
Question for Practice Questions Level 2: Inequalities - 1
Try yourself:If xyz = 8, then what is the minimum value of 2x + 2y + 2z?
Explanation
Since AM ≥ GM,

x + y + z ≥ 6
To get minimum value, take x + y + z = 6.

⇒ 2x + 2y + 2z ≥ 12
Minimum value = 12
Report a problem
Question for Practice Questions Level 2: Inequalities - 1
Try yourself:How many pairs of natural numbers at (x, y) satisfy the inequality 3x + 5y < 20?
Explanation
(x, y) pairs satisfying the condition are (1, 1), (1, 2), (1, 3), (2, 1), (2, 2), (3, 1), (3, 2) and (4, 1).
So, total 8 pairs are there.
Report a problem
Question for Practice Questions Level 2: Inequalities - 1
Try yourself:|x| ≤ 2 and |y + 3| ≤ 5. What is the minimum possible value of x + y?
Explanation
|x| ≤ 2 ⇒ minimum value of x = - 2.
|y + 3| ≤ 5 ⇒ minimum value of y = - 8.
So, x + y = - 2 - 8 = - 10.
Report a problem
Question for Practice Questions Level 2: Inequalities - 1
Try yourself:Which of the following inequalities best describes a real number x, satisfying  for every positive integer n?
for every positive integer n?
Explanation
Report a problem
Question for Practice Questions Level 2: Inequalities - 1
Try yourself:What values of x satisfy  > 1, x ≠ 4?
> 1, x ≠ 4?
Explanation
Report a problem
Question for Practice Questions Level 2: Inequalities - 1
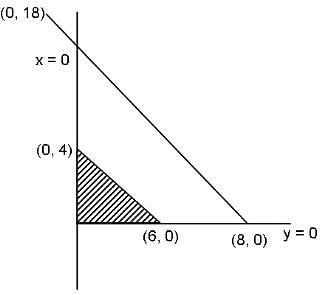
Try yourself:How many whole number pairs satisfy both the inequalities 2x + 3y ≤ 12 and 9x + 4y ≤ 72?
Explanation

The common part is x ≥ 0, y ≥ 0, 2x + 3y ≤ 12.

Total = 19
Report a problem
Question for Practice Questions Level 2: Inequalities - 1
Try yourself:If x > y > z > w, M (a, b) = maximum of a and b, and N (a, b) = minimum of a and b, then what is the value of M

Explanation
Report a problem
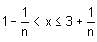 for every positive integer n?
for every positive integer n?
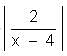 > 1, x ≠ 4?
> 1, x ≠ 4?