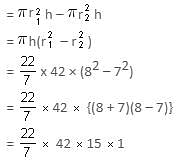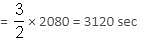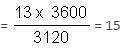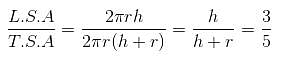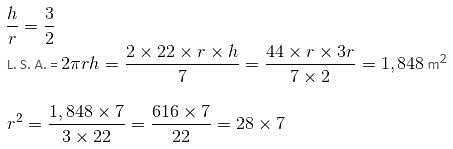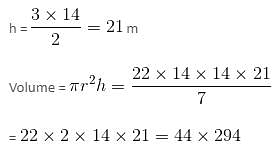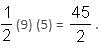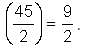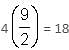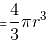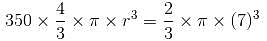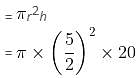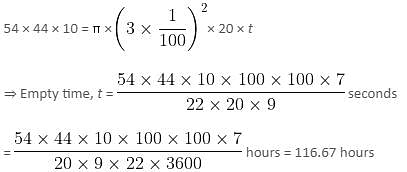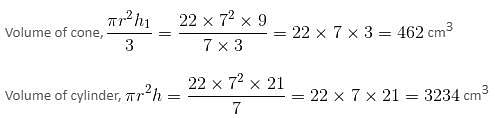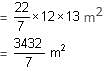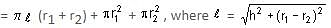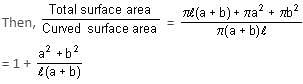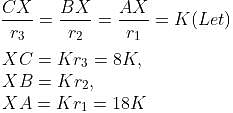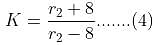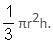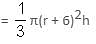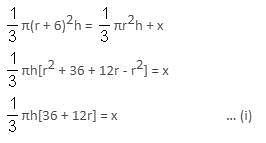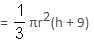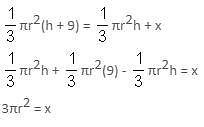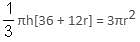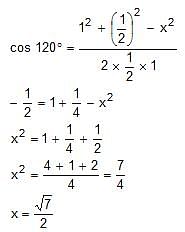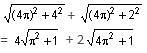This EduRev document offers 20 Multiple Choice Questions (MCQs) from the topic Mensuration (Level - 2). These questions are of Level - 2 difficulty and will assist you in the preparation of CAT & other MBA exams. You can practice/attempt these CAT Multiple Choice Questions (MCQs) and check the explanations for a better understanding of the topic.
Question for Practice Questions Level 2: Mensuration - 2
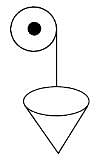
Try yourself:In the given diagram, a rope is wound around a circular drum whose diameter is 70 cm and a bucket is tied to the other end of the rope. Find the number of revolutions made by the drum if the bucket is to be raised by 11 m.

Explanation
Here, the height through which the bucket is to be raised = Number of revolutions of the drum × circumference

Report a problem
Question for Practice Questions Level 2: Mensuration - 2
Try yourself:One of the base edges of a metallic plate, which is in the form of a right-angled triangle, is soldered to a wire. The wire is rotated around its own axis. What is the maximum volume of the shape obtained by rotating the metallic plate, given that the smallest side of the triangular plate is 8 cm in length and the largest side is 2 cm greater than the second largest side?
Explanation
The figure formed on rotating a right-angled triangle is a right circular cone. First of all, we have to calculate its dimensions.
As shown in the adjoining figure, let the given dimensions of the right-angled triangle be x, x + 2 and 8.
(x + 2)2 = x2 + (8)2
⇒ x2 + 4 + 4x = x2 + (8)2
⇒ 4x = 60
⇒ x = 15
Report a problem
Question for Practice Questions Level 2: Mensuration - 2
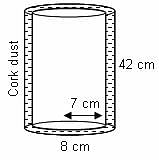
Try yourself:A cylindrical vessel of diameter 14 cm and height 42 cm is fixed symmetrically inside a similar vessel of diameter 16 cm and height 42 cm. If the total space between the two vessels is filled with cork dust for heat insulation purposes, then how many cubic centimetres of cork dust will be required?

Explanation
Height of the cylinders = 42 cm
Radius of the outer cylinder = r1 = 16/2 = 8 cm
Radius of the inner cylinder = r2 = 14/2 = 7 cm
Therefore, volume of the cork dust required = Volume of the outer cylinder – Volume of the inner cylinder

= 1980 cm3
Report a problem
Question for Practice Questions Level 2: Mensuration - 2
Try yourself:A tap drips at an average rate of 2 drops in 3 seconds. It takes 2080 drops of water to completely fill a hemispherical vessel of radius 8.3 cm. How many times can the vessel be filled in this manner in 13 hours?
Explanation
Average rate of tap = 2/3 drops/sec
Total number of drops in the completely filled vessel = 2080
So, time taken by the tap to drip 2080 drops 
i.e. Time required to fill the vessel = 3120 sec
∴ Number of times that the vessel be filled in this manner in 13 hours

Report a problem
Question for Practice Questions Level 2: Mensuration - 2
Try yourself:Ratio between the lateral surface area and the total surface area of a right circular cylinder is 3 : 5. If the lateral surface area is 1848 sq. m, then volume of the cylinder is (in cubic m).
Explanation
Report a problem
Question for Practice Questions Level 2: Mensuration - 2
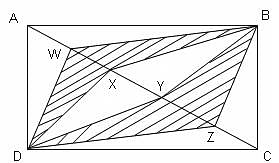
Try yourself:The given rectangle ABCD has length 9 and width 5. Diagonal AC is divided into 5 equal parts at W, X, Y and Z. Find the area of the shaded region.

Explanation
Report a problem
Question for Practice Questions Level 2: Mensuration - 2
Try yourself:If 350 stones of spherical shape are dropped into a hemispherical cup containing some water, they get fully submerged. Diameter of the cup is 14 m. What will be the radius of the stone, if the water just spills off from the hemispherical cup?
Explanation
Report a problem
Question for Practice Questions Level 2: Mensuration - 2
Try yourself:Find the approximate time taken to fill a chemical conical vessel, if the flow rate is 20 meters per minute from a cylindrical pipe whose diameter is 5 meters. Take diameter and depth of the conical vessel as 80 meters and 48 meters, respectively.
Explanation
Report a problem
Question for Practice Questions Level 2: Mensuration - 2
Try yourself:A rectangular reservoir has dimensions 54 meters × 44 meters × 10 meters. An outlet pipe of circular cross-section has a radius of 3 centimeters and the water runs through the pipe at a rate of 20 meters/second. What is the time taken by the outlet pipe to empty the reservoir full of water?
Explanation
Volume of water in the reservoir = Area of cross-section of pipe × Empty rate × Empty time
Let the empty time be t.

Report a problem
Question for Practice Questions Level 2: Mensuration - 2
Try yourself:Two cubes, each of edge length 6 cm, are joined end to end. The surface area of the resulting cuboid is
Explanation
The resulting cuboid has dimensions:
ℓ = (6 + 6) cm = 12 cm
b = 6 cm
h = 6 cm
Therefore, surface area of the cuboid
= 2(ℓb + bh + hℓ)
= 2[12 × 6 + 6 × 6 + 6 × 12] cm2 = 360 cm2

Report a problem
Question for Practice Questions Level 2: Mensuration - 2
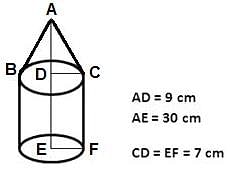
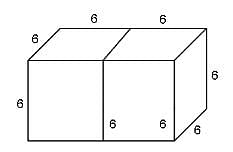
Try yourself:What is the volume (in cubic cm) of given figure?

Explanation
Volume of given figure = Volume of cone + Volume of cylinder
Radius of cone = Radius of cylinder, r = 7 cm
Height of cone = h1 = 9 cm
Height of cylinder, h = 30 - 9 = 21 cm

Volume of figure = 462 + 3234 = 3696 cm3
Report a problem
Question for Practice Questions Level 2: Mensuration - 2
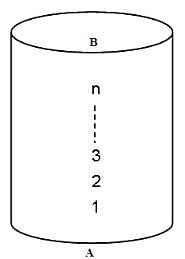
Try yourself:Consider a cylinder of height h cm and radius r = 2/π cm, as shown in the figure (not drawn to scale). A string of a certain length, when bound on its cylindrical surface starting at point A and ending at point B, gives a maximum of n turns (in other words, the string's length is the minimum length required to wind n turns). What is the vertical spacing in cm between the two consecutive turns?

Explanation
Total height = h
Number of turns = n
∴ Vertical spacing = h/h
Report a problem
Question for Practice Questions Level 2: Mensuration - 2
Try yourself:A solid is in the form of a cylinder with hemispherical ends. The total height of the solid is 19 cm and the diameter of the cylinder is 7 cm. The surface area of the solid is
Explanation
Radius of the hemisphere = Radius of the cylinder = Height of the hemisphere = 3.5 cm
Height of the cylinder = Total height - 2 × (Radius of the hemisphere)
Height of the cylinder = 19 cm - 7 cm = 12 cm
Radius of the hemisphere = 3.5 cm
Surface area of the solid = Surface area of the cylinder + 2 × (Surface area of the hemisphere)
= (2πrh) + 2 × (2πr2)
= (2 × (22/7) × 3.5(12 + 7)) cm2 = 22 × 19 sq. cm = 418 cm2
Report a problem
Question for Practice Questions Level 2: Mensuration - 2
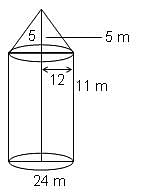
Try yourself:A tent is in the form of a right circular cylinder surmounted by a cone. The diameter of the cylinder is 24 m. The height of the cylindrical portion is 11 m, while the vertex of the cone is 16 m above the ground. What is the area of the curved surface for the conical portion?

Explanation
Radius of cone = 12 m
Height of cone = 5 m
Hence, slant height =

ℓ = 13 m
Curved surface area of cone = π rl

Report a problem
Question for Practice Questions Level 2: Mensuration - 2
Try yourself:Let ℓ be the slant height of a frustum. If a and b represent the two base radii, which of the following expressions represents the ratio of the total surface area to the curved surface area of the frustum?
Explanation
Report a problem
Question for Practice Questions Level 2: Mensuration - 2
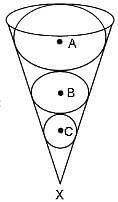
Try yourself:Three spherical marbles are placed in a hollow inverted cone, one above the other. Each marble is in contact with the adjacent marble(s). Also, each marble is in contact with the wall of the cone. The smallest marble has a radius of 8 cm. The largest marble has a radius of 18 cm.
The radius of the middle marble is
Explanation

Let X be the vertex of the cone and let CX = P, r3 = 8 cm, r1 = 18 cm.
Let A, B and C be the centres of largest, middle and smallest spheres.
Let their radii be r1 (largest), r2 (middle) and r3 (smallest), such that
XC = P ... (1)
XB = P + r3 + r2..(2)
AX = P + r3 + 2r2 + r1 ... (3)
Applying rule of similarity triangle, we have

From equation (2) we get,

From equation (3) we get,
5K = 13 + r2........ (5)
Solving equation (4) and equation (5), we get r2 = 12 cm
Report a problem
Question for Practice Questions Level 2: Mensuration - 2
Try yourself:Increasing the height of a cone by 9 units increases its volume by x cubic units. Increasing its radius by 6 units also increases its volume by x cubic units. If the original height is 3 units, then the original radius is _____.
Explanation
Report a problem
Question for Practice Questions Level 2: Mensuration - 2
Try yourself:A sealed bottle, which contains water, has been constructed by attaching a cylinder of radius 1 cm to a cylinder of radius 3 cm, as shown in Figure A. When the bottle is upright, the height of the water is 20 cm, as shown in the cross section of the bottle in Figure B. When the bottle is upside down, the height of the liquid is 28 cm, as shown in Figure C. What is the total height (in cm) of the bottle?

Explanation
We'll start by denoting the height of the large cylinder by h1 and the height of the small cylinder by h2. For simplicity, we'll suppose x = h1 + h2.
If the bottom cylinder is completely filled and the top cylinder is only partially filled, the top cylinder will have a cylindrical space that is not filled. This cylindrical space will have a height equal to x - 20 and a volume equal to π(1)2(x - 20).
Similarly, if we turn the bottle upside down, there will be cylindrical space unfilled that will have a height equal to x - 28 and a volume equal to π(3)2(x - 28).
Since these two unoccupied spaces must be equal, we can write:
π(1)2(x - 20) = π(3)2(x - 28)
x - 20 = 9x - 252
8x = 232
x = 29
Therefore, the total height is 29 cm.
Report a problem
Question for Practice Questions Level 2: Mensuration - 2
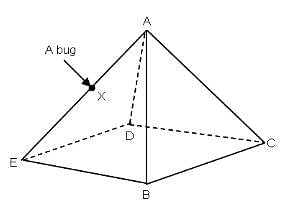
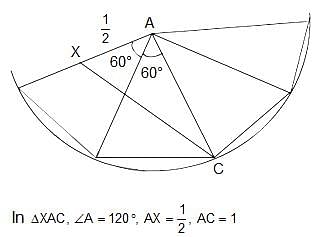
Try yourself:A certain pyramid has a square base with side 1 cm and four lateral faces, each of which is an equilateral triangle. A bug sitting at point X wishes to crawl over the faces of the pyramid to reach point C. Assuming that point X is half way up the pyramid, what is the length of the shortest trip he can take?

Explanation
Opening the pyramid, you will get

According to cosine formula,

Report a problem
Question for Practice Questions Level 2: Mensuration - 2
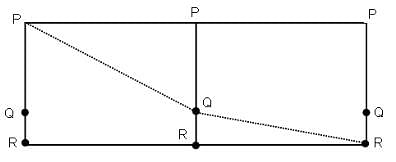
Try yourself:A cylindrical tank is 6 feet tall and its base is 4 feet in diameter. A bug crawls from a point P on the upper rim of the tank to a point Q which is directly 4 feet below P, going around the tank once in doing so. Then, the bug crawls from point Q to a point R, directly below P, on the bottom rim of the tank (the vertical distance from Q to R is 2 feet), again going around the can once in doing so. What is the length (in inches) of the shortest path that the bug could have taken from P to R?

Explanation
We cut the can along a line passing through P, Q and R, and we stretch out the tank so that its side is in the shape of a rectangle. Then, P, Q and R appear as points on two opposite edges of the rectangle. The length of the rectangle is 2π × 2 = 4π and its height is 6. We draw two such rectangles beside each other and indicate where P, Q and R lie along the edges, as shown below.

The shortest path from P to Q to R is indicated above (the first time around the tank is indicated by the line segment from P to Q, and the second time around the tank is indicated by the line segment from Q to R). Given that the vertical distance from P to Q is 4 feet and the vertical distance from Q to R is 2 feet, we get from two applications of the Pythagorean theorem that the length of the shortest path is

Report a problem