This EduRev document offers 15 Multiple Choice Questions (MCQs) from the topic Mixtures & Alligations (Level - 2). These questions are of Level - 2 difficulty and will assist you in the preparation of CAT & other MBA exams. You can practice/attempt these CAT Multiple Choice Questions (MCQs) and check the explanations for a better understanding of the topic.
Question for Practice Questions Level 2: Mixtures & Alligations - 2
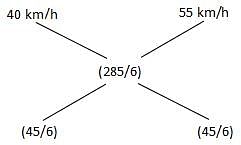
Try yourself:A bus driver is driving a bus at a speed of 40 km per hour. After travelling at this speed for some time, he increases its speed to 55 km per hour. If he travels a total distance of 285 km and the total time taken for the journey is 6 hours, then how much distance does he travel at the speed of 55 km per hour?
Explanation
Total distance travelled = 285 km
Total time taken = 6 hours
Average speed of journey = 285/6 km/h
By alligation method,

Therefore, the ratio of time spent travelling at 40 km/h to that travelling at 55 km/h =
Total time of journey = 6 hours
Therefore,
Time of travel at 55 km/h = 3 hours
Therefore, distance travelled at this speed = 55 × 3 = 165 km
This is our required solution.
Report a problem
Question for Practice Questions Level 2: Mixtures & Alligations - 2
Try yourself:Three pots have the same volume. The ratio of milk and water in the first, second and third pots is 3 : 2, 7 : 3 and 11 : 4, respectively. What is the ratio of milk and water in the new mixture if liquids of the three pots are mixed?
Explanation
Required ratio  = 61 : 29
= 61 : 29
Report a problem
Question for Practice Questions Level 2: Mixtures & Alligations - 2
Try yourself:Gold is 19 times and copper is 9 times as heavy as water. In what ratio should these metals be mixed so that the mixture is 15 times as heavy as water?
Explanation
Applying the rule of alligation,

Gold : Copper = 6 : 4 = 3 : 2
Report a problem
Question for Practice Questions Level 2: Mixtures & Alligations - 2
Try yourself:A certain alloy contains 5 parts of A and 3 parts of B by weight. Another alloy contains 6 parts of A and 7 parts of B by weight. How much amount of A (in lbs) in its pure state must be melted along with 20 lbs of the first alloy and 65 lbs of the second so as to produce a new alloy containing 40% of B by weight?
Explanation
20 lbs of the first alloy contains 20 × 5/8 of A (in lbs) and 20 × 3/8 of B (in lbs).
65 lbs of the second alloy contains 65 × 6/13 of A (in lbs) and 65 × 7/13 of B (in lbs).
Suppose X lbs of pure A is required.
⇒ (X + 65 + 20) × 
⇒ X = 21.25 lbs
Report a problem
Question for Practice Questions Level 2: Mixtures & Alligations - 2
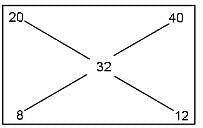
Try yourself:Kalicharan gets some coins made of an alloy of gold and silver. The alloy with a weight of 100 gm contains 20% of gold. What weight of another gold-silver alloy containing 60% of silver must be alloyed with the first piece of alloy in order to obtain a new alloy with 32% of gold?
Explanation
Gold in the first alloy = 20%
Gold in the second alloy = 40%
By alligation:

Ratio of the two alloys = 2 : 3
Quantity of the second alloy = 100 × 3/2 = 150 gm
Report a problem
Question for Practice Questions Level 2: Mixtures & Alligations - 2
Try yourself:A shopkeeper had 10 kg of rice, bought at the rate of Rs. 40 per kg and bought another 30 kg of rice at the rate of 20 per kg and mixed the two. At what price per kg should he sell the mixture to get 15% profit on the cost price?
Explanation
Cost price of the mixture = (10 × 40 + 30 × 20) = 1000
Selling price of the mixture = Cost price + (Cost price × 15%)
Selling price of the mixture = 1000 + 
Per kg selling price =  = = 28.75
= = 28.75
Report a problem
Question for Practice Questions Level 2: Mixtures & Alligations - 2
Try yourself:Two equal containers are filled with a mixture of water and alcohol. One of them contains three times as much alcohol as the other. The mixtures in the two containers are then mixed and it is found that the ratio of water to alcohol is 3 : 2. Find the ratio of water to alcohol in each of the original containers.
Explanation
Let, the volume of each container = V
Now according to the question:
In container 1 W : A = V - 3x : 3x
In container 2 W : A = V - x : x
Now

V - 2x = 3x
V = 5x
So, In container 1 W : A = 2x : 3x = 2 : 3
In container 2 W : A = 4x : x = 4 : 1
Report a problem
Question for Practice Questions Level 2: Mixtures & Alligations - 2
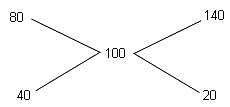
Try yourself:A merchant buys a brand of tea at Rs. 80 per kg and mixes it with another brand bought at Rs. 140 per kg. He makes a profit of 25% on selling the mixture at Rs. 125 per kg. What is the ratio in which the brands are mixed?
Explanation
Report a problem
Question for Practice Questions Level 2: Mixtures & Alligations - 2
Try yourself:A vessel contains 40 litres of milk. A milkman delivers 10 litres to the first house and adds an equal quantity of water. He does the same with the second and the third houses. What is the ratio of milk to water when he has finished delivering at the third house?
Explanation
Total amount of milk = 40 litres
Amount of milk replaced by water = 10 litres
Now, ratio of milk to the total mixture = 
Water content in the mixture = 64 - 27 = 37
Hence, ratio of milk to water = 27 : 37
Report a problem
Question for Practice Questions Level 2: Mixtures & Alligations - 2
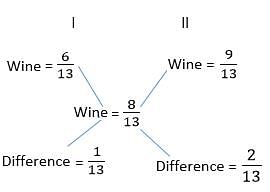
Try yourself:Cask I contains wine and water in the respective ratio 6 : 7 and cask II contains wine and water in the respective ratio 9 : 4. In what ratio must the contents of the two casks be mixed to get a mixture of wine and water in the respective ratio 8 : 5?
Explanation
Report a problem
Question for Practice Questions Level 2: Mixtures & Alligations - 2
Try yourself:A container is full of sugar syrup. 4 gallons of syrup is drawn out of the container and replaced with water. From this water-syrup mixture, 4 gallons of mixture is again withdrawn and replaced with water. The ratio of the sugar syrup to water in the container was then found to be 36 : 13. How many gallons does the container hold?
Explanation
Sugar : Water = 36 : 13
Sugar syrup in the container =  of the total volume of the container.
of the total volume of the container.
After repeating the process twice, we have

Report a problem
Question for Practice Questions Level 2: Mixtures & Alligations - 2
Try yourself:We have three solutions of milk A, B and C. Solutions A, B and C contain milk and water in the ratios of 1 : 3, 2 : 3 and 3 : 2, respectively. If we mix them in the ratio 1 : 2 : 3, respectively, then what is the ratio of milk and water in the new solution?
Explanation
Report a problem
Question for Practice Questions Level 2: Mixtures & Alligations - 2
Try yourself:Two metals X and Y are to be used for making two different alloys. If the ratio by weight of X : Y in the first alloy is 6 : 5 and that in the second is 7 : 13, then how many kilograms of X metal must be melted along with 11 kg of the first alloy and 20 kg of the second, so as to produce a new alloy containing 40% of metal Y?
Explanation
Let x kg of metal X be added.
Weight of metal X in the first alloy = 6/11 × 11 kg = 6 kg
Weight of metal X in the second alloy = 7/20 × 20 kg = 7 kg
Total weight of new alloy = (11 + 20 + x) kg
Total weight of metal X in the new alloy = (6 + 7 + x) kg.

130 + 10x = 186 + 6x
4x = 56
x = 14 kg
Report a problem
Question for Practice Questions Level 2: Mixtures & Alligations - 2
Try yourself:A solution contains a mixture of liquid A and B in the ratio of 3 : 2. When 10 litre of solution is taken out and replaced by 10 litre of liquid B, the ratio of liquids A and B in the new solution is 1 : 2. What was the volume of the initial solution?
Explanation
Report a problem
Question for Practice Questions Level 2: Mixtures & Alligations - 2
Try yourself:Two containers contain a mixture of milk and water. In one container, the ratio of milk to water is 4 : 1 and the ratio of milk to water in the other container is 1 : 3. 10 litres of mixture from the first container and 16 litres of mixture from the second container is mixed together in a third container, already containing some amount of pure milk. In the new mixture, it was found that the ratio of milk to water was 3 : 2. Find the volume of the new mixture.
Explanation
Report a problem


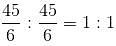
 = 61 : 29
= 61 : 29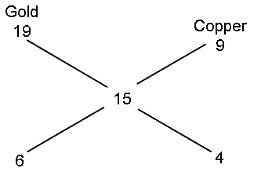
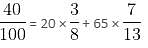
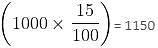
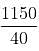 = = 28.75
= = 28.75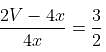
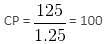
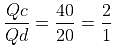
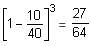
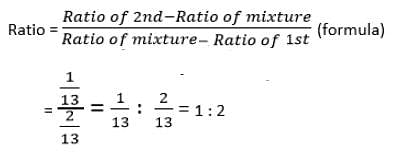
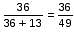 of the total volume of the container.
of the total volume of the container.
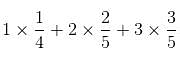 = 1/4 + 4/5 + 9/5 = (5 + 16 + 36)/20 = 57/20
= 1/4 + 4/5 + 9/5 = (5 + 16 + 36)/20 = 57/20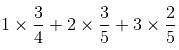 = 3/4 + 6/5 + 6/5 = (15 + 24 + 24)/20 = 63/20
= 3/4 + 6/5 + 6/5 = (15 + 24 + 24)/20 = 63/20 = 57 : 63 = 19 : 21
= 57 : 63 = 19 : 21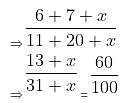
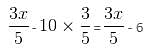
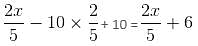
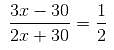
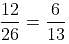
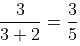

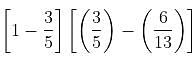 = 26 : 9
= 26 : 9
















