This EduRev document offers 20 Multiple Choice Questions (MCQs) from the topic Number System (Level - 2). These questions are of Level - 2 difficulty and will assist you in the preparation of CAT & other MBA exams. You can practice/attempt these CAT Multiple Choice Questions (MCQs) and check the explanations for a better understanding of the topic.
Question for Practice Questions Level 2: Number System - 2
Try yourself:Find the last digit of the following sum.
1! + 2! + 3! + 4! + ... + 100!
Explanation
1! = 1 (Units digit = 1)
2! = 2 × 1 = 2 (Units digit = 2)
3! = 3 × 2 × 1 = 6 (Units digit = 6)
4! = 4 × 3 × 2 × 1 = 24 (Units digit = 4)
5! = 5 × 4 × 3 × 2 × 1 = 120 (Units digit = 0)
6! = 6 × 5 × 4 × 3 × 2 × 1 = 720 (Units digit = 0)
So, we can see that the units digit of all the factorials from 5! onwards is 0.
So, the units digit of the given sum depends upon the sum of the units digits of 1!, 2!, 3! and 4!, which is 3 (6 + 4 + 2 + 1).
Report a problem
Question for Practice Questions Level 2: Number System - 2
Try yourself:How many two-digit numbers are factors of 385?
Explanation
385 = 5 × 7 × 11
Hence, 2-digit factors are 11, 35, 55 and 77
Report a problem
Question for Practice Questions Level 2: Number System - 2
Try yourself:There are two co-primes such that one number is exactly 8 times the other. What is the sum of the two numbers?
Explanation
Co-prime means, the integers which have their HCF as 1, they don`t have any common factor other than 1.
So, the numbers must be 1 and 8.
∴ Sum = 1 + 8 = 9
Report a problem
Question for Practice Questions Level 2: Number System - 2
Try yourself:If u is an even number and v and w are odd numbers, then which of the following is not an odd number?
Explanation
Let (u, v, w) be (4, 1, 3), respectively.
Start testing from the last choice.
(5): uv + w = 4 + 3 = 7, which is odd
(4): (v + w)2 - u2 = 16 - 16 = 0,
So, we can stop here and choose (4) as the answer.
(You can independently verify that the other three choices are odd integers)
Report a problem
Question for Practice Questions Level 2: Number System - 2
Try yourself:If x and y are two co-primes, then which of the following is true?
Explanation
We cannot say anything about (1), (2) and (4).
But, if x and y are co-primes, then they do not have any common factors and hence, neither do their squares.
Report a problem
Question for Practice Questions Level 2: Number System - 2
Try yourself:If a + b = c, where a, b and c are positive single-digit integers, what is the greatest possible value of the product abc?
Explanation
For the value abc to be the largest, one of them must be equal to 9. So, the possible values for (c, b, a) consistent with the equation a + b = c, are (9, 1, 8); (9, 2, 7); (9, 3, 6); (9, 4, 5); (9, 5, 4); (9, 6, 3); (9, 7, 2) and (9, 8, 1). Their products are 72, 126, 162, 180, 180, 162, 126 and 72, respectively. Among these, 180 is the largest.
Report a problem
Question for Practice Questions Level 2: Number System - 2
Try yourself:Which of the following must be true for three positive consecutive integers?
I. Their product is always divisible by 6.
II. Their sum is always divisible by 3.
III. Their product is always divisible by 4.
Explanation
Let us consider two sets of positive consecutive integers starting with an odd number and an even number, respectively i.e. (1, 2, 3) and (2, 3, 4).
I is true in both cases.
II is true in both cases.
III is not true in the first case.
So, (4) is the answer.
Report a problem
Question for Practice Questions Level 2: Number System - 2
Try yourself:Find the last two digits of 2563 × 6325.
Explanation
The last two digits of 2563 are always 25.
Last two digits of 6325 = (34 × 6)3 = (81)6 × 3 = 481 × 3 = 243 (An even number digit) 3
(Tens digit of any power of a number, whose units digit is odd and tens digit is even, is always even.)
Thus, the last two digits of 2563 × 6325 will be given by 25 × 43 (where a is even).
So, 75 is the required answer.
Report a problem
Question for Practice Questions Level 2: Number System - 2
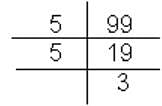
Try yourself:Find the smallest value of x such that x! ends with exactly 23 zeros.
Explanation
If we check, 99! ends with 22 zeros.

19 + 3 = 22
Likewise, 100! ends with 24 zeros.

20 + 4 = 24
So, none of the numbers ends with 23 zeros.
Report a problem
Question for Practice Questions Level 2: Number System - 2
Try yourself:How many two-digit numbers have exactly five factors?
Explanation
The number which has five factors should be of the form a4.
Such two-digit numbers are 24 and 34.
Report a problem
Question for Practice Questions Level 2: Number System - 2
Try yourself:If N = 15 × 30 × 45 × 60 × … × 1500, what will be the number of zeros at the end of N?
Explanation
N = (15 × 1)(15 × 2)...(15 × 100)= 15100 (1.2.3.4…100)
= 15100 × 100!
= (3100 × 5100)(524 × 297 × K)
So, N will have total 97 zeros.
Report a problem
Question for Practice Questions Level 2: Number System - 2
Try yourself:A number when divided by a divisor left a remainder of 23. When twice the number was divided by the same divisor, the remainder was 11. Find the divisor.
Explanation
Let the number being divided be a.
Let the divisor be y and the quotient be z. Since a = zy + 23 (given), 2a = 2zy + 46.
Since the remainder is only 11 when 2a is divided by y, the remainder is also divisible by y and its remainder will be 11. Therefore, 46 = y + 11. On solving, we get y = 35, which is the divisor.
Report a problem
Question for Practice Questions Level 2: Number System - 2
Try yourself:The arithmetic mean of two numbers is smaller by 24 than the larger of the two numbers and the GM of the same numbers exceeds by 12 the smaller of the numbers. Find the numbers.
Explanation
If a and b are two numbers, then their Arithmetic mean is given by (a + b)/2 while their geometric mean is given by (ab)0.5.
Using the options to meet the conditions we can see that for the numbers in the first option (6 and 54) the AM being 30, is 24 less than the larger number while the GM being 18, is 12 more than the smaller number.
Option (a) is correct.
Report a problem
Question for Practice Questions Level 2: Number System - 2
Try yourself:Given x and n are integers, (15n3 + 6n2 + 5n + x)/n is not an integer for what condition?
Explanation
Since 15n3, 6n2 and 5n would all be divisible by n, the condition for the expression to not be divisible by n would be if x is not divisible by n. Option (c) is correct.
Report a problem
Question for Practice Questions Level 2: Number System - 2
Try yourself:If a number is multiplied by 22 and the same number is added to it, then we get a number that is half the square of that number. Find the number
Explanation
If the number is n, we will get that 22n + n = 23n is half the square of the number n.
Thus, we have
n2 = 46 n → n = 46
Report a problem
Question for Practice Questions Level 2: Number System - 2
Try yourself:The sum of two numbers is 20 and their geometric mean is 20% lower than their arithmetic mean. Find the ratio of the numbers.
Explanation
If we assume the numbers as 16 and 4 based on 4:1 (in option a), the AM would be 10 and the GM = 8 a difference of 20% as stipulated in the question. Option (a) is correct.
Report a problem
Question for Practice Questions Level 2: Number System - 2
Try yourself:The highest power on 990 that will exactly divide 1090! is
Explanation
990 = 11 × 32 × 2 × 5. The highest power of 990 which would divide 1090! would be the power of 11 available in 1090.
This is given by [1090/11] + [1090/121] = 99 + 9 = 108
Report a problem
Question for Practice Questions Level 2: Number System - 2
Try yourself:If 146! is divisible by 6n, then find the maximum value of n.
Explanation
For finding the highest power of 6 that divides 146!, we need to get the number of 3’s that would divide 146!.
The same can be got by: [146/3] + [48/3] + [16/3] + [5/3] = 70.
Report a problem
Question for Practice Questions Level 2: Number System - 2
Try yourself:The expression 333555 + 555333 is divisible by
Explanation
Both 333555 and 555333 are divisible by 3,37 and 111.
Further, the sum of the two would be an even number and hence divisible by 2.
Thus, all the four options divide the given number.
Report a problem
Question for Practice Questions Level 2: Number System - 2
Try yourself:The units digit of a two-digit number is greater than its tens digit by 2, and the product of that number by the sum of its digits is 144. Find the number.
Explanation
The given conditions are satisfied for the number 24.
Report a problem