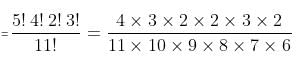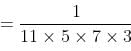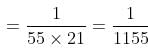This EduRev document offers 10 Multiple Choice Questions (MCQs) from the topic Probability (Level - 2). These questions are of Level - 2 difficulty and will assist you in the preparation of CAT & other MBA exams. You can practice/attempt these CAT Multiple Choice Questions (MCQs) and check the explanations for a better understanding of the topic.
Question for Practice Questions Level 2: Probability - 1
Try yourself:There are 5 Engineering books, 4 Mathematics books and 2 Physics books on a shelf, placed randomly. Find the probability that all the books of each kind are placed together.
Explanation
Report a problem
Question for Practice Questions Level 2: Probability - 1
Try yourself:Tickets numbered from 1 to 25 are mixed up together and a ticket is drawn at random. What is the probability that the drawn ticket contains a odd number?
Explanation
Total odd numbers between 1 to 25 = 13
Hence, probability = 13/25
Report a problem
Question for Practice Questions Level 2: Probability - 1
Try yourself:A pair of dice is thrown. Find the probability of the numbers appearing whose sum is greater than or equal to 10.
Explanation
Total number of possible cases = 36
Favourable events = (4, 6) (5, 5) (6, 4) (5, 6) (6, 5) (6, 6) = 6
Required probability = 6/36 = 1/6
Report a problem
Question for Practice Questions Level 2: Probability - 1
Try yourself:One hundred identical coins, each with probability 'p' of showing up heads, are tossed once. If the probability of heads showing on 50 coins is equal to that of heads showing on 51 coins, find the value of p.
Explanation
Suppose, X denotes the number of coins showing heads up.
Then, X is a binomial variate with n = 100 and probability of success p.
We have, P (X = 51) = P (X = 50)
100C51 (p)51 (1 - p)49 = 100C50 (p)50 (1 - p)50

50p = 51 - 51p
101p = 51
p = 51/101
Report a problem
Question for Practice Questions Level 2: Probability - 1
Try yourself:In a box, there are 5 Nestle and 18 Dairy Milk chocolates. Mohan picks up a chocolate without looking at it. What is the probability that it will be a Nestle chocolate?
Explanation
Number of Nestle chocolates = 5
Number of Dairy Milk chocolates = 18
Total number of chocolates = 18 + 5 = 23
Probability that a picked up chocolate is Nestle = 5/23
Report a problem
Question for Practice Questions Level 2: Probability - 1
Try yourself:A trader saves 10% in buying goods from a manufacturer in place of that from a wholesaler and sells at 10% above the wholesale price. What percent does he gain overall?
Explanation
Suppose wholesale price = Rs. 100
Since the trader buys at Rs. 90 and sells at Rs. 110,
Therefore, the required profit percentage = [(110 - 90)/90] × 100 = 22.22%
Report a problem
Question for Practice Questions Level 2: Probability - 1
Try yourself:Five boys and 3 girls are to be seated on chairs arranged in a row. If the arrangement is made at random, find the probability that no two girls will be seated next to each other.
Explanation
Five boys and three girls can be seated on 8 chairs in 8! different ways.
_ B _ B _ B _ B _ B _
As shown above, 5 boys can be seated at 5 places in 5! ways. After this, 3 girls can be seated in the remaining 6 places in 6P3 ways.
Favourable outcomes = 5! × 6P3
Probability = (5!/3!) × (6!/8!) = 5/14
Report a problem
Question for Practice Questions Level 2: Probability - 1
Try yourself:In a class, 30% of the students passed in English, 20% of the students passed in Hindi and 10% passed in both. If a student is selected at random, what is the probability that he passed in English or Hindi?
Explanation
P(E) = 30/100 = 3/10, P(H) = 20/100 = 1/5, P(E ∩ H) = 10/100 = 1/10.
P(English or Hindi) = P(E ∪ H) = P(E) + P(H) – P(E ∩ H) = 4/10 = 2/5.
Report a problem
Question for Practice Questions Level 2: Probability - 1
Try yourself:A sample space consists of numbers from 0 to 20. What is the probability that an element of the sample space is an even number, excluding numbers 0 and 20?
Explanation
Sample space is 21.
Even numbers between 0 and 20 are {2, 4, 6, 8, 10, 12, 14, 16, 18}
Number of favourable cases = 9
Hence, the probability is 9/21 = 3/7.
Report a problem
Question for Practice Questions Level 2: Probability - 1
Try yourself:Two dices are thrown simultaneously. What is the probability of getting two numbers whose sum is odd?
Explanation
S = sample space. n(S) = 36.
E = event of getting two numbers whose sum is odd = {(1, 2), (1, 4), (1, 6), (2, 1), (2, 3), (2, 5), (3, 2), (3, 4), (3, 6), (4, 1), (4, 3), (4, 5), (5, 2), (5, 4), (5, 6), (6, 1), (6, 3), (6, 5)}.
n(E) = 18.
P(E) = n(E)/n(S) = 18/36 = 1/2.
Report a problem