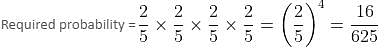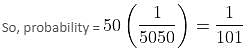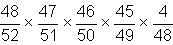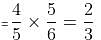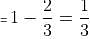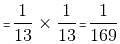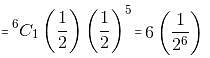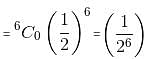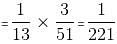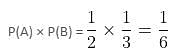This EduRev document offers 20 Multiple Choice Questions (MCQs) from the topic Probability (Level - 2). These questions are of Level - 2 difficulty and will assist you in the preparation of CAT & other MBA exams. You can practice/attempt these CAT Multiple Choice Questions (MCQs) and check the explanations for a better understanding of the topic.
Question for Practice Questions Level 2: Probability - 2
Try yourself:If four whole numbers taken at random are multiplied together, find the probability that the last digit in the product is 1, 3, 7, or 9.
Explanation
The last digit in the product can be one of the required digits, if and only if, the last digit of each of the numbers is one of the numbers 1, 3, 7 or 9.
Probability of choosing each of the four numbers is 4/10.
As the last digit of required numbers can be chosen in four different ways and total number of ways of choosing a digit at units place is 10,

Report a problem
Question for Practice Questions Level 2: Probability - 2
Try yourself:The numbers 1, 2, 3, …., 100 are written on 100 cards with one number on each card. The cards are placed in a hat and one card is selected. The sizes and shapes of the cards are such that the probability of selecting the card labelled with the number 'n' is equal to 'n' times the probability of selecting the card labelled 1. What is the probability that the card labelled 50 is selected?
Explanation
Let 'x' be the probability, that card labelled '1' is selected.
Probability that card labelled '2' is selected = 2x
Probability that card labelled '3' is selected = 3x and so on
Now, x + 2x + 3x + … + 100x = 1, which means x = 1/5050

Report a problem
Question for Practice Questions Level 2: Probability - 2
Try yourself:Cards are drawn one by one from a deck of 52 cards without replacement. What is the probability that four cards are drawn before the first ace (fifth card) is drawn?
Explanation
Required probability = P (drawing a non-ace each of the first four times and drawing an ace the fifth time) =

Report a problem
Question for Practice Questions Level 2: Probability - 2
Try yourself:Find the probability that a leap year selected at random contains either 53 Sundays or 53 Mondays.
Explanation
A leap year has 366 days, or 52 weeks + 2 days. This means that 52 Sundays will be there, but for the 53rd, we have to evaluate the possibility of the two extra or odd days to fall on Sunday or Monday.
The possible outcomes for two odd days can be (Mon, Tue); (Tue, Wed); (Wed, Thu); (Thu, Fri); (Fri, Sat); (Sat, Sun) and (Sun, Mon).
Number of favourable cases = 3
Required probability = 3/7
Report a problem
Question for Practice Questions Level 2: Probability - 2
Try yourself:A candidate is to be selected for an interview for two posts. The number of candidates for the first post is 5 and that for the second post is 6. Find the probability of getting at least one job.
Explanation
Probability that the candidate does not get an offer from the first interview is 4/5.
Probability that the candidate does not get an offer from the second interview is 5/6.
Total probability of not getting an offer

Hence, probability of getting at least one job 
Report a problem
Question for Practice Questions Level 2: Probability - 2
Try yourself:Two cards are drawn in succession from a pack of 52 cards. The first card should be a Queen and the second should be a King. What is the probability of doing so if the first card is replaced?
Explanation
Probability of drawing a Queen = 4/52 = 1/13
Since the first card is replaced, the pack will again have 52 cards. So, the probability of drawing a King = 4/52 = 1/13
Both the events are independent, hence the probability of drawing both cards in succession

Report a problem
Question for Practice Questions Level 2: Probability - 2
Try yourself:Six unbiased coins are tossed simultaneously. Find the probability that at least two heads occur.
Explanation
Report a problem
Question for Practice Questions Level 2: Probability - 2
Try yourself:Two numbers a and b are chosen at random from the set of first 30 natural numbers. The probability that a2 - b2 is divisible by 3 is
Explanation
The total number of ways of choosing two numbers out of 1, 2, 3 ........, 30 is
30C2 = 435
⇒ Exhaustive number of cases = 435
Since a2 - b2 is divisible by 3 if either a and b both are divisible by 3 or none of a and b is divisible by 3, so the favourable number of cases = 10C2 + 20C2 = 235
Hence, the required probability = 235/435 = 47/87
Report a problem
Question for Practice Questions Level 2: Probability - 2
Try yourself:A bag contains 5 square boxes and 7 cylindrical boxes. Two boxes are drawn at random. Find the probability that they are the same shape.
Explanation
S = sample space. n(s) = No. of ways of drawing two boxes out of (5 + 7) boxes = 12C2 = (12 × 11)/(2 × 1) = 66.
E = Event of getting both boxes of the same shape.
n(E) = No. of ways of drawing (2 boxes out of 5 or 2 boxes out of 7) = 5C2 + 7C2 = (5 × 4)/(2 × 1) + (7 × 6)/(2 × 1) = 31.
P(E) = n(E)/n(S) = 31/66.
Report a problem
Question for Practice Questions Level 2: Probability - 2
Try yourself:Consider a pack of 52 cards. One card is drawn at random. What is the probability of the card being a heart or a seven?
Explanation
S = Sample space = 52.
There are 13 hearts including 1 seven.
There are 3 more sevens in spade, club and diamond.
E = event of getting a seven or a heart.
n(E) = 13 + 3 = 16.
P(E) = n(E)/n(S) = 16/52 = 4/13
Report a problem
Question for Practice Questions Level 2: Probability - 2
Try yourself:Two cards are drawn one by one at random without replacement from a pack of 52 cards. What is the probability that the cards drawn are queens?
Explanation
Here, the sample space is 52.
Probability that the first card is a queen = 4/52 = 1/13
Probability that the second card is a queen = 3/51
Hence, probability that the cards drawn are queens

Report a problem
Question for Practice Questions Level 2: Probability - 2
Try yourself:Two fair dice are thrown. What is the probability that the number of dots on the first dice is greater than 3 and that on the second is greater than 4?
Explanation
A: The first dice shows 4, 5 or 6 dots.
B: The seconds dice shows 5 or 6 dots.
P(A) = 3/6 = 1/2
P(B) = 2/6 = 1/3
So, the required probability is

Report a problem
Question for Practice Questions Level 2: Probability - 2
Try yourself:In a room, there are 15 men and 10 women. Three of them are selected at random. The probability that 1 woman and 2 men are selected is
Explanation
S = Sample space and E = event of choosing 1 woman and 2 men.
n(S) = Number of ways of selecting 3 people out of 25

n(E) = (10C1 × 15C2) = 1050.
Therefore, P(E) = n(E)/n(S) = 1050/2300 = 21/46
Report a problem
Question for Practice Questions Level 2: Probability - 2
Try yourself:In a box, there are 5 red, 9 green and 6 black balls. One ball is picked up randomly. What is the probability that it is neither red nor green?
Explanation
Total number of balls = 5 + 9 + 6 = 20.
E = event that the ball drawn is neither red nor green = event that the ball drawn is black = 6.
Therefore, P(E) = 6/20.
Report a problem
Question for Practice Questions Level 2: Probability - 2
Try yourself:In a simultaneous throw of a pair of dice, find the probability of getting an even number on one and a multiple of 3 on the other.
Explanation
Elementary events associated to the random experiment of throwing two dice are:
(1, 1), (1, 2), (1, 3), (1, 4), (1, 5), (1, 6), (2, 1), (2, 2), (2, 3), (2, 4), (2, 5), (2, 6), (3, 1), (3, 2), (3, 3), (3, 4), (3, 5), (3, 6), (4, 1), (4, 2), (4, 3), (4, 4),(4, 5), (4, 6), (5, 1), (5, 2), (5, 3), (5, 4), (5, 5), (5, 6), (6, 1), (6, 2), (6, 3), (6, 4), (6, 5), (6, 6)
Total no. of events = 36
Let A be the event of getting an even number on one and a multiple of 3 on the other.
A : (2, 3), (2, 6), (3, 2), (3, 4), (3, 6), (4, 3), (4, 6), (6, 2), (6, 3), (6, 4), (6, 6)
So, favourable no. of events = 11
Hence, probability = (No. of favourable events)/(Total no. of events)
Probability = 11/36
Report a problem
Question for Practice Questions Level 2: Probability - 2
Try yourself:A bag contains 4 yellow balls, 5 green balls and 3 red balls. What is the probability of drawing a red or a yellow ball?
Explanation
Total number of balls = 4 + 3 + 5 = 12
Number of balls which are either red or yellow = 3 + 4 = 7
Here, the total sample space is 12 and the event value is 7.
Hence, probability of getting a red or a yellow ball = 7/12
Report a problem
Question for Practice Questions Level 2: Probability - 2
Try yourself:There are two dice; red and green. What is the probability that on roll the red die throws up a prime number which is divisible by the number thrown up on the roll of the green die?
Explanation
There are 3 cases possible as follows:
Case 1:
The red die throws up a 2 and the green die throws up a 2 or a 1, the probability of which is (1/6)(2/6) = 2/36 = 1/18
Case 2:
The red die throws up a 3 and the green die throws up a 3 or a 1, the probability of which is (1/6)(2/6) = 2/36 = 1/18
Case 3:
The red die throws up a 5 and the green die throws up a 5 or a 1, the probability of which is (1/6)(2/6) = 2/36 = 1/18
Thus, the required probability = (1/18) + (1/18) + (1/18) = 3 × (1/18) = 1/6
Report a problem
Question for Practice Questions Level 2: Probability - 2
Try yourself:Two fair dices are thrown. Given that the sum of the dice is less than or equal to 4, find the probability that only one dice shows two.
Explanation
The possible outcomes are:
(1, 1); (1, 2); (2, 1), (2, 2); (3, 1); (1, 3).
Out of six cases, in two cases there is exactly one ‘2’
Thus, the correct answer is 2/6 = 1/3.
Report a problem
Question for Practice Questions Level 2: Probability - 2
Try yourself:There are two bags, one of them contains 5 red and 7 white balls and the other 3 red and 12 white balls, and a ball is to be drawn from one or the other of the two bags. Find the chance of drawing a red ball.
Explanation
The event can be defined as:
First bag is selected and red ball is drawn.
or second bag is selected and red ball is drawn.
1/2 X 5/12 + / X 3/15 = (5/24) + (3/30) = 37/120
Report a problem
Question for Practice Questions Level 2: Probability - 2
Try yourself:If 8 coins are tossed, what is the chance that one and only one will turn up Head?
Explanation
One head and seven tails would have eight positions where the head can come.
Thus, 8 x (1/2)8 = (1/32)
Report a problem