This EduRev document offers 10 Multiple Choice Questions (MCQs) from the topic Ratio & Proportion (Level - 2). These questions are of Level - 2 difficulty and will assist you in the preparation of CAT & other MBA exams. You can practice/attempt these CAT Multiple Choice Questions (MCQs) and check the explanations for a better understanding of the topic.
Question for Practice Questions Level 2: Ratio & Proportion - 1
Try yourself:A loaf of bread with weight 60 grams is cut into three unequal pieces. The ratio of the weights of heaviest and the lightest pieces is 5 : 1. If the middle weighted piece is 18 grams heavier than the lightest, then what is the weight of the heaviest piece?
Explanation
Assume the weight of the heaviest piece = 5x
Then, the weight of the lightest piece = x
So, the weight of medium weighted piece = x + 18
∴ (5x) + (x + 18) + (x) = 60
⇒ x = 6
So, the weight of the heaviest piece = 5 × 6 = 30 grams
Report a problem
Question for Practice Questions Level 2: Ratio & Proportion - 1
Try yourself:If A gives half of his candies to B, then B will have 30% more candies than what he had earlier. What is the ratio of candies with A and B?
Explanation
Assume A has x candies and B has y candies.
If he gives half to B, i.e x/2 then B will have 1.3y candies.
Thus,
0.3y = x/2

Report a problem
Question for Practice Questions Level 2: Ratio & Proportion - 1
Try yourself:There are six bottles of same capacity that are filled with water. The quantities of water in all the bottles are in the ratio 1 : 2 : 3 : 4 : 5 : 6. The water in each of the bottles is poured into an empty jar whose capacity is half the total capacity of the six bottles. The jar is filled up completely. How many bottles were at least 70% filled with water initially?
Explanation
Let the amounts of water in the bottles be V, 2V, 3V, 4V, 5V and 6V.
So, total water poured = 21V
Let the capacity of each bottle be C.
So, capacity of six bottles = 6C
Capacity of jar = 3C
As the jar is completely filled, we have
21V = 3C
Or 7V = C
Now, 70% of 7V = 4.9V
Thus, there are two bottles which were at least 70% filled with water.
Hence, answer option 3 is correct.
Report a problem
Question for Practice Questions Level 2: Ratio & Proportion - 1
Try yourself:Set A contains 10 consecutive numbers starting from x and set B contains 8 consecutive even numbers starting from y. The ratio of the average of set A elements to that of set B elements is 9 : 14. What is the ratio of x to y?
Explanation
Average of set A elements = x + 4.5
Average of set B elements = y + 7
So,  = 9/14
= 9/14
⇒ 14x + 63 = 9y + 63
⇒ x/y = 9/14
Report a problem
Question for Practice Questions Level 2: Ratio & Proportion - 1
Try yourself:A is working and B is the sleeping partner in a business. A invests Rs. 12,000 and B invests Rs. 20,000. A receives 10% of the profit for managing. The rest is divided in the ratio of their capitals. Out of a total profit of Rs. 9600, what will be the amount received by A?
Explanation
A gets 10% of the profit for managing the business = 10% of 9600 = Rs. 960
Profit remaining = 9600 - 960 = Rs. 8640
Ratio in which they will share the remaining profit = 12 : 20 = 3 : 5
A's share = 960 + (3/8) 8640 = Rs. 4200
Report a problem
Question for Practice Questions Level 2: Ratio & Proportion - 1
Try yourself:The sum of three numbers is 98. The ratio of the first two numbers is 2 : 3 and that of the last two numbers is 5 : 8. Find the 2nd number.
Explanation
Let the numbers be x, y and z.
x + y + z = 98
Also, x : y = 2 : 3 and y : z = 5 : 8
Therefore, x : y : z = 10 : 15 : 24
Let x = 10k, y = 15k and z = 24k
Then, 10k + 15k + 24k = 98
⇒ k = 2
The numbers are 20, 30 and 48.
Hence, second number is 30.
Report a problem
Question for Practice Questions Level 2: Ratio & Proportion - 1
Try yourself:If (a + b) : (b + c) : (c + a) = 6 : 7 : 8 and (a + b + c) = 14, then the value of c is
Explanation
Let (a + b) = 6k, (b + c) = 7k and (c + a) = 8k.
Then, 2 (a + b + c) = 21k
2 × 14 = 21k
k = 28/21 = 4/3
(a + b) = (6 × 4/3) = 8
c = (a + b + c) - (a + b) = (14 - 8) = 6
Report a problem
Question for Practice Questions Level 2: Ratio & Proportion - 1
Try yourself:A purse contains notes of Re. 1, Rs. 10 and Rs. 20 only. The number of notes of Re. 1 is seven times the number of notes of Rs. 10 and the number of notes of Rs. 20 is 4 times the number of notes of Rs. 10. How much money is there in the purse if there are total twelve notes of Rs. 20?
Explanation
Number of notes of Rs. 20 = 12
Number of notes of Rs. 10 = 12/4 = 3
Number of notes of Re. 1 = 7 × 3 = 21
Total amount = 12 × 20 + 3 × 10 + 1 × 21 = 240 + 30 + 21 = Rs. 291
Report a problem
Question for Practice Questions Level 2: Ratio & Proportion - 1
Try yourself:A 60 year old father in his will divides his money among his three sons in the ratio of their ages. The first (eldest) son is 8 years older than the third son. The second son is 4 years younger to the first son. The third son's age is 1/3rd of his father's age. If the father had Rs. 12,00,000, the share of second son is:
Explanation
The age of 3rd son = 1/3 × 60 = 20 yrs
Age of 1st son = 20 + 8 = 28 yrs
Age of 2nd son = 28 - 4 = 24 years
Ratio of their ages = 28 : 24 : 20 = 7 : 6 : 5
As per question, 7x + 6x + 5x = 12,00,000, i.e., 18x = 12,00,000
So, x = 66,666.66
Share of 2nd son = 6x = 6 × 66,666.66 = Rs. 4,00,000
Report a problem
Question for Practice Questions Level 2: Ratio & Proportion - 1
Try yourself:Brian and Sam are two brothers who work at a multinational company in the New York City. The ratio of monthly incomes of Brian and Sam is 3 : 4 and the ratio of their monthly savings is 2 : 3, respectively. It is known that Brian spends two-thirds of his income each month. Find the respective ratio of their monthly expenditures.
Explanation
It is known that expenditure of Brian is 2rd/3 of his income.
Let Brian`s monthly income be $36.
Then, his expenditure will be $24.
Total savings of Brian = $12
Ratio of savings of Brian to that of Sam is given as 2 : 3.
Hence, savings of Sam = $18
Now, ratio of incomes = Brian : Sam = 3 : 4
As Brian`s income = $36, then income of Sam will be $48.
So, ratio of expenditure of Brian to that of Sam = 24 : 30 or 4 : 5
Report a problem


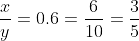
 = 9/14
= 9/14















