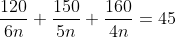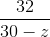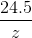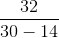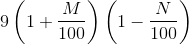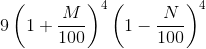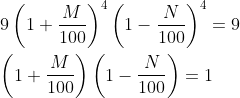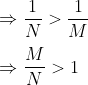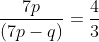This EduRev document offers 20 Multiple Choice Questions (MCQs) from the topic Ratio & Proportion (Level - 2). These questions are of Level - 2 difficulty and will assist you in the preparation of CAT & other MBA exams. You can practice/attempt these CAT Multiple Choice Questions (MCQs) and check the explanations for a better understanding of the topic.
Question for Practice Questions Level 2: Ratio & Proportion - 2
Try yourself:On her birthday, Ritu distributes 124 chocolates in her class. She gives 4 chocolates to each girl and 3 chocolates to each boy. If she had given 2 chocolates to each boy and girl, she would have saved 52 chocolates. The ratio of number of girls to boys in Ritu's class is:
Explanation
Let x be the number of boys and y be the number of girls in Ritu's class.
Based on the chocolate distribution,
3x + 4y = 124
Had she given 2 chocolates to each boy and girl:
2x + 2y = 124 - 52 = 72
Solving both equations, we get
x = 20 and y = 16
Ratio of girls to boys = y/x = 16/20 = 4 : 5
Report a problem
Question for Practice Questions Level 2: Ratio & Proportion - 2
Try yourself:Glass A is filled with 2/3rd of wine and the remaining portion is filled with water. Similarly, glass B of same size is filled with 4/7th of wine and remaining with water. The contents of the two glasses are poured in a tumbler and mixed. The ratio of water to wine in the tumbler is:
Explanation
Glasses A and B have same volume, let it be 1 L.
Glass A has 2/3 L of wine and 1/3 L of water.
Glass B has 4/7 L of wine and 3/7 L of water.
Total water in the mixture = (1/3 + 3/7) L = 16/21 L
Total wine in the mixture = (2/3 + 4/7) L = 26/21 L
Ratio = (16/21)/(26/21) = 16/26 = 8/13
Report a problem
Question for Practice Questions Level 2: Ratio & Proportion - 2
Try yourself:Of all the students in a certain dormitory, half are first-year students and the rest are second-year students. If 4/5 of the first-year students have not declared a major and the fraction of second-year students who have declared a major is 3 times the fraction of the first-year students who have declared a major, then what fraction of all the students in the dormitory are second-year students who have not declared a major?
Explanation
Suppose total number of students in a certain dormitory = y
Then, total number of first-year students = y/2
Total number of first-year students who have not declared a major = (2/5)y
So, fraction of first-year students who have declared a major = (1/10)y
Total number of fraction of second-year students who have declared a major = (3/10)y
Total number of fraction of second-year students who have not declared a major = (1/5)y
Then, required fraction = (1/5)
Report a problem
Question for Practice Questions Level 2: Ratio & Proportion - 2
Try yourself:Directions: In a paper of CAT there are 3 sections, each contains 25 questions and each question carries 4 marks. Wrong answer carries 1 mark negative. There is no negative or positive marking for not attempted question. A student attempted the questions from section A, B and C in the ratio 6 : 5 : 4. The number of correct answers are in the ratio 4 : 3 : 2, respectively. The student got 96 marks in section A.
Q. How many marks will the student get in section C?
Explanation
Since he scored 96 marks in section A, he must have attempted 24 questions in that section and all should have been right.
So,
Number of questions attempted in section A = 24
Number of questions attempted in section B = 20
Number of questions attempted in section C = 16
And,
Number of correct attempted questions in section A = 24
Number of correct attempted questions in section B = 18
Number of correct attempted questions in section C = 12
Thus, in section C, he will get:
12 × 4 - 4 = 44 marks
Report a problem
Question for Practice Questions Level 2: Ratio & Proportion - 2
Try yourself:The cost of a diamond varies directly as the square of its weight. Once, this diamond broke into four pieces with weights in the ratio 1 : 2 : 3 : 4. When the pieces were sold, the merchant got Rs. 70,000 less. Find the original price of the diamond.
Explanation
Cost ∝ Weight2
Let original weight = 10x
Then, original cost = 100x2k (where k is proportionality constant)
After breakage weight = 1x + 2x + 3x + 4x
After breakage cost = kx2(1 + 4 + 9 + 16) = 30x2k
Now, (100 - 30)x2k = 70,000
Or, 70x2k = 70,000
Or, x2k = 1,000
Hence, original cost = 100x2k
= 100 × 1,000 = Rs. 1,00,000
Report a problem
Question for Practice Questions Level 2: Ratio & Proportion - 2
Try yourself:A sum of Rs. 735 was divided among A, B and C. If each of them had received Rs. 25 less, then their shares would have been in the ratio 1 : 3 : 2. What is the money received by C?
Explanation
Suppose after the reduction of Rs. 25, the shares of A, B and C are x, 3x and 2x, respectively.
Total money = 6x (after reduction)
Initially, share (A) + share (B) + share (C) = 735 … (1)
After reduction,
share (A) - 25 + share (B) - 25 + share (C) - 25 = 6x
⇒ share (A) + share (B) + share (C) - 75 = 6x ... (2)
From (1) and (2), we get
⇒ 735 - 75 = 6x
⇒ x = 660/6 = 110
Now, after deduction, C has, 2x = 2 × 110 = Rs. 220.
Before deduction, C had, 220 + 25 = Rs. 245
Report a problem
Question for Practice Questions Level 2: Ratio & Proportion - 2
Try yourself:$430 is divided among 45 persons consisting of men, women and children. The sum of shares of men, women and children is in the ratio 12 : 15 : 16, but the individual shares of a man, a woman and a child are in the ratio 6 : 5 : 4. Find the share of each man, woman and child, respectively.
Explanation
Share of men = (12/43) × 430 = $ 120
Share of women = (15/43) × 430 = $ 150
Share of children = (16/43) × 430 = $ 160
Ratio of individual share = 6 : 5 : 4
So, individual shares be 6n, 5n and 4n, respectively.
Number of members = 45
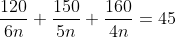
n = 2
So, individual shares are $12, $10 and $8, respectively.
Report a problem
Question for Practice Questions Level 2: Ratio & Proportion - 2
Try yourself:P and Q are two different mouth fresheners, prepared by mixing Supari and Saunf in the ratios 9 : 4 and 9 : 17, respectively. If equal quantities of the P and Q mouth fresheners are mixed to form a third kind of mouth freshener R, find the ratio of Saunf and Supari in R.
Explanation
In P, quantity of Supari = 9/13
And quantity of Saunf = 4/13
In Q, quantity of Supari = 9/26
And quantity of Saunf = 17/26
When we add these two mouth fresheners:
Total quantity of Supari = 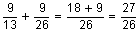
Total quantity of Saunf = 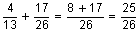
So, ratio of Saunf and Supari in R = 25 : 27
Report a problem
Question for Practice Questions Level 2: Ratio & Proportion - 2
Try yourself:Eight bananas and six apples cost a certain amount. If the cost of a banana increases by 10% and the cost of an apple decreases by 10%, then eight bananas and six apples will cost the same amount. What is the ratio of the cost of a banana to that of an apple?
Explanation
Let B be the cost of a banana and A be the cost of an apple.
Let x be the total cost of 8 bananas and 6 apples.
According to the question,
8B + 6A = x
8.8B + 5.4A = x
⇒ 0.8B = 0.6A
B/A = 3/4
Report a problem
Question for Practice Questions Level 2: Ratio & Proportion - 2
Try yourself:The number of goals scored by a team in a football match varies directly as the square of the number of international level players in the team. If the difference in goals scored when four and six international players participate is five goals, then how many goals will be scored when eight international level players participate?
Explanation
Let G be the number of goals scored and p be the number of international players.
G α p2
∴ G = kp2
When 4 players play, G1 = k × 42 = 16k
When 6 players play, G2 = k × 62 = 36k
G2 - G1 = 5 goals
∴ 5 = k (36 - 16) or k = ¼
When 8 players play,
G = (1/4) × 82 = 16
Report a problem
Question for Practice Questions Level 2: Ratio & Proportion - 2
Try yourself:Jagan and Rex had a total of 30 cars in their showrooms. Both sold their cars at different prices, but earned the same amount of money. If Jagan had sold his cars at Rex's price, he would have earned Rs. 32 lakh. If Rex had sold his cars at Jagan's price, he would have earned Rs. 24.5 lakh. At what price did Rex sell each of his cars?
Explanation
Total number of cars = 30
Let the number of cars sold by Rex be z.
Then, number of cars sold by Jagan = 30 - z
Let the price of each car sold by Jagan be Rs. y.
Let the price of each car sold by Rex be Rs. x.
According to the question:
xz = (30 - z)y --- (1)
And x(30 - z) = 32 lakh --- (2)
zy = 24.5 lakh --- (3)
From (2), x = 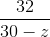 lakh
lakh
From (3), y = 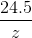 lakh
lakh
Putting the values of x and y in (1), we get
32z2 = 24.5(30 - z)2
⇒ 32z2 = 24.5(900 + z2 - 60z)
⇒ 7.5z2 = 22,050 - 1470z
⇒ z2 + 196z - 2940 = 0
⇒ z = 14, z = -210
Since number of cars sold cannot be negative, z = 14.
⇒ Number of cars sold by Rex = 14
Price of each car sold by Rex = 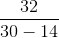 = Rs. 2 lakh
= Rs. 2 lakh
Report a problem
Question for Practice Questions Level 2: Ratio & Proportion - 2
Try yourself:The force of attraction between two bodies of mass m1 and m2 varies directly as the product of their masses and inversely as the square of the distance between them. If the masses of the bodies and the distance between them are doubled, then the force of attraction will
Explanation
Report a problem
Question for Practice Questions Level 2: Ratio & Proportion - 2
Try yourself:The Rice Tent Company sells tents in two different sizes, large and small. Last year, the company sold 200 tents, out of which one-quarter were large. The sales of the large tents produced one-third of the company`s income. What was the ratio of the price of a large tent to the price of a small tent last year?
Explanation
Now, The Rice Tent Company sold 200 tents, out of which one-quarter were large.
So, they sold 50 large tents and 150 small tents last year.
Let L be the price of a large tent and S be the price of a small tent.
Then, their income from large tents was 50L and from small tents was 150S.
Their total income last year was 50L + 150S.
From the given information:
50L = 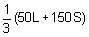
150L = 50L + 150S
100L = 150S
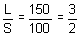
Therefore, the ratio of the price of a large tent to the price of a small tent is 3 : 2.
Report a problem
Question for Practice Questions Level 2: Ratio & Proportion - 2
Try yourself:A pet merchant started his business at the end of 2008 by buying nine score pets of different kinds. Every year he added M% of the pets at the beginning and sold N% of the pets at the end, where both M and N are more than zero. The merchant had nine score pets at the end of the year 2012, after making the sales for that year. Which of the following can be the possible value of M : N?
Explanation
Report a problem
Question for Practice Questions Level 2: Ratio & Proportion - 2
Try yourself:Robin and Robert have some money in the ratio of 4 : 3. Robin gives Rs.p to Robert. Now, they have equal amounts of money. But Robert spends Rs.q out of the total money he has. Now again, the ratio is 4 : 3. Find the ratio p : q.
Explanation
Let the amount with Robin initially = 4m
Let the amount with Robert initially = 3m
Now, amount with Robin after he gives Rs.p to Robert = 4m - p
Amount with Robert after the above said transaction = 3m + p
Now, according to question, 4m - p = 3m + p
Or, m = 2p
Now, money with Robin = 4m - p = 4 × 2p - p = 7p
Money with Robert = 3m + p = 3 × 2p + p = 7p
Now, money left with Robert after he spends Rs.q = 7p - q
Now, according to question,
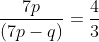
Or, 21p = 28p - 4q
Or, 4q = 7p
Or,

Hence, answer option c is correct.
Report a problem
Question for Practice Questions Level 2: Ratio & Proportion - 2
Try yourself:In an examination, the number of students who passed and those who failed were in the ratio 5 : 2. Had 25 more appeared and 5 less passed, the ratio of passed to failed would have been 3 : 2. Find the total number of students who appeared in the examination.
Explanation
Ratio of students who passed to those who failed = 5 : 2
Let the number of students who passed be 5x and those who failed be 2x.
Total number of students = 5x + 2x = 7x
When 25 more students appeared, then total students = 7x + 25
When students increased, 5 less passed = (5x - 5)
Now, number of students who passed = 5x - 5
Number of students who failed = (7x + 25) - (5x - 5) = 7x + 25 - 5x + 5 = 2x + 30
New ratio of passed to failed = 3 : 2
According to the question,
 =
= 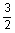
⇒ 2(5x - 5) = 3(2x + 30)
⇒ 10x - 10 = 6x + 90
⇒ 10x - 6x = 90 + 10
4x = 100
x = 25
Hence, number of students who appeared = 7 × 25 = 175
Report a problem
Question for Practice Questions Level 2: Ratio & Proportion - 2
Try yourself:If the work done by p men in (p + 2) days is to the work done by (p + 4) men in (p – 1) days is in the ratio 1 : 1, then the value of p is
Explanation
By taking the value of p = 4 from Option (b), the required ratio of 1: 1 is achieved
Report a problem
Question for Practice Questions Level 2: Ratio & Proportion - 2
Try yourself:Rahim covers a distance of 48 km performed by train, bike and car in that order, the distance covered by the three ways in that order are in the ratio of 8 : 1 : 3 and charges per kilometer in that order are in the ratio of 8 : 1 : 4. If the train charges being 24 ₹ per kilometer, the total cost of the journey is
Explanation
Total distances covered under each mode = 32, 4 and 12 km respectively.
Total charges = 32 × 24 + 4 × 3 + 12 × 12 = ₹ 924.
Report a problem
Question for Practice Questions Level 2: Ratio & Proportion - 2
Try yourself:Concentrations of three type of milks X, Y and Z are 10%, 20% and 30%, respectively. They are mixed in the ratio 2 : 3 : P resulting in a 23% concentration solution. Find P.
Explanation
(20 + 60 + 30P)/(2 + 3 + P) = 23 → 80 + 30P =
115 + 23P or P = 5
Report a problem
Question for Practice Questions Level 2: Ratio & Proportion - 2
Try yourself:In a co-educational school there are 15 more girls than boys. If the number of girls is increased by 10% and the number of boys is also increased by 16%, there would be 9 more girls than boys. What is the number of students in the school?