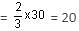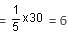This EduRev document offers 10 Multiple Choice Questions (MCQs) from the topic Set Theory (Level - 2). These questions are of Level - 2 difficulty and will assist you in the preparation of CAT & other MBA exams. You can practice/attempt these CAT Multiple Choice Questions (MCQs) and check the explanations for a better understanding of the topic.
Question for Practice Questions Level 2: Set Theory - 1
Try yourself:A = {x : x is a perfect square; x ≤ 20; x ∈ N}
B = {y : y is not a perfect square; y ≤ 20; y ∈ N}
C = A ∪ B and D = A ∩ B
Which of the following statements is/are true?
(i) (C ∪ D) ∪ D = A ∪ B
(ii) C ∩ D = Ø
(iii) C ∪ D = C
Explanation
A = {1, 4, 9, 16}
B = {2, 3, 5, 6, 7, 8, 10, 11, 12, 13, 14, 15, 17, 18, 19, 20}
C = A ∪ B and D = A ∩ B = {1, 2, 3, … 19, 20}
D = Ø
(i) (C ∪ D) ∪ D = A ∪ B
C ∪ D = C
C = C
(ii) C ∩ D = Ø
Ø = Ø
(ii) C ∪ D = C
C = C
All the statements are true.
Report a problem
Question for Practice Questions Level 2: Set Theory - 1
Try yourself:In a locality, two-thirds of the people have Cable TV, one-fifth have VCR and one-tenth have both. What is the fraction of people having either Cable TV or VCR?
Explanation
Report a problem
Question for Practice Questions Level 2: Set Theory - 1
Try yourself:In a survey of 100 persons, it was found that 39 subscribed to TV Guide, 26 subscribed to Time and 6 subscribed to Scientific American. A total of 15 subscribed to at least two of these magazines and 2 subscribed to all the three. How many persons did not subscribe to any of the three?
Explanation
A total of 15 persons subscribed to at least two of these magazines and 2 persons subscribed to all the three.
Then, 13 subscribed to exact two of these magazines.
Now, n(A) + n(B) + n(C) - [n(A ∩ B) + n(B ∩ C) + n(C ∩ A)] + n(A ∩ B ∩ C) = 39 + 26 + 6 - (13 + 2 + 2 + 2) + 2 = 54
Thus, out of 100 people surveyed, 54 subscribed to at least one of the three magazines or 46 did not subscribe to any of the three.
Report a problem
Question for Practice Questions Level 2: Set Theory - 1
Try yourself:Directions: Study the following information and answer the question.
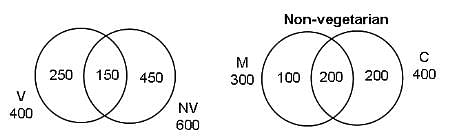
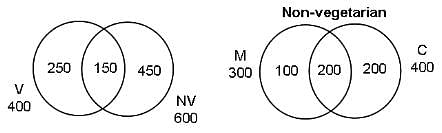
In Foodpur, where a person has to eat either vegetarian food or non-vegetarian food, there are 600 people who eat non-vegetarian food, 400 people who eat vegetarian food and 150 people who eat both. Of the people who eat non-vegetarian, there are 300 who eat mutton, 400 who eat chicken and 200 who eat both these types of meat.
Q. How many people eat vegetarian food as well as mutton?
Explanation

From the given data, number of people eating vegetarian food as well as mutton cannot be determined.
Report a problem
Question for Practice Questions Level 2: Set Theory - 1
Try yourself:Directions: Study the following information and answer the question.
In Foodpur, where a person has to eat either vegetarian food or non-vegetarian food, there are 600 people who eat non-vegetarian food, 400 people who eat vegetarian food and 150 people who eat both. Of the people who eat non-vegetarian, there are 300 who eat mutton, 400 who eat chicken and 200 who eat both these types of meat.
Q. How many people do not eat chicken or mutton?
Explanation

Number of people who eat only vegetarian food = 250
Number of people who eat non-vegetarian food = 600
Number of people who eat mutton or chicken = 100 + 200 + 200 = 500
Remaining number of non-vegetarian people who do not eat mutton or chicken = 600 - 500 = 100
So, number of people who do not eat chicken or mutton = 250 + 100 = 350
Report a problem
Question for Practice Questions Level 2: Set Theory - 1
Try yourself:At a meeting of 100 people, there were 23 Indian men and 29 Indian women. Of these Indians, 4 were dentists and 24 were either men or dentists. Assume that there were no foreign dentists. How many women dentists attended the meeting?
Explanation
It is given that 24 were either men or dentists. We know that 23 were men, so the remaining 1 must be a woman dentist.
Report a problem
Question for Practice Questions Level 2: Set Theory - 1
Try yourself:If X = {4n - 3n - 1 : n ∈ N} and Y = {9(n - 1) : n ∈ N}, then X ∪ Y is equal to
Explanation
Putting the values of n = 1, 2, 3, 4, …, we get:
X = 0, 9, 54, …
Y = 0, 9, 18, 27, 36, 45, 54, ...
Hence, X U Y will be a set equal to the value of Y.
Hence, X U Y = Y
Report a problem
Question for Practice Questions Level 2: Set Theory - 1
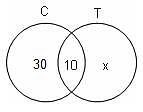
Try yourself:In a group of 65 people, 40 like cricket, 10 like both cricket and tennis. Each one likes at least one sport out of cricket and tennis.
How many people like tennis?
Explanation
C = Cricket
T = Tennis

Total number of people = 65
Let x be the number of people who like only tennis.
Number of people who like cricket = 40
Number of people both cricket and tennis = 10
From the Venn diagram,
40 - 10 + 10 + x = 65
x = 25
i.e. Number of people who like only tennis = 25
Number of people who like tennis = 25 + 10 = 35
Report a problem
Question for Practice Questions Level 2: Set Theory - 1
Try yourself:Which of the following is an empty set?
Explanation
(A × B) ∩ (B × A) will be an empty set if A and B are disjoint. This is because in (A × B) ∩ (B × A), when we use any element, it means we are finding the common elements. But A and B are disjoint sets, so we will get zero common elements. Hence, the intersection of (A × B) and (B × A) will be a null set.
Report a problem
Question for Practice Questions Level 2: Set Theory - 1
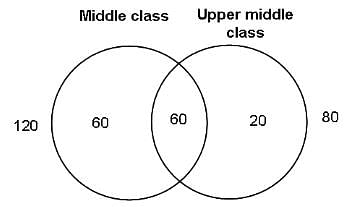
Try yourself:At a dinner where 240 men are seated, half of the men belong to the middle class, one third to the upper-middle class and one-fourth to both the classes. How many men belong to neither class?
Explanation
This problem can be solved with the help of a Venn diagram.

Number of men belonging to the middle class = 240 × (1/2) = 120
Number of men belonging to the upper class = 240 × (1/3) = 80
Number of men belonging to both the classes = 240 × (1/4) = 60
We have identified 60 + 60 + 20 = 140 men as having well-defined class.
∴ 240 – 140 = 100 men do not belong to either class.
Report a problem