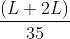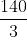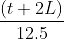This EduRev document offers 10 Multiple Choice Questions (MCQs) from the topic Speed, Time & Distance (Level - 2). These questions are of Level - 2 difficulty and will assist you in the preparation of CAT & other MBA exams. You can practice/attempt these CAT Multiple Choice Questions (MCQs) and check the explanations for a better understanding of the topic.
Question for Practice Questions Level 2: Speed, Time & Distance - 1
Try yourself:A monkey starts climbing a 15 feet tree. Each hour, he climbs 3 feet and rests for 30 minutes. During his rest, he slips back 2 feet. How many hours will the monkey take to reach the top?
Explanation
The monkey climbs 3 feet in 1 hour and drops by 2 feet in half an hour.
So, he climbs net 1 foot in (3/2) hours.
This way, he climbs 12 feet in 18 hours.
In the next hour, he will climb 3 more feet i.e. he will climb 15 feet in 19 hours and will reach the top of the tree.
Report a problem
Question for Practice Questions Level 2: Speed, Time & Distance - 1
Try yourself:A man covered a total distance of 1000 km in 16 hours, partly in a taxi at 36 km/hr and partly in a bus at 80 km/hr. The distance covered by the bus is
Explanation
Total distance = 1000 km
Total time = 16 hours
Let the time for bus travel be x hours.
Then, time for taxi travel be (16 – x) hours.
Then,
1000 = x × 80 + (16 – x)36
1000 = 80x + 576 – 36x
424 = 44x
x = 424/44 = 106/11 hours
Distance covered by bus =  = 770.9 km
= 770.9 km
Report a problem
Question for Practice Questions Level 2: Speed, Time & Distance - 1
Try yourself:x, y and z are the three contestants in a kilometre race. If x can give y a start of 50 metres and x can also give z a start of 69 metres, then how many metres start can y give to z, if the race is supposed to end in a dead heat?
Explanation
Given, race is to end in a dead heat i.e. they are all supposed to cross the finish line at the same time.
Position of x from finish line = 1000
Position of y from finish line = 1000 - 50 = 950
Position of z from finish line = 1000 - 69 = 931
So, y can give a 19 m start to z for the given scenario to be true.
Report a problem
Question for Practice Questions Level 2: Speed, Time & Distance - 1
Try yourself:A train passes a 60 metres long platform in 20 seconds and passes a man standing on the platform in 16 seconds. The speed of the train is
Explanation
Report a problem
Question for Practice Questions Level 2: Speed, Time & Distance - 1
Try yourself:In a flat race of L metres, A beats B by x1 metres and C by x3 metres. C will beat B, if
Explanation
Distance covered by A is L metres to finish the race.
Then, distance covered by B = L - x1 metres
Distance covered by C = L - x3 metres
C beats B, if and only if the distance covered by C at that moment is greater than B.
So, (L - x3) > (L - x1)
Solving, x1 > x3.
Report a problem
Question for Practice Questions Level 2: Speed, Time & Distance - 1
Try yourself:Two trains starting from the same station and travelling in opposite directions are 227.5 km apart in 3 hours 15 min. Had they been travelling in the same direction, they would have been 32.5 km apart in the same time. Find their speeds (in kmph).
Explanation
When the trains are travelling in opposite direction, the sum of their speeds (relative speed) = (227.5/3.25) = 70 kmph
If they had been travelling in same directions, the difference of their speeds (relative speed) = (32.5/3.25) = 10 kmph
Hence, the speed of the faster train = (70 + 10)/2 = 40 kmph and the speed of the slower train = (70 - 10)/2 = 30 kmph
Report a problem
Question for Practice Questions Level 2: Speed, Time & Distance - 1
Try yourself:Javed wanted to reach the ground floor of the building. He went down at the rate of 1 stair in 1 minute. 16 minutes after he started, Salma started from the same point, from where Javed stared, to reach the ground floor of the building. She went down at the rate of 2 stairs in 1 minute. In how many minutes did Salma overtake Javed?
Explanation
Speed of Javed = 1 stair/min
After sixteen minutes, relative distance between Javed and Salma = 16 stairs
Speed of Salma = 2 stairs/min
Relative speed of Salma w.r.t. Javed = 2 - 1 = 1 stair/min
Time taken by Salma to cross Javed = 16/1 = 16 minutes
Report a problem
Question for Practice Questions Level 2: Speed, Time & Distance - 1
Try yourself:A man standing inside a tunnel notices that Train A is running inside the tunnel with a speed of 45 kmph. Another Train B, which is half the length of Train A and coming from opposite direction, is running at a speed of 81 kmph. Train A passes Train B in 4 seconds. Which of the following is the closest approximation of the length of the tunnel, if Train A passes completely through it in 4 minutes?
Explanation
Report a problem
Question for Practice Questions Level 2: Speed, Time & Distance - 1
Try yourself:A train of length 500 m crosses a platform in 50 sec and another train of the same length, moving in the opposite direction with double the speed of the first train, crosses a pole in 20 sec. What is the length of the platform?
Explanation
Assume length of platform = L metres
Speed of first train = V m/sec
According to the given condition,
50V = L + 500
Speed of second train = 500/20 = 25 m/sec
Therefore, speed of first train = 12.5 m/sec
Hence, length of platform = 50 × 12.5 - 500 = 625 - 500 = 125 m
Report a problem
Question for Practice Questions Level 2: Speed, Time & Distance - 1
Try yourself:Varun went for a long ride last Sunday. Every hour, he maintained a constant speed of 60 kmph. But after every 1 hour ride, he took rest for 10 minutes. If he starts from a place A at 8 a.m. and reaches a place B at 2 p.m. on the same day, what is the distance between A and B?
Explanation
Total time he travelled = 5 hours 10 minutes (∵ Varun rested for 50 minutes.)
So, d = 60 × 5 = 60 × 31/6 = 310 km
= 60 × 31/6 = 310 km
Report a problem


 = 770.9 km
= 770.9 km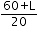 ........ (1)
........ (1)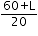
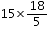 = 54 kmph
= 54 kmph