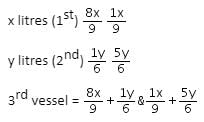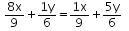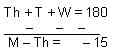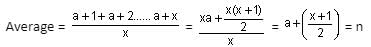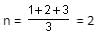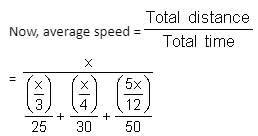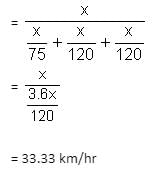This EduRev document offers 10 Multiple Choice Questions (MCQs) from the topic Averages (Level - 3). These questions are of Level - 3 difficulty and will assist you in the preparation of CAT & other MBA exams. You can practice/attempt these CAT Multiple Choice Questions (MCQs) and check the explanations for a better understanding of the topic.
Question for Practice Questions Level 3: Averages - 1
Try yourself:A shipping clerk has five boxes of different but unknown weights, each weighing less than 100 kg. The clerk weighs the boxes in pairs. The weights obtained are 110, 112, 113, 114, 115, 116, 117, 118, 120 and 121 kg. What is the weight of the heaviest box?
Explanation
Go with the options:
If 60 is the heaviest weight, to make 121, the second heaviest weight must be 61, which is not possible.
If 62 is the heaviest weight, the second heaviest weight will be (121 - 62) = 59
The third heaviest will be (120 - 62) = 58
Now, the lightest weight will be 112 - 58 = 54 ( Second least sum = Smallest + Third)
So, the second lightest weight must be 110 - 54 = 56
So, the weights are 54, 56, 58, 59 and 62.
We can make all the ten pairs from these.
Report a problem
Question for Practice Questions Level 3: Averages - 1
Try yourself:Two vessels contain mixtures of milk and water in ratios 8 : 1 and 1 : 5, respectively. The contents of both of these are mixed in a specific ratio into a third vessel. How much mixture should be drawn from the second vessel to fill the third vessel (capacity 26 gallons) completely in order that the resulting mixture may be half milk and half water?
Explanation
Let x litres of the first mixture be mixed with y litres of the second mixture.
Milk Water
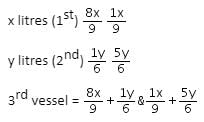
Since the third vessel contains half milk and half water;
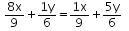
16x + 3y = 2x + 15y
14x = 12y
x/y = 12/14 = 6/7
Hence, y = 7 /(7+ 6) of 26 gallons = 7/13 x 26 = 14 gallons
Report a problem
Question for Practice Questions Level 3: Averages - 1
Try yourself:The average temperature on Monday, Tuesday and Wednesday was 55°C and that on Tuesday, Wednesday and Thursday was 60°C. Find the temperature on Monday, if the temperature on Thursday was 56°C.
Explanation
Total temperature for (M + T + W) = 3 × 55 = 165°C
Total temperature for (T + W + Th) = 3 × 60 = 180°C
On subtracting, we get
M + T + W = 165
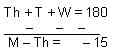
Th – M = 15
56 – M = 15
Temperature on Monday = 41°C
Report a problem
Question for Practice Questions Level 3: Averages - 1
Try yourself:The average of x consecutive integers is n and the average of the next y consecutive integers is n + 6. Find the relation between x and y.
Explanation
Let x consecutive numbers be a + 1, a + 2, ……… a + x.
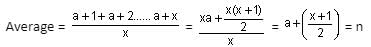
Next y consecutive numbers be a + x + 1, a + x + 2, …….. a + x + y.

2x + 1 + y = x + 1 + 12
x + y = 12
Alternative method:
Let 3 consecutive numbers be 1, 2 and 3.
Average,
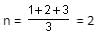
Next numbers be 4, 5, 6 ….
Average = n + 6 = 8
∴ Next numbers must be 4, 5, 6, 7, 8, 9, 10, 11 and 12.
Hence, y must be 9.
border=0 x + y = 3 + 9 = 12
Report a problem
Question for Practice Questions Level 3: Averages - 1
Try yourself:The average weight of 12 oil drums is 60 kg, which is equal to the difference between the weights of the two heaviest drums. If the average weight of the remaining 10 drums is half the total average weight, then find the weight of the heaviest drum.
Explanation
Average weight of 12 drums = 60 kg
Sum of weights = 12 × 60 = 720 kg
60 = H – Sv ...(1) [Where H and Sv are the weights of the two heaviest drums]
And, 1/2(60) = (Total weight of remaining 10 oil drums)/10
300 = Total weight of remaining 10 oil drums …(2)
It means that the sum of the remaining two drums is 420 kg.
H + Sv = 420 ……(3)
H – Sv = 60 ……(4)
2H = 480
H = 240 kg
Report a problem
Question for Practice Questions Level 3: Averages - 1
Try yourself:One hundred and twenty students take an examination with maximum 100 marks (with no fractional marks). No three students are awarded the same marks. What is the smallest possible number of pairs of students who are awarded the same marks?
Explanation
Total number of students = 120
Maximum marks of the exam = 100
∵ The fractional marking is not allowed, so there are 101 students who can get different marks from 0 to 100, remaining 19 students can also get the marks from 0 to 100.
∵ No three students can get the same marks, so there are 19 pairs of students who are awarded the same marks.
Report a problem
Question for Practice Questions Level 3: Averages - 1
Try yourself:A worker earned an average of $1500 per month from January to May. Then, he earned $2000, $2500, $2475 and $2325 during the months of June, July, August and September, respectively. He went on a vacation for the whole month of October. During November, he earned 100% more than what he earned in December. If his average earnings for the entire year was $1800, find his earnings in the month of November (in $).
Explanation
Average earning for the entire year = $1800
Total earnings in the year = $21,600
According to the question:
5 × 1500 + 2000 + 2500 + 2475 + 2325 + 0 + 2x + x = 21600 (where x is his earnings in December)
⇒ x = 1600
Earnings in November = 2x = $3200
Report a problem
Question for Practice Questions Level 3: Averages - 1
Try yourself:One-third of a certain journey was covered at a speed of 25 km/hr, one-fourth at a speed of 30 km/hr and the rest at a speed of 50 km/hr. Find the average speed for the whole journey.
Explanation
Let the total distance covered be x km.
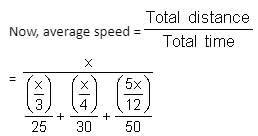
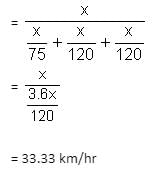
Report a problem
Question for Practice Questions Level 3: Averages - 1
Try yourself:A baseball team, which played 60 games, won 30% of its played games. After a phenomenal winning streak, this team raised its winning percentage to 50%. How many more games must the team have won in order to attain this average?
Explanation
30% of 60 = 18
If x more games were played by the team and all were won continuously, then
18 + x = 0.50(60 + x)
0.5x = 12
x = 24
Hence, 24 more games have to be won in order to attain this average.
Report a problem
Question for Practice Questions Level 3: Averages - 1
Try yourself:
Three groups A, B and C contain only the numbers 22, 26, 31 and 33 (assume enough copies of each exist to make every listed transfer feasible). You may perform any number of operations; each operation moves exactly five identical numbers from one group to another. Your goal is to obtain the minimum possible average of group A at the end.
Which of the following will definitely not be part of any sequence of operations that achieves that minimum for A?
Explanation
To minimize A’s average, you keep the smallest numbers in A. Since 22 is the smallest available value, moving 22s out of A can only increase (or fail to reduce) A’s average, so option C can never be part of an optimal sequence.
Report a problem